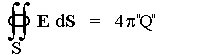Hmota z prázdnoty utvořená, topologická interpretace elektrického náboje

dodatek B
UNITÁRNÍ TEORIE POLE A KVANTOVÁ GRAVITACE
B.1. Proces sjednocování ve fyzice
B.2. Einsteinovy vize geometrické unitární teorie pole
B.3. Wheelerova geometrodynamika. Gravitace a topologie.
B.4. Kvantová geometrodynamika
B.5. Kvantování gravitačního pole
B.6. Sjednocování fundamentálních interakcí. Supergravitace. Superstruny.
B.7. Obecné principy a perspektivy unitární teorie pole

B.3. Klasická geometrodynamika. Gravitace a topologie.

V jistém smyslu pokračovatelem Einsteinových snah o vytvoření unitární teorie pole, avšak poněkud jinou cestou, se stal americký fyzik John Archibald Wheeler, který s dalšími spolupracovníky, především Ch.Misnerem, vyšel z původní (ověřené a osvědčené) Einsteinovy obecné teorie relativity. Ukázal, že k vytvoření klasické unitární teorie pole (a přitom dokonalejší než byly předchozí snahy) není třeba do obecné teorie relativity zavádět žádné umělé a neopodstatněné změny, stačí jen plně využít všech geometrických a topologických možností, jež obecná teorie relativity poskutuje.

V kapitole 2 jsme si ukázali, že obecná teorie relativity svrhla prostor a čas z postavení jakési nezúčastněné "scény", na níž se odehrávají fyzikální děje, a učinila prostoročas přímým účastníkem fyzikálního dění. Gravitační pole je podle OTR projevem křivosti prázdného prostoročasu - máme tedy jakousi "gravitaci bez gravitace".

Elektromagnetismus "bez elektromagnetismu"
Jak bylo ukázáno v §2.5, Einsteinovy rovnice gravitačního pole R_ik - ¹/₂ g_ikR= 8pT_ik mají tu důležitou vlastnost, že popisují chování nejen gravitačního pole, ale nepřímo - přes zákony zachování energie a hybnosti T^ik_;k = 0 - i jeho zdrojů. Vezmeme-li tedy elektromagnetické pole ve vakuu, pak z Einsteinových rovnic jím buzeného gravitačního pole

plynou i Maxwellovy rovnice tohoto elektromagnetického pole F^ik_;k = 0. Pokud je zakřivení prostoročasu způsobeno elektromagnetickým polem, potom stopa Einsteinova tenzoru na levé straně (B.7) musí být rovna nule, což dává R = 0 a dále kvadrát Ricciho tenzoru R^m_i R^k_m = d^k_i.(¹/₂ R_lmR^lm) je násobkem jednotkové matice.
  Einsteinovy a Maxwellovy rovnice (což jsou soustavy rovnic 2.řádu) se tedy dají sloučit do jedné soustavy rovnic 4.řádu - Einstein-Maxwellových rovnic, která v geometrickém tvaru obsahuje jak Maxwellovu elektrodynamiku (bez nábojů) v zakřiveném prostoročase, tak i Einsteinovy rovnice udávající zakřivení prostoročasu tímto elektromagnetickým polem *). Elektromagnetické pole zanechává na geometrii prostoročasu charakteristické "stopy", z nichž jej lze "poznat" a jejichž chováním je určeno. Elektromagnetické pole (které je takto určeno výrazem obsahujícím odmocniny Ricciho tenzoru křivisti R_ik) lze tedy plně popsat pomocí pouze gravitačních veličin, v konečném důsledku pomocí složek metrického tenzoru g_ik. Maxwellovy rovnice jsou pak dány vztahem mezi Ricciho křivostí a rychlostí, s jakou se tato křivost mění; zákony elektrodynamiky tak nabývají čistě geometrický charakter. Dostáváme jakýsi "elektromagnetismus bez elektromagnetismu", v němž elektromagnetické pole je projevem prázdného zakřiveného prostoročasu.
*) Ukázalo se však [281], že při integraci těchto Einstein-Maxwellových rovnic mohou příslušné okrajové podmínky (hodnoty g_ik a jejich časových parciálních derivací g_ik,0) na počáteční Cauchyově hyperploše x⁰=0 odpovídat současně více než jednomu Maxwellovskému poli, více hodnotám F_ik. Uvedená metoda geometrického popisu elektrodynamiky se tím v obecném případě stává nejednoznačnou...

Misner a Wheeler (s použitím dřívějších výsledků Rainicha pro elektromagnetické pole v OTR [213]) tedy dospěli k závěru, že již původní Einsteinova obecná teorie relativity v jistém smyslu splňuje to, oč se Einstein do konce života bezúspěšně snažil: jednotný popis gravitačního a elektromagnetického pole. A přitom popis zcela přirozený a nenásilný, při němž se dosavadní teorie nijak nemění.

Na začátku §B.1 jsme zdůraznili neuspokojivost koncepce, podle níž je pole buzeno zdrojem odlišným od pole. Pro elektromagnetické pole jako zdroj gravitace ve vakuu zde byla situace shora úspěšně vyřešena, aspoň v zásadě. "Materiálními" zdroji elektromagnetického pole jsou elektrické náboje. Geometrodynamika i zde navrhuje elegantní řešení: topologickou interpretaci elektrických nábojů pomocí jakýchsi "tunelů" v zakřiveném prostoru, které zachycují elektrické siločáry a efektivně se chovají jako elektrické náboje (viz níže "Topologická interpretace elektrického náboje").
  Zdrojem gravitace v klasické fyzice je především obecná, blíže nespecifikovaná a nestrukturovaná hmota - objekty (tělesa, částice) mající hmotnost. V předchozích unitárních teoriích se částice pokoušeli interpretovat jako nějaké zvláštnosti (singularity) v poli, což však vede k řadě potíží (srovnej §3.7), nebo jako nějaké spojité zhuštěné struktury mající své zákony vnitřního pohybu; tyto zákony vnitřního pohybu však byly zavedeny zvenčí a nebylo jasné, jak je odvozovat v rámci uzavřené teorie.
   Jinak je tomu v geometrodynamice. Vezmeme-li Schwarzschildovu geometrii v prázdném asymptoticky rovinném prostoročase, bude ve velkých vzdálenostech od středu platit obyčejný gravitační zákon stejně, jako kdyby ve středu byla reálná hmota. Jedná se tedy o prázdný zakřivený prostor, v němž působí gravitační přitažlivost, takže Schwarzschildova geometrie je nejjednodušším geometrodynamickým modelem "hmoty bez hmoty". Je to ale model s topologií odlišnou od eukleidovské a obsahuje singularitu (§3.4).

Hmota "bez hmoty"
G e o n y -
Zákony obecné teorie relativity však připouštějí existenci objektů s obvyklou eukleidovskou topologií a bez singularit, chovajících se jako skutečná hmota (budící gravitační pole i na toto pole reagující), přičemž tyto objekty jsou složeny čistě ze samotného pole. Šíří-li se prostorem elektromagnetické vlny, budí kolem sebe gravitační pole - zakřivují prostoročas v němž se šíří, a to nezůstává bez vlivu na jejich pohyb. Podle obecné teorie relativity mohou velmi mohutné elektromagnetické vlny kolem sebe vytvořit tak silné gravitační pole, že jím budou nuceny trvale se pohybovat po uzavřených dráhách. Elektromagnetické vlny si tak samy vytvářejí kolem sebe jakýsi gravitační "vlnovod" ze zakřivené geometrie prostoročasu (z gravitačního pole), v němž trvale cirkulují - obr.B.2a. Takový útvar z elektromagnetických vln, udržovaný pohromadě vlastní gravitací své energie pole, se nazývá (elektromagnetický) geon [284].

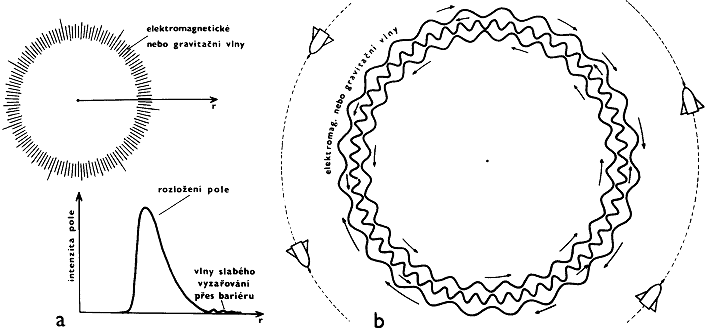
Obr.B.2. Mohutné elektromagnetické nebo gravitační vlny mohou kolem sebe vytvořit tak silné gravitační pole (zakřivit prostoročas), že jím budou trvale nuceny cirkulovat v uzavřeném "gravitačním vlnovodu" - vzniká metastabilní hmotný útvar geon. a) Průměrné rozložení pole v geonu.
b) Svými gravitačními účinky se geon chová jako každá jiná hmota (třebas planeta) - můžeme např. na oběžnou dráhu kolem geonu uvést družici.

Ke geonu je možno dospět např. následujícím myšleným pokusem: Mějme černou díru hmotnosti M, na jejíž fotonovou sféru r=3M (§4.3) budeme posílat mohutné dávky elektromagnetických vln. S rostoucím množstvím energie elektromagnetických vln obíhajících po fotonové sféře budou tyto vlny stále více přispívat k celkovému gravitačnímu poli které je tam udržuje, takže o příslušnou hodnotu můžeme zmenšit hmotnost černé díry (ve skutečnosti je to však zakázáno 2.zákonem dynamiky černých děr - viz §4.6). Při dostatečně velkém nahromadění elektromagnetických vln můžeme černou díru již zcela "odstranit" *), protože energie~hmotnost samotných vln již stačí vytvořit dostatečně silné gravitační pole aby udržovala samu sebe na "fotonové sféře" - udržovala cirkulaci vln v geonu.
*) Není však znám žádný mechanismus, jak odstranit (či postupně "řízeně odstraňovat") iniciační černou díru uvnitř geonu (pomineme-li hypotetický či sci-fi topologický tunel "červí díry" - srov. §4.4, pasáž "Červí díry - mosty do jiných vesmírů? Stroje času?"). Jedná se jen o umělý myšlený experiment. "Přirozeným" způsobem by geony snad mohly vznikat v mohutných primordiálních fluktuacích v Planckově času na počátku vesmíru..?.. - srov. §5.5 "Mikrofyzika a kosmologie. Inflační vesmír.".
  Jestliže geon celkové hmotnosti M bude sféricky symetrický, bude vzbuzovat sféricky symetrické gravitační pole a prostoročasová metrika bude (srovnej s §3.4)

ds²   =   - g_tt dt² + g_rr dr² + r²(dJ² + sin²J dj²)   .

Radiální složka metriky má obvyklý Schwarzschildovský tvar g_rr = 1/[1 - 2m(r)/r], kde m(r) je hmotnost~energie obsažená uvnitř koule o poloměru r. Časová složka metriky vně geonu má též Schwarzschildovský tvar g_tt = 1 - 2M/r, uvnitř geonu má hodnotu g_tt = 1/9 (čas uvnitř geonu plyne třikrát pomaleji než daleko od geonu). Geon není úplně stabilní, ale pouze metastabilní - část energie vln proniká přes odstředivou a gravitační bariéru, geon se pomalu rozplývá (tím pomaleji, čím větší je počet vlnových délek po obvodu), nebo naopak by mohl zkolabovat a vytvořit černou díru. Pro vzdáleného pozorovatele bude geon vykazovat gravitační účinky stejné jako každá jiná hmota (třebas planeta) - můžeme např. na oběžnou dráhu kolem geonu uvést družici (obr.B.2b).
  Taková hmota složená z elektromagnetických vln se nám může zdát sice zvláštní, avšak hmotná povaha elektromagnetických vln je dostatečně vžitá. Ještě sugestivnější obraz dostaneme, když nahradíme elektromagnetické vlny vlnami gravitačními. Gravitační vlny rovněž přenášejí energii (§2.7 a 2.8), zakřivují prostoročas (univerzální buzení gravitace) a podle obecné teorie relativity mohou též vytvořit "gravitační" geon, který se bude navenek svými gravitačními účinky projevovat jako skutečná hmota.
  Co jsou to však gravitační vlny? - jsou vlněním gravitačního pole, tedy fluktuacemi geometrie prázdného prostoročasu. Vnější pozorovatel se tak stává svědkem zajímavé věci: vlnící se křivost prázdného prostoročasu "bez hmoty" se bude jevit jako hmotný útvar! Gravitační geon je tedy názorným modelem jakési "hmoty bez hmoty", hmoty utvořené doslova z "prázdnoty" prostoru s vlnící se křivostí. Zde je třeba říci, že celá koncepce geometrodynamiky se setkává s určitými filosoficko-metodologickými problémy; neznamená to však, že by uvedené koncepce odporovaly základním postulátům materialistické filosofie *), která je přirozenou platformou fyziky a přírodovědy vůbec.
*) Sledujeme-li totiž hmotu buď ve stále menších měřítcích mikrosvěta, nebo naopak ve stále větších měřítcích megasvěta, bude hmota postupně ztrácet některé atributy na něž jsme zvyklí z běžné zkušenosti našeho makrosvěta a případně se začnou objevovat atributy nové. Vždy však zůstává základní znak hmoty - být objektivní realitou.

Hypotetický (modelový) geon je však jen určitým extrémním příkladem konstrukce hmotného objektu z geometrie prostoročasu; shora byly zmíněny některé principiální problémy s jeho vytvořením a se stabilitou geonu vůči vyzařování a rozptylu gravitačně uvězněných obíhajících vln-kvant elektromagnetického či gravitačního vlnění. Nesplnily se počáteční naděje, že by se geon snad mohl použít jako klasický model stabilních (elementárních?) částic. Je produktem klasické teorie pole a dokud nebude vybudována plně vyhovující kvantová teorie gravitace, nelze případný vztah mezi geony a kvantově-mechanickými elementárními částicemi blíže specifikovat. Není zatím naděje, že by snad mohly existovat nějaké "mikro-geony" stabilizované kvantovými efekty (nějak podobně jako orbity elektronů v atomových obalech jsou stabilizovány kvantovým kospuskulárně-vlnovým dualismem?), které by mohly modelovat elementární částice...
  Z teoretického hlediska ani nemusíme chodit k takovým složitým konstrukcím. Fakticky totiž každá gravitační vlna popsaná svým Isaacsonovým tenzorem nelokální energie-hybnosti (viz §2.8) je takovou "hmotou bez hmoty", složenou z "vakua" (chápaného v obvyklém smyslu). To, jak se i v "prázdném" prostoru bez obvyklých "reálných" hmotných zdrojů objeví jakási efektivní hmota mající globální gravitační účinky, je ostatně podobné situaci v elektrodynamice, kde se i ve vakuu bez přítomnosti elektrických nábojů (a proudů) pro nestacionární elektromagnetické pole objevuje Maxwellův posuvný proud mající magnetické účinky stejné jako "skutečný" proud elektrických nábojů...

Topologická interpretace elektrického náboje
Náboj "bez náboje"
Všimněme si nyní elektrických nábojů. Elektrické náboje (a jejich proudy) jsou zdroji elektromagnetického pole, avšak jsou zároveň čímsi "cizorodým" v teorii samotného elektromagnetického pole - jakási substance odlišná od pole. V místech kladných elektrických nábojů elektrické siločáry začínají a vycházejí na všechny strany, do míst záporných elektrických nábojů siločáry ze všech stran vstupují a tam končí (obr. B.3a); Maxwellovy rovnice pole zde neplatí. Celkový elektrický náboj v libovolné části prostoru lze podle Gaussovy věty zjistit tak, že vyšetřovanou oblast obklopíme (myšlenou) uzavřenou plochou S a změříme intenzitu E elektrického pole ve všech místech této uzavřené plochy - určíme "počet siločar" které jdou dovnitř nebo ven (obr. B.3a).

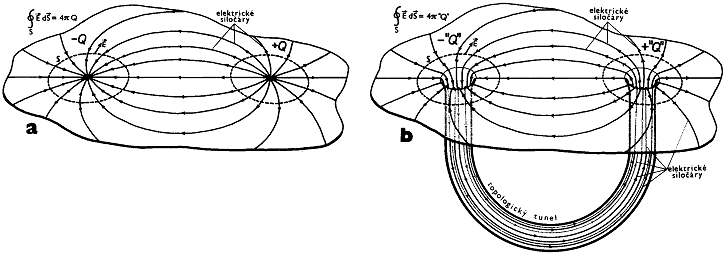
Obr.B.3. Klasická a topologická interpretace elektrických nábojů.
a) Obvyklé chápání elektrického náboje Q jako "substance"; z níž vycházejí (nebo do níž vcházejí) siločáry buzeného elelktrického pole.
b) Topologická interpretace elektrického náboje - neexistuje žádný "skutečný" náboj jako substance, siločáry nikde nezačínají ani nekončí, jsou jen zachyceny a procházejí topologickým tunelem, jehož hrdla se pak jeví jako "zdánlivé" náboje "Q".

Nemohou se však siločáry, které jdou dovnitř, nějak "nepozorovaně" dostat zase ven aniž bychom to zaznamenali na uzavřené ploše tento vnitřek ohraničující (nebo podobně siločáry jež jdou ven se dostat zpět dovnitř)? Na první pohled se taková otázka zdá být absurdní. Uzavřeme-li přece někoho ze všech stran do vězení, je podle zdravého rozumu nemyslitelné, aby se dostal ven aniž by musel projít stěnou svého vězení - probourat zeď, otevřít v ní dveře.
  Nakresleme si tuto situaci v dvojrozměrném případě na kus papíru; místo lidí si mysleme mravence, které zde budeme považovat za dvojrozměrné bytosti (obr.B.4). Na obr.B.4a má dvojrozměrný svět mravenců obvyklé vlastnosti a vězeň nacházející se uvnitř uzavřené křivky se skutečně nijak nemůže dostat ven aniž by prošel touto hranicí svého vězení.

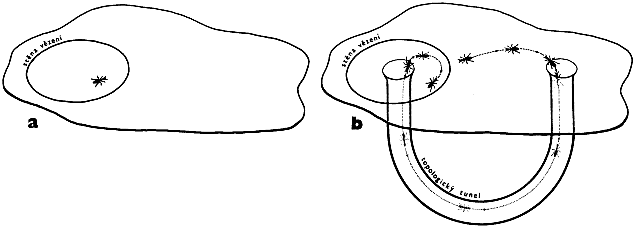
Obr.B.4. Vliv topologických vlastností prostoru na možnosti pohybu.
a) Vězeň (mravenec) obklopený ze všech stran stěnou vězení se v prostoru (zde dvojrozměrném) s obvyklými topologickými vlastnostmi nijak nemůže dostat ven, aniž projde stěnou vězení.
b) V prostoru s vícenásobně souvislou topologií lze opustit uzavřené vězení bez nutnosti projití jeho stěnou. Mravenec může projít topologickým tunelem a podívat se zvenku na neporušenou stěnu svého vězení.

Co však když dvojrozměrný svět mravenců vypadá topologicky tak, jak je to znázorněno na obr. B.4b? Mravenec uvězněný v oblasti ze všech stran obklopené uzavřenou křivkou (stěnou vězení) může projít "tunelem" a podívat se zvenku na svoje vězení bez toho, že by musel projít v některém místě uzavřenou stěnou svého vězení. Z hlediska trojrozměrného okolí, do něhož je tato konstrukce vnořena, na tom není nic divného - mravenec, i když se pohybuje stále v rámci své dvojrozměrné plochy (svého světa), "podleze" stěnu svého vězení tak říkajíc přes "další rozměr". Z hlediska samotných dvojrozměrných mravenců, pro které žádný "třetí rozměr" neexistuje, se však stal jakýsi zázrak: vězeň ze všech stran obklopený zdí se najednou odněkud zvenku přišel podívat na neporušenou stěnu svého vězení! Příčina je v tom, že uvedený dvojrozměrný prostor má jiné topologické vlastnosti než na obr.B.4a. Je vícenásobně souvislý. Uzavřená křivka zde již nemusí být hranicí oblasti uvnitř! Lokální geometrické vlastnosti v každém místě přitom mohou být zcela obvyklé (jen mírné zakřivení).

Nyní se již můžeme opět vrátit k elektrickým nábojům. Na obr.B.3a je obvyklým způsobem v dvojrozměrném nákresu znázorněn kladný a záporný elektrický náboj - z kladného náboje siločáry vycházejí (podle dohody) a končí na záporném náboji. Obklopíme-li náboj myšlenou uzavřenou plochou S, můžeme "spočítáním" siločar jež vcházejí nebo vycházejí stanovit hodnotu náboje Q uvnitř. Tam však žádný "skutečný" elektrický náboj nemusí být! Při vhodné topologii prostoru, jak je znázorněno na obr.B.3b, sice budou uzavřenou plochou S siločáry vstupovat dovnitř, tam však nebudou končit, ale topologickým "tunelem" projdou do jiného místa prostoru, odkud budou zase vycházet a vracet se zpět. Vnějšímu pozorovateli, který bude měřit elektrické pole, se jedno "ústí tunelu" bude jevit jako záporný náboj -"Q" (siločáry jdou dovnitř) a druhé hrdlo tunelu jako kladný náboj +"Q" (siločáry jdou ven). Elektrické pole, jehož siločáry procházejí topologickým tunelem, všude vyhovuje Maxwellovým rovnicím. V důsledku toho se celkový tok intenzity elektrického pole přes ústí tunelu nemůže měnit s časem, pokud se nemění topologie; nezáleží přitom na proměnnosti elektromagnetického pole, zakřivení prostoru, změnách "průřezu" topologického tunelu ani vzdálenosti obou jeho ústí. Tok elektrického pole každou uzavřenou plochou S obklopující tunel

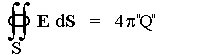
tedy vyhovuje zákonu zachování elektrického náboje a Gaussově větě elektrostatiky.

Taková topologická interpretace elektrického náboje je vlastně "nábojem bez náboje": žádné "skutečné" elektrické náboje zde neexistují, elektrické siločáry nemají začátky ani konce, jsou pouze zachyceny a procházejí topologickým tunelem prostoru, jehož jednotlivá ústí se pak jeví jako kladné a záporné náboje "Q". Tedy volné elektromagnetické pole ve vakuu bez nábojů může vlivem vhodné topologické struktury prostoru vytvářet (efektivní) elektrické náboje. Elektrický náboj se v této teorii objevuje jako nelokální vlastnost elektrodynamiky (bez zdrojů) ve vícenásobně souvislém prostoru.

B.2. Einsteinovy vize geometrické unitární teorie pole		B.4. Kvantová geometrodynamika

Vojtěch Ullmann