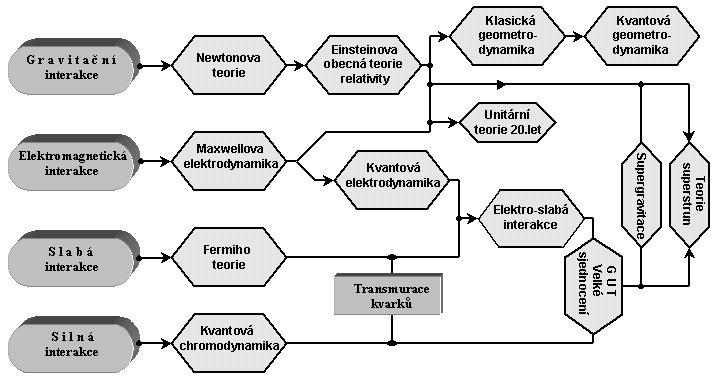
Obr.B.8. Schématické znázornění základní struktury sjednocování fundamentálních interakcí.
| AstroNuklFyzika ® Jaderná fyzika - Astrofyzika - Kosmologie - Filosofie | Gravitace, černé díry a fyzika |
dodatek B
UNITÁRNÍ TEORIE
POLE A KVANTOVÁ GRAVITACE
B.1. Proces sjednocování ve fyzice
B.2. Einsteinovy vize geometrické
unitární teorie pole
B.3. Wheelerova geometrodynamika.
Gravitace a topologie.
B.4. Kvantová geometrodynamika
B.5. Kvantování gravitačního
pole
B.6. Sjednocování fundamentálních interakcí. Supergravitace.
Superstruny.
B.7. Obecné principy a perspektivy
unitární teorie pole
B.6. Sjednocování
fundamentálních interakcí.
Supergravitace. Superstruny.
Objektivní důvod,
proč se A.Einsteinovi ani jeho následovníkům, přes
veškerou erudici a úsilí, nemohlo podařit vytvořit
uspokojivou unitární teorii pole, spočíval hlavně v tom, že
neměli k dispozici dostatečné experimentální údaje o zákonitostech mikrosvěta - o vlastnostech elementárních
částic. Snažili se takříkajíc "vymyslet
přírodu od psacího stolu". Částečně to platí i o
Wheelerově kvantové geometrodynamice popsané v §B.4, která
sice zavádí kvantový princip, ale jinak též uvažuje
vlastnosti pouze dvou druhů polí - gravitačního a
elektromagnetického.
Nyní je situace diametrálně odlišná.
Existuje obrovské množství experimentálních dat o
interakcích mnoha druhů elementárních částic při
nejrůznějších energiích. Z těchto experimentálních
údajů byly odvozeny důležité obecné principy, které je
třeba vzít v úvahu při sestavování každé unitární
teorie, jež si chce činit nárok na adekvátní popis
skutečnosti (§B.7). Vedle gravitačních a elektromagnetických interakcí se objevují další
dva typy interakcí hrající fundamentální úlohu v
mikrosvětě: silná interakce umožňující existenci jader
atomů a interakce slabá způsobující např.
radioaktivní b-rozpad.
Sjednocování 4 druhů interakcí
Rozsáhlé výzkumy v oblasti jaderné a částicové fyziky
vyústily v tzv. standardní model částicové
fyziky, v němž 25 fundamentálních částic a 4 síly
(interakce) dávají perfektně fungující vysvětlení
pro všechno v přírodě a vesmíru - viz §1.5, pasáž "Standardní model - jednotné chápání
elementárních částic"
v monografii "Jaderná fyzika a fyzika
ionizujícího záření".
Přesto však ani s tímto velkým úspěchem fundamentální
fyzika není spokojena. Jednak z fundamentálního pohledu 4
různé interakce jsou trochu "moc",
měla by být jen jedna! - aby bylo dosaženo
tzv. "teorie všeho" TOE (Theory Of Everything). A
další problém: jedna z fundamentálních sil - gravitace
- se zásadně liší od ostatních tím, že se
pro ni zatím nepodařilo vytvořit zcela konzistentní kvantovou
teorií (bylo diskutováno výše v §B5
"Kvantování gravitačního pole")...
Odlišné
vlastnosti gravitace
Nelinearita gravitace v OTR, "samogravitace",
zakřivování prostoročasu, jsou vlastnosti hodně odlišné od
ostatních druhů interakcí. To je patrně ta hlavní gnoseologická
překážka v úplné unitarizaci. . Někteří odborníci, zvláště v
kvantové fyzice, zde ještě akcentují (asi neodůvodněně) tzv. informační paradox u
černých děr (tato
problematika je diskutovatována v pasáži "NavratHmotyKvantEvaporaci"). Tato kontradikce kvantové fyziky a
obecné teorie relativity je zde (podle mého názoru) umělá a neopodstatněná, je to jen
subjektivní názor některých odborníků...
Moderní unitarizační snahy probíhají
na půdě kvantové teorie polí a jejich cílem je sjednocování fundamentálních interakcí mezi elementárními částicemi
- interakcí silných, slabých, elektromagnetických a
gravitačních. Protože se jedná o velmi rozsáhlou oblast
ležící většinou úplně mimo zaměření této knihy,
shrneme jen zcela heslovitě základní principy a poznatky
unitarizace ve fyzice elementárních částic - viz obr.B.8,
který je pokračováním základního unitarizačního schématu
z obr.B.1. Před rozebíráním konkrétních metod unitarizace
si však stručně přiblížíme základní ideje sjednocování polí a důležitou úlohu, jakou zde
hrají symetrie a zákony zachování.

Obr.B.8. Schématické znázornění
základní struktury sjednocování fundamentálních interakcí.
Fyzikální
pole « fyzikální
prostor ® sjednocení
Již v §B.2 jsme si nastínili velmi hlubokou a krásnou
myšlenku unitární teorie pole: podle ní by mělo existovat jediné,
zcela základní a vše zahrnující fyzikální pole, jehož
projevem by pak byla všechna pozorovaná pole v přírodě -
gravitační, elektromagnetické, pole silných a slabých
interakcí (a všechny jejich projevy, třebas v
subnukleární fyzice). Ve světě pak neexistuje nic než toto
pole, z něhož je všechno složeno - i hmotné útvary (např.
částice) jsou jakési místní "zhuštěniny" tohoto
pole.
Fyzikální pole
je prostor, v němž je určitým způsobem rozložena
(rozprostřena, distribuována) určitá veličina - v každém
bodě je definován určitý skalár, vektor či tenzor
popisující dané pole (potenciál či silové působení).
Časová evoluce (proměnnost) pole je v klasické fyzice
vyjádřena funkční závislostí veličin pole na čase, v
teorii relativity zavedním 4-rozměrného prostoročasu. V
daném prostoru může být přítomno více druhů polí, což v
klasickém přístupu vyjadřujeme pomocí několika vektorů či
tenzorů v každém bodě prostoru.
Chceme-li sjednotit
tato pole do jednoho unitárního pole, můžeme
z hlediska vztahu prostoru a pole postupovat v zásadě dvěma
způsoby :
Oba tyto způsoby mohou být do určité míry ekvivalentní, avšak existence velmi propracovaného matematického aparátu diferenciální geometrie a topologie variet upřednostňuje druhý přístup, který bude níže aplikován na geometrické formulace supergravitace a na teorii superstrun.
Symetrie
ve fyzice
Pojem symetrie ve
fyzice se vyvinul ze symetrií v
geometrii (a obsahuje tyto geometrické symetrie jako
důležitý speciální případ). V geometrii symetrie
vyjadřují pravidelnost tvaru určitých geometrických
útvarů. Máme zde centrální symetrii kruhu
nebo koule, axiální symetrii (osovou
souměrnost) válce, chirální symetrii -
zrcadlovou levo-pravou souměrnost. Symetrie geometrického
útvaru se projevuje tím, že při určitých změnách polohy
jeho jednotlivých bodů - tzv. transformacích,
se vlastnosti studovaného geometrického objektu nemění - jsou
vůči těmto transformacím invariantní.
Ve
fyzice to nemusí být taková jednoduchá a názorná symetrie,
ale může se jednat i o určité abstraktní symetrie
na úrovni matematických rovnic.
Symetrie a její
narušení
Na úrovni základních jevů a zákonitostí se příroda jeví
jako v zásadě symetrická, avšak jevové
úrovni bývá symetrie více či méně porušená.. Můžeme si
to názorně přiblížit na jednoduchém příkladu z běžného
života: když na stole postavíme tužku přesně kolmo na
špičku, je díky rotační (válcové) symetrii stejně pravděpodobné, že
spadne na jakoukoli stranu. V případě že by padala
přednostně na jednu stranu, znamenalo by to že symetrie
je narušena (mohlo by to být
způsobeno nehomogenitou materiálu tužky, drobnou odchylkou od
válcového tvaru, nesymetrickým seříznutím hrotu; příp.
vnějšími vlivy jako je přítomnost elektrického pole,
proudění vzduchu v místnosti a pod...).
Když k takovým narušením symetrie dochází v
oblasti částicových interakcí, indikuje to
přítomnost určitého pole způsobujícího
tuto asymetrii a též existenci nějaké nové částice,
která je kvantem toho pole; toto pole lze též chápat jako
"kompenzující" pole
potřebné k zachování základní symetrie, která se na
jevové úrovni zdá být narušená.
Symetrie
a zákony zachování
Ve fyzice se pod symetrií určitého fyzikálního systému
rozumí neměnnost (invariance) důležitých
vlastností tohoto systému při transformacích proměnných
veličin, které jej popisují. Velmi důležitou úlohu zde
mají především symetrie pohybových
rovnic,
popisujících dynamiku systému, vůči transformacím jejich
proměnných. Tedy takové transformace veličin popisujících
daný fyzikální systém, které ponechávají tvar pohybových
rovnic tohoto systému beze změn. Tyto symetrie pak mohou (ale
nemusí*) vykazovat i řešení těchto rovnic.
*) Rovnice popisující dynamiku systému
mají určité symetrie, avšak výsledný stav systému, který
je řešením těchto rovnic, tuto symetrii nerespektuje - např.
v důsledku nesymetrických počátečních podmínek.
Podle teorému E.Noeterové invariance
pohybových rovnic vůči určitým transformacím vede k zákonům zachování určitých fyzikálních
veličin. V klasické mechanice lze zákon zachování energie
považovat za důsledek homogenity
času
(nezávislost na posunu v čase), zákon zachování hybnosti za
důsledek homogenity prostoru (invariance vůči prostorovým
translacím) a zákon zachování momentu hybnosti za důsledek izotropie prostoru (symetrie vůči prostorovým rotacím).
Prvním důležitým principem symetrie v
moderní fyzice byla Lorentzovská
invariance,
původně objevená jako (víceméně náhodná) matematická
vlastnost Maxwellových rovnic odvozených z experimentálně
pozorovaných zákonů elektromagnetismu. Tehdejší chod
fyzikálních úvah byl zhruba následující :
| experiment | ® | rovnice pole | ® | symetrie . |
Zásluhou A.Einsteina a jeho teorie relativity si fyzikové uvědomili, že principy symetrie mohou být mocným gnoseologickým nástrojem; vzpomeňme si jen, že právě z požadavku symetrie vůči obecným transformacím prostoročasových souřadnic, spolu s principem ekvivalence, vyplynula obecná teorie relativity. Nyní je metodou teoretické fyziky spíše schéma :
| principy symetrie | ® | lagrangián | ® | rovnice pole |
Fyzikálně odůvodněný požadavek určité symetrie může sloužit jako určitý "konstrukční princip" či pomůcka při vytváření fyzikálních teorií a modelů. A přítomnost symetrií ve fyzikálních modelech umožňuje vyvozovat některé důležité teoretické předpovědi, aniž musíme znát konkrétní podrobné (a často značně složité) řešešní pohybových rovnic.
Kalibrační (cejchovací)
transformace; kalibrační pole
Termín kalibrace *) či cejchování
ve fyzikálních, technických a laboratorních oborech značí
proceduru, při níž se provádí či ověřuje přesné
nastavení vztahu mezi měřenými veličinami na
měřicích přístrojích či pomůckách. Typickým
jednoduchým příkladem je kalibrace odměrného válce na
kapaliny, který se opatří značkami (čárkami, ryskami) s
vyznačeným objemem [mililitry]. Nebo kalibrace voltmetru,
který se opatří stupnicí s vyznačenými dílky hodnot
napětí [V, mV]. Kalibrace se provádí většinou
srovnáváním s hodnotami z jiných (přesnějších)
měřicích přístrojů a etalonů. Přesným kalibrováním se
zabývá speciální obor metrologie.
*) Slovo "kalibrace,
kalibr" pochází z Franc. caliper =
vnitřní průměr hlavně pušky či děla, vrtání, ráž
střelné zbraně. Přeneseně - něco co má určitou velikost,
průměr, přesné nastavení, cejchování.
Zde v teorii pole se jako kalibrace
přeneseně myslí takové vhodné nastavení - transformace,
"kalibrace" - určitých veličin (souřadnic,
potenciálů pole), které zachovává hodnoty intenzity pole,
ale přitom umožňuje vhodnější matematický zápis a
snadnější konkrétní řešení v teorii pole. Tato určitá
"svoboda" ve volbě potenciálů umožňuje vybrat tvar
potenciálů - provést jejich "kalibraci" tak, aby to
bylo co nejvýhodnější pro daný problém. Invariance polí
vůči kalibračním transformacím se nazývá kalibrační
invariance.
S tímto postupem jsme se v
naší knize již setkali např. v §1.5, pasáž
"Vlastnosti Maxwellových rovnic" - "Potenciály
pole", §2.5 "Einsteinovy rovnice gravitačního
pole", pasáž "Linearizovaná teorie gravitace" a
§2.7 "Gravitační vlny", pasáž "Rovinné
gravitační vlny v linearizované gravitaci".
Tuto klasickou koncepci invariance vůči
kalibračním transformacím [Lagrangián --> rovnice pole
--> transformace potenciálů zachovávající rovnice pole],
současné postupy budování unitárních teorií pole převracejí
naopak : požadavek invariance vůči určité kalibrační
transformaci se deklaruje za primární a z jeho
splnění se vyvozují vlastnosti polí. Při požadavku
lokální kalibrační invariance vůči specifickým (fyzikálně více či méně odůvodněným) symetriím se
v rovnicích pole objevují určité přídavné členy
obsahující derivace parametrů transformace, pro jejichž
eliminaci je potřeba zavést odpovídající kompensující
členy, které je možno interpretovat jako nějaké pole -
vzniká tím nové kalibrační pole, které by mohlo popisovat novou další interakci..?.. Bude
podrobněji rozebíráno níže. Z fyzikálně-filosofického
hlediska je to možná diskutabilní přístup, ale "funguje
to"...
Složením dvou transformací, při kterých se systém nezmění, vzniká rovněž operace zachovávající systém stejný - z matematického hlediska je tedy množina všech symetrií daného systému grupou :
Grupy transformací
Pro lepší pochopení některých níže používaných pojmů a
označení, typických pro unitární teorie pole, bude
užitečné vložit sem krátkou matematickou vsuvku s
nastíněním popisu transformací pomocí teorie grup.
Grupa je taková (neprázdná) množina G,
mezi jejímiž prvky je definována binární operace
"l" přiřazující každým dvěma prvkům a,bÎG nový prvek c =
albÎG, který je
rovněž prvkem G. Tato binární transformace je asociativní:
(alb)lc = al(blc), má jednotkový prvek iÎG: ali = ila = a pro každý prvek aÎG, a ke každému
prvku aÎG existuje prvek inverzní a-1ÎG: ala-1=a-1la= i.
Nejobvyklejším příkladem grupy je množina všech kladných
racionálních čísel při obvyklé operaci násobení ("l" = "."). Jestliže binární
operace "l" je komutativní, tj. alb = bla pro každé prvky a,bÎG, nazývá se G Abelova
grupa. Počet prvků g grupy G se nazývá řád
grupy. Jestliže je g nekonečné, ale spočetné, nazývá
se G nekonečná diskrétní grupa.
Pokud prvky grupy tvoří kontinuální množinu, řád grupy
již není použitelný. Zato lze do spojité množiny prvků
grupy zavést určité topologické vlastnosti
definující varietu (o topologii viz
podrobněji §3.1 "Geometricko-topologické vlastnosti"), popř. i metriku. Shora zavedenou binární
operaci c = alb, definující grupu, lze pak zapsat jako funkční
vztah c = f(a,b). Jestliže všechny tyto grupové operace
(indukující zobrazení grupy G samé na sebe) jsou spojité,
množina G tvoří topologickou grupu.
Topologická grupa, která je varietou, se nazývá Lieova
grupa *). Typickým příkladem Lieovy grupy je
Eukleidův prostor Rn. Rovněž množina spojitých transformací tvoří
Lieovu grupu. Právě grupy transformací, při
nichž se zachovávají určité veličiny, hrají důležitou
úlohu ve fyzice polí a částic. Jelikož fyzikální
transformace jsou matematicky vyjádřeny maticemi
transformačních koeficientů (Aij,Aab), příslušné grupy transformací jsou maticové
grupy.
*) Množiny tohoto druhu, které jsou
zároveň grupami i varietami, poprve zavedl v 70.letech 19.stol.
norský matematik Sophus Lie (1842-1899) při analýze
vlastností řešení diferenciálních rovnic. Lieovy grupy v
sobě spojují struktury ze tří základních matematických
oblastí: algebry, analýzy a geometrie. Používají se při
řešení diferenciálních rovnic, v diferenciální geometrii a
algebraické topologii, v kvantové mechanice, v teorii
relativity, při popisu interakcí částic, unitárních
teoriích pole (supergravitace, superstruny - viz níže). Ve
fyzikálních aplikacích většinou vystupují jako Lieovy
grupy symetrií studovaného systému.
Unitární grupa U(N) je definována jako
grupa všech transformací x'a = Aabxb (a,b=1,2,....,N), která zachovává skalární součin a
invarianci unitární délky vektoru |x| = x*axa - tj.
pro transformační matici platí vztah A*abAba = 1 (hvězdička* značí složku komplexně
sdruženou). Platí-li další omezení Det
A = 1, jedná se o tzv. unimodulární
podgrupu SU(N) grupy U(N).
................
..........
Grupy
ve fyzice
Ve fyzice našly grupy své první uplatnění v krystalografii,
kde se pomocí nich vyjadřují vlastnosti symetrie krystalové
mřížky pevných látek. V relativistické fyzice se poprvé
grupy objevily již v práci H.Poincaré, který ukázal, že
Lorentzovy transformace prostorových a časových souřadnic
mezi inerciálními vztažnými soustavami tvoří (Lieovu)
grupu; tato grupa obecných Lorentzových transformací
(nehomogenních, včetně translací) se nazývá Poincarého
grupa. Při dalším rozvoji speciální a zvláště
obecné teorie relativity se však s použitím grup můžeme
setkat jen ojediněle a okrajově. Teorie grup se od konce 20. a
začátku 30.let začala více uplatňovat v kvantové mechanice
při analýze víceelektronových konfigurací atomů a v
kvantové chemii.
Grupy unitární
symetrie
Nové obzory pro aplikaci grup se od 40. a 50.let let otevřely v
jaderné fyzice při popisu vlastností elementárních
částic. Velký počet elementárních částic, které
byly objeveny při vysokoenergetických interakcích, přirozeně
vedl ke snahám o jejich systematiku a zavedení
unitarizačních schémat. Především,
každému baryonu a leptonu je přiřazeno baryonové
číslo B a leptonové číslo L
(částice +1, antičástice -1), které se zachovávají při
všech interakcích. Byly zjištěny výrazné podobnosti
a symetrie mezi některými elementárními
částicemi, především hadrony.
Odhlédneme-li od elektrického náboje, lze např. protony a
neutrony považovat za dva stavy (dublet) jedné částice -
nukleonu. Podobně piony p+,po,p- tvoří triplet
podobných částic. Při studiu samotných silných interakcí,
které jsou nábojově nezávislé, můžeme od náboje
odhlédnout. Pro popis těchto podobností a symetrií byla
zavedena nová veličina izotopický spin neboli
izospin T *). Nukleony mají izospin T = 1/2,
přičemž projekce izospinu T = +1/2 odpovídá protonu a T =
-1/2 neutronu. Pionům se připsal izospin T = 1, s projekcemi
-1,0,+1 pro p-,po,p+. V soustavě
interagujících nukleonů a pionů pak platí zákon zachování
izospinu. Pro vyjádření těchto symetrií vznikla grupa SU(2)
- speciální, unitární (unimodulární) grupa v komplexním
2-rozměrném prostoru; tato grupa je lokálně izomorfní grupě
rotací O(3) v 3-prostoru, vyjadřující izotropii prostoru -
symetrii vůči prostorovým rotacím, vedoucí k zákonu
zachování momentu hybnosti.
*) Vyšlo se z formální analogie s
obyčejným spinem, kde částice se spinem 1/2 se vyskytuje ve
dvou stavech s průmětem spinu -1/2, +1/2 a částice se spinem
1 ve třech stavech s průměty spinu -1,0,+1. Izospin T
je vektorem v myšleném (pomocném) "izotopickém
prostoru". Obecně částice s izospinem T se může
vyskytovat v (2 T +
1) stavech s projekcemi izospinu na vztažnou osu: -T, (-T+1),
(-T+2), ..., -1, 0, 1, ..., (T-2), (T-1), T.
Dalším důležitým krokem byl objev některých
"podivných" (nečekaných) vlastností interakcí
mesonů K a hyperonů při jejich sdružené párové produkci,
které vedly k zavedení pojmu podivnosti,
popsaného kvantovým číslem S ("Strange").
Později bylo zavedeno obecnější kvantové číslo zvané hypernáboj
Y = B + S, dané součtem baryonového čísla B a
podivnosti S. Ukázalo se, že při silných interakcích
se zachovává jak izospin T, tak hypernáboj Y. To přivedlo k
hledání grupy SU(2)´Y, popisující rozšířené vlastnosti symetrie
hadromů. V r.1964 navrhli M.Gellman a E.Neeman použít
minimální Lieovu grupu, obsahující SU(2)´Y jako podgrupu - grupu
unitární symetrie SU(3). Tato rozšířená symetrie
vedla k sestavení multipletu baryonů - dekupletu (3/2+), v němž však v
té době chybělo jedno místo; byl tak předpovězen hyperon W, který byl
zanedlouho skutečně objeven.
Grupa symetrií hadronů je 4-parametrická grupa zachování
izospinu a hypernáboje. Další analýza unitární symetrie
ukázala, že systematiku hadronů lze velmi dobře vysvětlit
hypotézou, že hadrony jsou složeny ze subčástic - tripletu
kvarků ........ Vznikla tak kvarková chromodynamika jakožto
teorie silných interakcí .........
........
.........grupy symetrií U(1), SU(2), SU(3), ....., SO(...),
...., Lieovy algebry...
............
V terminologii teorie grup unitárních symetrií lze říci,
že částice jsou reprezentacemi grupy symetrií.
Přesněji, komponenty báze ireducibilní reprezentace grupy
symetrie ztotožňujeme (interpretujeme, přiřazujeme) s
množinou fyzikálních stavů - částicemi (popř. jejich
ecxitovanými stavy, rezonancemi).
Globální a lokální symetrie;
Kalibrační pole
Při studiu fyzikálních systémů si příslušné symetrie
můžeme rozdělit na čtyři kategorie. Podle vztahu [systém]-[okolí] se může
jednat o :
¨ Vnější symetrie - invariance vůči změnám
"pozice" systému (nebo jeho částí) v prostoru a
čase (vedle obvyklých transformací
prostoročasových souřadnic je to např. obrácení času
"T", nebo prostorová inverze "P");
¨ Vnitřní symetrie - invariance vůči
transformacím vnitřních charakteristik systému (např. výměna částic za antičástice, nábojové
sdružení "C").
Z hlediska prostoročasového
"rozsahu", konstantnosti či proměnnosti
transformací, se ve fyzice uplatňují symetrie dvojího druhu :
Základním východiskem kalibračních teorií je
theze, že všechny čtyři základní interakce v přírodě
jsou důsledkem požadavku invariance teorie vůči
příslušným kalibračním transformacím. V rámci
kalibrační teorie lze formulovat kvantovou elektrodynamiku (kde
elektromagnetické pole se obdrží jako kalibrační pole při
požadavku invariance lagrangiánu volného spinorového pole
vůči lokálním transformacím fáze z grupy
U(1)) i Einsteinovu gravitační teorii (gravitační
pole zde vzniká z požadavku invariance vůči lokálním
kalibračním transformacím prostoročasu - Poincaréova grupa).
Kalibrační pole v kalibračních
teoriích jsou primárně "nehmotná" (jejich kvanta mají nulovou
klidovou hmotnost), což je adekvátní pro pole
elektromagnetické a gravitační. Při budování teorie např.
slabých interakcí v rámci kalibračních teorií to však
způsobuje určité potíže pramenící z toho, že tyto
interakce jsou zprostředkovány intermediálními bosony (W+,W-,Z°), které mají díky krátkému
dosahu interakce značně velkou hmotnost (desítky GeV/c2).
Tuto potíž se podařilo překlenout mechanismem tzv. spontánního narušení symetrie [131],[153], což je modifikace
lagrangiánu, při níž sice lagrangián i pohybové rovnice
mají nadále původní danou symetrii, ale vlastní fyzikální
stavy tuto symetrii již nemají (není v tom žádný rozpor-
např. pohyb v centrálně symetrickém poli nemusí být při
nesymetrických počátečních podmínkách vůbec symetrický).
Toto spontánní narušení symetrie pak způsobuje, že příslušné
kalibrační pole bude efektivně vystupovat jako pole s
nenulovou hmotností, aniž by se porušila kalibrační
invariantnost.

Obr.B.9. Znázornění mechanismu spontánního narušení
symetrie v kalibračních teoriích.
a) Pro efektivní potenciál tvaru
jednoduché symetrické jámy s jediným minimem je i základní
stav symetrický.
b) Pro takový tvar
symetrického efektivního potenciálu základní stav pole j již
symetrii nemá.
c) Pohyb
kuličky puštěné přesně po ose do sklenice s promáčknutým
dnem ilustruje případ, kdy navzdory tomu, že rovnice pohybu
kuličky, počáteční podmínky i tvar sklenice jsou
symetrické, konečný stav tuto symetrii nemá: kulička se po
dopadu do metastabilní polohy ve vyvyšeném středu dna vždy
skutálí do prohlubně u stěny - předchozí symetrie se spontánně naruší.
Podstata mechanismu
spontánního narušení symetrie je zhruba nastíněna na
obr.B.9. Na obr.B.9a je znázorněna potenciální energie
(efektivní potenciál) skalárního pole j o hmotnosti m a
vazbové konstantě l s jednoduchým (modelovým)
lagrangiánem L = (1/2) (j,i)2 - (m2/2) j2 - (l/4) j4. Efektivní potenciál V(j) = (m2/2)
j2 - (l/4) j4 má (pro m2>0) tvar symetrické
potenciálové jámy, v níž nejvýhodnější energetický stav
odpovídá poli j =0. V případě, že efektivní potenciál by měl tvar V(j) = -
(m2/2) j2 - (l/4) j4 (odpovídající případu m2<0),
bude mít potenciálová jáma tvar podle obr.B.9b, takže minimu V(j) již nebude odpovídat stav j =0, ale pole j = jo = ±m/Öl . I když potenciál V(j) je nadále symetrický vůči změně
znaménka j ® -j,
zakladní stav pole j tuto symetrii již nerespektuje
(kulička symbolicky představující stav pole se vždy skutálí do
jednoho z minim - obr.B.9c).
Po narušení symetrie se spektrum
částic (hmotnosti excitací) mění. V uvedeném jednoduchém
případě by se při j =0, m2< 0 jednalo o teorii tachyonů
s imaginární hmotností m2(j=0) =
d2V/dj2|j=jo= - m2 < 0, zatímco po narušení
symetrie se čtverec hmotnosti excitací skalárního pole
stává kladný: m2(j=jo) = d2V/dj2|j=jo= 2.m2.
Základní myšlenka Higgsova-Kibbleova
mechanismu *) tedy
spočívá v tom, že do lagrangiánu kalibrační teorie se
zavede pomocné skalární pole (Higgsovo
pole) s
takovým interakčním potenciálem, aby došlo ke spontánnímu
narušení symetrie, přičemž však lagrangián jako celek by
zůstal kalibračně invariantní. Potom se kalibrační pole
budou efektivně chovat jako pole s nenulovou hmotností.
Kromě toho se v teorii objeví navíc tzv. Higgsovy
bosony -
skalární částice s nenulovou klidovou hmotností, jakožto kvanta těchto pomocných skalárních polí.
*) Tuto hypotézu poprve zavedli v r.1964
ve svých pracech autoři P.Higgs, F.Englert a R.Brout,
G.Guralnik, C.Hagen a T.Kibble. Higgsovo pole v r.1967 využili
S.Weiberg, A.Salam a S.Glashow při vybudování teorie elektroslabé
interakce s těžkými intermediálními bosony W±,Z° (je zmíněno
níže).
Ukazuje se tedy, že teorie všech
fundamentálních interakcí lze jednotně vytvářet v rámci
kalibračních teorií lišících se především kalibrační grupou. Kalibrační teorie tak tvoří
zároveň vhodnou základnu pro sjednocování
interakcí:
dva typy interakcí s kalibračními grupami G1 a G2 lze
sjednotit tak, že vytvoříme kalibrační teorii s kalibrační
grupou G, obsahující grupu G1´G2 jako svoji podgrupu. Při
konstrukci jednotných teorií slabých, silných a
elektromagnetických interakcí je tato základní idea doplněna
předpokladem, že před narušením symetrie všechny vektorové
bosony zprostředkovávající interakce byly nehmotné. Po
spontánním narušení symetrie (vlivem vzniku konstantních
skalárních polí v celém prostoru) však část vektorových
bosonů získá hmotnost a příslušné interakce se stanou
krátkodosahovými - symetrie mezi různými typy interakcí se
poruší.
Sjednocování elektromagnetických a
slabých interakcí
První výrazný
úspěch na této cestě byl zaznamenán při sjednocování
elektromagnetické interakce a slabé interakce v tzv. elektroslabou interakci - jedná se o Weinbergovu-Salamovu-Glashowovu
teorii. Před
vznikem konstantního skalárního Higgsova
pole H
má tato teorie kalibrační symetrii SU(2)´U(1)
a popisuje elektroslabé interakce částic způsobované
výměnami nehmotných vektorových bosonů. Po vzniku
skalárního pole H se symetrie spontánně naruší
až do podgrupy U(1), odpovídající část vektorových bosonů
(W+,W-,Z°) získá hmotnost (řádu ~
e.H » 102 GeV), příslušné interakce se
stanou krátkodosahovými ® slabé interakce, zatímco
další pole Ai zůstává nehmotné ® elektromagnetické pole. Podařilo se tak
sjednotit slabé a
elektromagnetické interakce do jedné teorie, v níž vystupují jako
dva různé aspekty téhož jevu.
Weinbergovu-Salamovu teorii elektroslabé
interakce lze dnes již považovat za experimentálně prakticky
ověřenou, protože v r.1973 byla v CERNu prokázána existence
tzv. slabých "neutrálních proudů" (způsobujících
reakce typu nm + e ® nm + e), a hlavně v r.1983 byly ve
vstřícnych proton-antiprotonovych svazcích (270 GeV proti 270
GeV) collideru velkeho protonoveho synchrotronu v CERN objeveny intermediální bosony W±,Z°, jejichž hmotnosti (mW
@ 82 GeV, mZ @ 93 GeV) i
způsoby rozpadu velmi dobře souhlasí s předpovědí
Weinbergova-Salamova modelu.
Elektro-slabá interakce s
intermediálními bosony W± velmi elegantně vysvětluje podstatu beta-radioaktivity pomocí transmutace
kvarků uvnitř neutronů či protonů - podrobněji je vyloženo v
§1.2 "Radioaktivita", část "Radioaktivita beta" monografie "Jaderná
fyzika a fyzika ionizujícího záření":
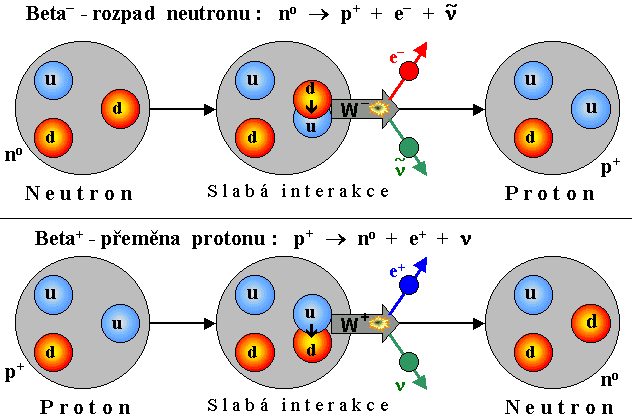
Schématické znázornění
mechanismu b--rozpadu neutronu (nahoře) a b+-přeměny
protonu (dole) v rámci standardního modelu elementárních
částic.
Silné interakce a kvarkový model
Než si
stručně povíme o další etapě sjednocování -
grandunifikačních teoriích, zmíníme se několika slovy o
specifických vlastnostech silných
interakcí (podrobnější výklad je v
§1.5 "Elementární částice", část "Kvarková
struktura hadronů" knihy "Jaderná
fyzika a fyzika ionizujícího záření"). Na základě obsáhlého
experimentálního materiálu, získaného převážně v 50. a
60. letech při hledání nových elementárních částic, byly
vypozorovány výrazné symetrie ve vlastnostech elementáních
částic, které v r.1964 vyústily zformulováním kvarkového modelu hadronů, podle něhož jsou všechny
hadrony složeny z ještě "elementárnějších"
částic - kvarků (tento
název byl s notnou davkou recese převzat z literárního díla
Jamese Joyce).
Kvarky jsou přitom fermiony se spinem 1/2 a třetinovým
elektrickým nábojem. Pro vysvětlení systematiky hadronů v
rámci aditivního kvarkového modelu bylo postupně zavedeno 6
druhů (v angličtině se požívá slovo flavour -
"vůně") kvarků označovaných "u" (up),
"d" (down), "s" (strange), "c"
(charm), "b" (bottom), "t" (top - na
existenci t-kvarku ukazuje nápadná symetrie v systematice leptonů a
kvarků). Z téhož důvodu bylo nutné přiřadit kvarkům nové
vnitřní kvantové číslo - "barvu" (color), která
nabývá tří diskrétních hodnot označovaných jako
"červená", "modrá", "žlutá";
přitom baryony jsou "bezbarvé" ("bílé")
kombinace tří barevnych kvarků, mezony pak
kombinace kvarků a antikvarků. Hlavní obtíž kvarkové
hypothézy však tkví v tom, že žádné volné částice s
vlastnostmi kvarků nebyly dosud nikdy pozorovány. Pokud tedy
kvarky vůbec existují, musejí být v hadronech velmi silně vázány.
Koncem 60.let byl kvarkový model do určité míry
podpořen výsledky experimentů s rozptylem vysokoenergetických
elektronů na nukleonech (hluboce nepružný rozptyl)
ukazujících na to, že při takovém "tvrdém
ostřelování" se nukleon nechová jako kompaktní
částice, ale jako shluk několika (tří) víceméně volných
rozptylových center - tzv. partonů. Přitom kvantová
čísla partonů (náboj, spin, izospin) odpovídala hodnotám
očekávaným u kvarků. Přímému ztotožnění kvarků a
partonů však bránil rozpor: na jedné straně se při
experimentech partony v nukleonech chovaly jako volné, na druhé
straně kvarky jsou tak silně vázány, že je nelze z nukleonů
uvolnit.
Kvantová
chromodynamika
Výrazného pokroku v chápání vlastností silné interakce
bylo dosaženo v 70.letech, kdy byla
zformulována a rozvinuta tzv. kvantová chromodynamika (QCD, řecky
chromos = barva)
[92],[55] jako teorie silné interakce; stejným právem se
může nazývat "kvarková
chromodynamika".
Tato teorie je vybudována podobným způsobem jako kvantová
elektrodynamika (QED), avšak je založena na neabelovských
kalibračních symetriích fyzikálně souvisejících s barvou
kvarků. Význačnou vlastností QCD je asymptotická
volnost:
efektivní vazbová konstanta vzájemného působení mezi kvarky
se blíží nule při zmenšování vzdáleností, ale prudce
roste se zvětšováním vzdálenosti. Asymptotická volnost
umožňuje přirozeně pochopit zdánlivě neslučitelné
vlastnosti kvarků jakožto partonů: kvarky na malých
vzdálenostech uvnitř nukleonů téměř neinteragují, zatímco
z hlediska větších vzdáleností jsou vázány velmi silně. S
asymptotickou volností tak těsně souvisí hypothéza dokonalého "uvěznění"
kvarků,
podle níž kvarky nemohou existovat jako volné částice
(nekonečně velká energie potřebná na uvolnění), ale pouze
vázané v hadronech.
Silná interakce mezi kvarky je v QCD
zprostředkována vektorovým kalibračním polem, jehož kvanta
s nulovou klidovou hmotností, zvaná gluony, zde hrají podobnou úlohu jako
fotony v QED. Na rozdíl od kvantové elektrodynamiky mají
gluony "barevný" náboj a interagují samy se sebou
(mohou se navzájem "emitovat"); v důsledku této
nelinearity má vakuum v QCD složitou strukturu, zvláště v
oblasti "infračervených" (nízkoenergetických)
vakuových fluktuací.
Jety - stopy po
hadronizovaných kvarcích
Za velmi vysokých energií při tvrdých a hluboce nepružných
srážkách elektronů s protony vzniká řada sekundárních
částic, které vylétají neizotropně v
jakýchsi směrovaných "výtryscích" - jetech.
Detailní analýza úhlového rozdělení a energie částic v
jetech ukázala následující mechanismus interakce, který lze
rozdělit do dvou etap: Během 1.etapy vysokoenergetický
elektron při interakci s protonem předá část své kinetické
energie jednomu z kvarků, který se po tomto rozptylu po
určitou kratičkou dobu pohybuje prakticky volně (asymptotická
volnost) uvnitř protonu; podobně i zbytek protonu tvořený
dvěma zbývajícími kvarky. Nedojde však k uvolnění kvarků
z protonu. Jakmile vzdálenost mezi vyzářeným kvarkem a
zbytkem protonu přesáhne zhruba 1fm (=10-15m), nastává 2.etapa: síly mezi nimi začnou prudce
narůstat a v kvark-gluonovém poli dojde k produkci kvarků a
antikvarků, které se zformují do mesonů a baryonů - dojde k
tzv. "hadronizaci" kvark-gluonového
plasmatu. Výsledkem je vyzáření dvou úhlově kolimovaných
spršek částic - jetů, které vylétají
přibližně ve směrech letu kvarku a zbytku protonu v první
etapě. Tyto jety jsou vlastně stopami po kvarcích.
Tento mechanismus je zjednodušeně
znázorněn na obrázku, který pochází z §1.5 "Elementární
částice" knihy "Jaderná
fyzika a fyzika ionizujícího záření":

V kvantové chromodynamice se vyskytuje
problém CP- narušení kombinace nábojové symetrie a parity v
teorii kvarků, který se řeší zavedením částic zvaných axiony
- jsou to lehké (klidová hmotnost cca 10-5eV) hypotetické částice se spinem 0, které se někdy
diskutují jako možná součást tzv. skryté (temné,
nezářící) hmoty ve vesmíru (viz §5.6
"Budoucnost vesmíru. Šipka
času. Skrytá hmota.").
Další podrobnosti o
vlastnostech elementárních částic a jejich interakcí jsou
uvedeny v §1.5 "Elementární částice" knihy "Jaderná fyzika a fyzika
ionizujícího záření".
Velké sjednocení
Máme-li k
dispozici teorii silných interakcí (QCD) a teorii
elektroslabých interakcí (Weinbergův-Salamův model), což
jsou všechno kalibrační teorie, vzniká přirozeně snaha
spojit tyto teorie do jedné ještě obecnější teorie
interakcí. Tato další etapa unitarizace se označuje jako velké sjednocení (GUT - Grand Unification
Theory).
Grupa
kalibrační symetrie G v tomto velkém sjednocení musí přitom
obsahovat podgrupy SU(3)color ´
[SU(2) ´ U(1)]elektroslab Ě G ; nejjednodušší grupou
tohoto druhu je SU(5), používají se však i modely s
kalibračními grupami SO(10), E6 a další [194].
V grandunifikačních teoriích se
vyskytují vektorové bosony X a Y (zvané též leptokvarky, protože způsobují přechody mezi
kvarky a leptony), které jsou před narušením symetrie -
stejně jako všechny ostatní vektorové částice - nehmotné;
leptony se přitom mohou snadno měnit na kvarky a naopak *).
První Higgsovské pole narušuje výchozí symetrii SU(5) na
SU(3) ´ SU(2) ´ U(1) - silné interakce popsané
grupou SU(3) se oddělují od elektroslabých popsaných grupou
SU(2) ´ U(1). X- a Y-mezony získávají velikou
hmotnost (řádově mX,Y ~1015GeV), čímž je přeměna
kvarků v leptony silně potlačena a proton se stává prakticky
stabilní. Další higgsovské pole pak narušuje symetrii mezi
slabými a elektromagnetickými interakcemi stejně jako ve
Weinbergově-Salamově modelu.
*) Tato okolnost mohla mít velký význam
při vzniku baryonové asymetrie ve velmi raných fázích
vývoje vesmíru (je diskutováno v §5.4 "Standardní
kosmologický model. Velký třesk. Formování struktury
vesmíru." a též v
§5.5).
Jednou z hlavních předpovědí
grandunifikačních teorií je nestabilita
protonu, který
by se měl rozpadat na miony či pozitrony a na jeden neutrální
či dva nabité piony [p ® (m+ nebo e+) + (po nebo p++p-)]
s dobou života řádově tp
» 1030-1033 roků. Tento rozpad by byl
způsoben přeměnou kvarku na lepton prostřednictvím bosonu X
a vzhledem k obrovské hmotnosti bosonu X je jeho
pravděpodobnost nesmírně malá. Pozorování rozpadu protonu
by však bylo velice důležité, protože by rozhodujícím
způsobem ukázalo, že grandunifikační teorie jde správnou
cestou. Experimenty *) zatím dávají odhady tp > 1030 let.
*) Tyto pokusy o pozorování rozpadu
protonu se provádějí hluboko pod zemí (z důvodu odstínění
kosmického záření), kde jsou umístěny velké nádrže s
vodou, opatřené mnoha fotonásobiči, které by mohly
zaregistrovat slabé záblesky způsobené průchodem rychlých
částic vzniklých jako produkty rozpadu protonu.
Nejdokonalejším zařízením tohoto druhu je Superkamioka-NDE
v Japonsku, které sice nezaznamenalo žádný rozpad protonu,
ale bylo velice úspěšné při detekci a spektrometrii neutrin
(viz část "Neutrina" v §1.2 knihy "Jaderná
fyzika a fyzika ionizujícího záření").
Myšlenka velkého sjednocení je jistě
velmi přitažlivá a slibná. Je zde však stále mnoho
potíží a nevyřešených problémů, např. problém
hierarchie hmotností generovaných mechanismem spontánního
narušení symetrie ve skalární části teorie, vystupuje zde
příliš mnoho volných parametrů (více než 20), není jasné
jak volit mezi několika alternativními modely a další;
GUT je příliš fenomenologická. Kromě toho grandunifikační
teorie nezahrnují gravitaci. Teorie pokoušející se o velké
sjednocení tedy zatím nejsou v takovém stavu, aby mohly být
považovány za "konečné" teorie interakcí. Nicméně
jejich použití např. v kosmologii již nyní vede k novým
zajímavým koncepcím prospěšným jak pro kosmologii, tak pro
fyziku elementárních částic - viz §5.5.
Supersjednocení a supergravitace
Názory na
úlohu gravitace ve struktuře elementárních
částic se velice různí; rozprostírají se mezi dvěma
krajními polohami:
Pokud lze univerzálnost gravitace
extrapolovat až do mikroměřítek elementárních
(subnukleárních) častic, platila by zcela určitě aspoň
první část druhého krajního názoru b). Lokální hustoty hmoty a
energie zde totiž dosahují takových hodnot, že gravitační
interakce by se stala silnou. Stále sílí názor, že v
současné době již nelze od sebe odtrhovat fyziku
elementárních částic a fyziku gravitace; zdá se dokonce, že
bez zahrnutí gravitace nemůže být vytvořena konzistentní a
jednotná teorie částic tvořících hmotu.
Je proto přirozená snaha završit
unitarizaci interakcí v kvantové teorii pole zahrnutím
gravitační interakce, jejím sjednocením s ostatními třemi
druhy interakcí. Tento ambiciózní unitarizační program se
označuje jako supersjednocení nebo
supergravitace.
Sjednotit gravitaci s ostatními druhy
interakcí v duchu výše zmíněného
schématu unitarizace
kalibračních teorií znamená sloučit vnitřní symetrie s
geometrickými, tj. najít společnou grupu zahrnující jak
grupu transformací prostoročasu (např. Poincaréovu grupu)
charakterizující gravitaci v OTR, tak i grupy vnitřních
(nikoliv prostoročasových) symetrií slabých, silných a
elektromagnetických interakcí. Ukázalo se, že provést
takové sjednocení (netriviálním způsobem, tj. ne jako pouhý
direktní součin) nelze v rámci Lieových grup, ale bylo nutné
použít nové algebraické struktury - zobecněné grupy nazývané
často Lieovy superalgebry nebo graduované Lieovy algebry.
Ve zobecněných grupách jsou příslušné algebry určeny jak
komutačními, tak i antikomutačními relacemi mezi
jednotlivými generátory. Ty Lieovy superalgebry, které obsahují jako
svoji podalgebru grupu prostoročasových transformací (např.
Poincaréovu grupu), se označují jako supersymetrické.
Algebra supersymetrie se konstruuje tak,
aby obsahovala vedle obyčejných generátorů Poincaréovy grupy
(prostoročasových posuvů Pk a rotací Mkj) také spinorové generátory Qi
s vhodnými komutačními relacemi. Pokud se taková algebra
realizuje v prostoru polí, transformují generátory Qi
tenzorová pole na spinorová a naopak. Protože v kvantové
teorii tenzorová pole popisují bosony s celočíselným spinem
(řídící se Bose-Einsteinovou statistikou) a spinorová pole
popisují fermiony s poločíselným spinem (statistika
Fermi-Diracova), operátory Qi vlastně generují transformace
převádějící fermiony na bosony a naopak. V supergravitaci je
tak odstraněna ostrá hranice kladená mezi fermiony a
bosony v dosavadní fyzice. Další charakteristickou vlastností
supergravitace je to, že vedle gravitačního pole, které je
kalibračním polem vůči lokálním transformacím
prostoročasu, obsahuje ještě spinorové pole - kalibrační
pole vzhledem k lokálním supersymetrickým transformacím
generovaným Qi; takové pole se označuje jako Raritovo-Schwingerovo a jeho kvantum
se nazývá gravitino (může mít spin 3/2, popř. 5/2 *).
*) V supersymetrických unitárních
teoriích elementárních částic je ke každé částici
přiřazen její tzv. superpartner - každý
boson má svého fermionového superpartnera a fermion má naopak
svůj bosonový protějšek. Nejčastěji diskutované
supersymetrické částice jsou zmíněná gravitina
a dále též fotina - slabě interagující hmotné
částice se spinem 1/2, zaváděné jako supersymetrický
partner fotonu. Někdy se diskutují i supersymetrické částice
k fermionům: s-leptony jako superpatneři k
leptonům, např. s-elektron, s-mion,
s-neutrino (zvané též neutralino
- mělo by mít vysokou hmotnost desítky GeV), či kvarkům -
skvark. O elementárních částicích je podrobněji
pojednáno v knize "Jaderná fyzika a fyzika
ionizujícího záření", §5.5
"Elementární částice".
Supersymetrie značí, že "silové" a
"látkové" částice (tj. pole a hmota) jsou dvě
stránky téže reality. Supersymetrie v principu umožňuje
vyřešit problém nekonečen tím způsobem, že příspěvky
uzavřených smyček ve Feynmanových diagramech pro virtuální
bosony vedou ke kladným nekonečnům a pro virtuální fermiony
k záporným nekonečnům, takže by se mohly v optimálním
případě vzájemně vyrušit.
Nejjednodušší supergravitační teorie
- tzv. prostá supergravitace vytvořená v r.1976 [89],[66],
byla spíše modelovým experimentem, protože obsahuje
minimální množství polí; nezahrnuje ani kvarky a leptony.
Fyzikálně realističtější varianty supergravitačních
teorií se snaží rozšířit počet spinorových generátorů a
zavést též generátory vnitřních symetrií. Vzniká tak rozšířená
supergravitace, která obsahuje 4N spinorových generátorů Qai (a =
1,2,...,N) nesoucích index vnitřní symetrie a. Omezíme-li se přitom na částice
(pole) se spinem nepřesahujícím hodnotu 2, v prostoročase
dimenze d=4 jsou možné N-rozšířené supergravitační teorie
s N = 1,2,...,8. Nejjednodušší rozšířenou supergravitační
teorií je N=2-supergravitace sjednocující Maxwellovu a
Einsteinovu teorii; k fotonům a gravitonům jsou zde přiřazena
dvě gravitina. Maximálně rozšířená N=8-supergravitace
obsahuje: jedno gravitační pole (graviton), 8 polí Raritových-Schwingerových
(gravitin), 28 vektorových polí (bosonů) se spinem 1, 56
spinorových polí (fermionů) se spinem 1/2 a 70 skalárních
polí. Multiplety rozšířených supergravitačních teorií
mají tedy mnohem bohatší strukturu než v prosté
supergravitaci. Avšak přesto, že obsahují nadměrný počet
polí, neobsahují pole některých známých částic, např. m-mezonu.
Z unitarizačního schématu na obr.B.8
vidíme dvě na první pohled diametrálně odlišné cesty:
Einsteinovu geometrickou cestu končící Wheelerovou
geometrodynamikou a cestu kvantových kalibračních teorií pole
vedoucí k supergravitaci, která nemá s geometrickým
charakterem nic společného. Protože Einsteinovo pojetí
gravitace jako geometrické struktury prostoročasu vychází z
velmi hlubokých a názorných principů, naskytá se přirozeně
otázka, zda geometrickými prostředky nelze konstruovat i
supergravitační teorie. Fyzikálně by to znamenalo, že
"náboje" v supergravitačních teoriích by měly mít
svůj původ v geometrické struktuře zobecněného
prostoročasu, podobně jako gravitační
"náboj" v OTR má původ v křivosti prostoročasu *).
*) Zajímavou variantou
vícedimenzionální unitární teorie, která se objevila v
poslední době, je teorie tzv. superstrun. V této teorii se částice a kvanta
polí interpretují jako vzbuzené stavy kmitů (jednorozměrné)
relativistické struny ve vícerozměrném prostoru
(nejčastěji d=10). Tyto superstruny s charakteristickou délkou
řádu Planckovy délky »10-33cm mohou být jak otevřené (s volnými
konci), tak uzavřené, přičemž interakce superstrun
spočívá buď ve spojení konců dvou strun (vznikne struna
třetí), nebo v roztržení jedné struny na dvě části. Za hlavní
výhodu teorie superstrun sa považují její lepší renormalizační vlastnosti -
nevyskytují se zde "ultrafialové" divegence. O teorii
superstrun je stručně pojednáno níže v samostatné pasáži
na konci této kapitoly.
Geometrická formulace
supergravitace. Vícedimenzionální unitární teorie.
Skutečně se ukázalo, že supergravitace může být
formulována jako geometrická teorie v superprostoru
(superprostor vzniklý rozšířením Minkowského prostoročasu
je obecně zakřivený a má navíc další rozměry spinorového
charakteru) s použitím aparátu diferenciální geometrie
zobecněného na situaci, kdy některé ze souřadnic
antikomutují. Jedná se tedy o prostor s torzí, přičemž se
ukázalo, že všechny komponenty křivosti mohou být
vyjádřeny pomocí torze a jejích
kovariantních derivací. Torze se tak stává důležitým
geometrickým objektem v supergravitaci.
Nejnovější
pokusy o geometrickou formulaci
supergravitace
tak vedou k určité "renezanci" Kaluzovy-Kleinovy
teorie (viz §B.2): konstruují se teorie v
mnoharozměrném
(d > 4) "prostoročase",
které by za pomoci spontánní kompaktifikace mohly dát
realistickou teorii
v prostoročase efektivní dimenze d=4.
Mechanismus spontánní kompaktifikace spočívá v tom, že se hledá
speciální vakuové řešení zobecněných Einsteinových
rovnic v d-rozměrném prostoročase, odpovídající
reprezentaci d-rozměrné variety ve tvaru ed = e4 ´ Bd-4, kde e4 je čtyřrozměrný prostoročas
(většinou se uvažuje Minkowského) a Bd-4 je kompaktní
"vnitřní" prostor. Nadbytečné d-4 dimenze ("extra-dimenze") jsou "svinuty" v dostatečně
malých měřítcích (uvažují se většinou Planckovská
měřítka 10-33cm), jak bylo diskutováno výše
v pasáži "Fyzikální
pole « fyzikální prostor ® sjednocení".
Celkový (výsledný) d-prostor ve
vícedimenzionálních unitárních teoriích pole je tvořen
vnějším 3+1 rozměrným
prostoročasem (obecně zakřiveným) a dalšími d-4 extradimenzemi (bývá jich 5-7) vnitřního prostoru.
Tyto extradimenze tvoří speciální varietu, jejíž geometrické
vlastnosti, především holonomie a konexe, vhodně modelují (unitární) symetrie
interakcí
elementárních částic - tím je sjednocují s geometrickou gravitací 3+1
rozměrného prostoročasu.
Základní idea vícerozměrných
unitárních teorií se zkompaktifikovanými dimenzemi spočívá
v tom, že fyzikální zákony, které pozorujeme, závisí na
geometrických vlastnostech dalších, skrytých extra-dimenzí. Ve vícedimenzionálních teoriích
existuje mnoho řešení, lišících se např. metrickou
velikostí kompaktifikací. Zkompaktifikované dimenze jsou
příliš malé, než abychom je mohli jakkoli pozorovat či
detekovat. Avšak různé geometrie dodatečných dimenzí
implikují různé druhy částic a sil, což v makroskopickém
světě vyvolává odlišné fyzikální jevy.
Byly studovány zobecněné
Kaluzovy-Kleinovy unitární teorie pro různé dimenze d > 4.
Aby taková teorie byla úplná a realistická, tj. aby
sjednocovala všechny známé interakce částic, musí obsahovat
fenomenologickou grupu vnitřní symetrie SU(3)´SU(2)´U(1). Jak nedávno ukázal Witten
[283], aby "vnitřní" prostor Bn měl SU(3)´SU(2)´U(1) - grupu izometrií, musí být jeho
minimální dimenze rovna n=7 tj. dimenze výchozí variety
Kaluzovy-Kleinovy teorie musí být d =
11, což se
shoduje s výsledkem pro maximální N=8-supergravitaci v
(d=4)-prostoročase, získaném v práci [59].
V kapitole 5 (§5.5
"Mikrofyzika a kosmologie. Inflační vesmír.")
byly diskutovány kosmologické důsledky grandunifikačních a
supergravitačních teorií. V nejranějších etapách vývoje
vesmíru při vysokých teplotách, kdy ještě nenastala
spontánní kompaktifikace, prostoročas mohl mít všech svých
11 rozměrů. Spontánní kompaktifikace, která potom nastala,
mohla vést v principu ke všem možným vakuovým řešením,
takže se mohly vytvořit "ostrovy", v nichž
prostoročas může mít různou topologii, počet rozměrů i
signaturu metriky. Nejranější vesmír by tak mohl být
jakýmsi "oknem" do vyšších dimenzí zobecněné
Kaluzovy-Kleinovy unitární teorie.
I když supergravitace dosud není
završena, jedná se nesporně o velmi nadějnou unitarizační
koncepci. Pro ověření správnosti cesty nastoupené
supergravitací by bylo podstatné, kdyby se podařilo
experimentálné prokázat existenci gravitin, která jsou pro
supergravitační teorie charakteristická. Zatím však
"labořatoří" pro nepřímé ověřování
supergravitačních teorií je pouze kosmologie - důsledky jevů
ve velmi raném vesmíru.
Teorie superstrun
Jedním z výchozích pojmů
fyziky je pojem hmotného bodu - idealizovaného
objektu, jehož hmotnost (i ostatní parametry) jsou
soustředěny do jediného geometrického bodu prostoru.
Trajektorie, kterou probíhá hmotný bod v prostoru je křivka,
jejíž každý bod lze charakterizovat prostorovými
souřadnicemi a časem. Dynamika hmotného bodu v klasické
mechanice je dána Newtonovými rovnicemi (§1.2), v
relativistické mechanice (§1.6) je popsána pohybem po
světočáře ve 4-rozměrném rovinném prostoročase STR, nebo
v zakřiveném prostoročase OTR (§2.4). V kvantové mechanice
je dynamika částice popsána Schrödingerovou rovnicí;
trajektorie, spojující počáteční a koncový stav částice
v prostoru, jsou východiskem i při kvantování pomocí
Feynmanových intergrálů přes trajektorie (§B5).
V klasické mechanice byl pojem hmotného bodu
pouhou idealizací skutečných těles,
výhodnou pro analýzu jejich pohybu. Speciální teorie
relativity však posílila důležitost pojmu hmotného bodu:
žádný elementární (fundamentální) objekt nemůže mít
konečné prostorové rozměry, neboť žádný signál či
interakce se nemůže šířit nadsvětelnou rychlostí. Při
srážce dvou těles nenulových rozměrů nemohou všechny
části reagovat ihned, z čehož plyne, že těleso je složeno
z elementárnějších objektů: Ţ elementární objekt musí být bodový.
Bodový charakter fundamentálních objektů -
zdrojů pole - však vede k závažným problémům v teorii
pole: při limitních přechodech k nulovým rozměrům vznikají
matematicky divergující výrazy vedoucí k nekonečným
hodnotám. Těchto divergencí je třeba se zbavit (v
podstatě ad hoc) metodami renormalizace
- provést třebas vhodnou kalibrační transformaci tak, aby se
výsledky výpočtu shodovaly s experimentálními hodnotami.
Podařilo se však najít způsob, jak se těmto
nepříznivým matematickým divergencím vyhnout systematicky -
jsou to teorie, v nichž namísto bodů jsou elementárními
objekty jednorozměrné čáry či smyčky
nenulové délky - tzv. struny. Pokud by tyto
struny byly dostatečně malé (mikroskopické), nemusejí být
pozorovatelné - vypadaly by "z dálky" jako body.
Základními stavebními "kameny" přírody by tedy
nebyly částice s nulovými rozměry, ale jednorozměrné
struny, které vibrují různými způsoby,
odpovídajícími různým různým druhům částic. A interakce
částic by odpovídaly spojování a rozpojování strun. Struny
jsou v zásadě stejné, ale odlišují se mírou (modem) svých
vibrací - podle toho může být struna, zjednodušeně
řečeno, např. elektronem nebo kvarkem.
Podle této koncepce všechno co je ve vesmíru
- všechny síly a veškerá hmota - jsou vytvořeny z malých
vibrujících energetických linií zvaných superstruny. Různé
způsoby, kterými struna rezonančně vibruje, představují
různé druhy částic. Různé druhy sil a částic mohou
pocházet z různých vibrací téže struny. Jedním z hlavních
úskalí teorie superstrun je otázka jejich experimentálního
ověření. Superstruny, pokud existují, jsou nesmírně malé
(Planckovských rozměrů). Není proto naděje na jejich
přímé experimentální prokázání...
Popis pohybu volné
struny
Volná (relativistická) částice o klidové hmotnosti mo v prostoročase (d=4)
se popisuje integrálem akce (viz §1.6) S0 = mo. ň ds = mo.ňÖ[(dxi/dt)(dxi/dt)] dt , kde s je
prostoročasový interval a t vlastní čas částice. Tato akce S0 (index
"0"
zde vyjadřuje, že se jedná o bodovou, tj. 0-rozměrnou
částici) je úměrná délce
světočáry částice (relativistickému intervalu s)
- obr.B.10 vlevo. Variační princip nejmenší akce dS = 0 pak vede k
Lagrangeovým rovnicím, z nichž plynou pohybové rovnice
relativistické mechaniky ve STR (1.100), resp. (2.5b) v OTR.
Tento postup lze zobecnit i na jiný počet dimenzí než d=4.

Obr.B.10.
Vlevo: Trajektorie "0-rozměrné"
volné částice v prostoročase je 1-rozměrná světočára,
kterou lze parametrizovat délkou intervalu s nebo
vlastním časem t.
Vpravo: Trajektorií, kterou 1-rozměrná struna
proběhne v prostoročase, je 2-rozměrná světoplocha, kterou
lze parametrizovat vlastním časem t a dalším parametrem s,
charakterizujícím polohu bodu na křivce znázorňující
strunu.
Přirozené zobecnění integrálu akce z
hmotného bodu na strunu vede k tomu, že akce struny bude
úměrná velikosti světoplochy, kterou struna
"zamete" při svém pohybu (evoluci) v prostoročase -
obr.B.10 vpravo: S1 = T. ň Ö[det(hab)] ds dt , kde hab (a,b = 1,2) je dvourozměrná metrika na světoploše; T
popisuje "napětí" struny,
dané hmotností struny na jednotku délky.
..................
.....doplnit....... relativistický a
kvantový popis struny .......
......
Teorie strun v silné
interakci
Teorie strun má spletitou historii. Představa jednorozměrných
objektů - strun - se zrodila na konci 60.let
při jednom z pokusů o popis silných interakcí. Studium
srážek hadronů (především p-mezonů) při vysokých
energiích vedlo k tzv. Venezianově modelu, který
amplitudy účinných průřezů kvantifikuje pomocí součinů a
podílů G-funkcí, jejichž argumentem jsou druhé mocniny
součtů 4-hybností interagujících částic a částic
výsledných. Ukázalo se, že spektrum Venezianova modelu je
identické se spektrem normálních modů "vibrace"
jednorozměrného kvantovaného objektu - relativistické
struny (v r.1968 si toho všimli
M.Virasoro a J.Shapiro). A Feynmanovy
diagramy, popisující interakce dvou částic, lze sjednotit do
jednoho diagramu, v němž 4 interagující částice (2
vstupující a 2 vystupující) jsou znázorněny jako otevřené
struny (lineární útvary
topologicky ekvivalentní úsečce);
stejně tak lze znázornit i výměnné částice
zprostředkující interakci. Každá struna přitom může
"vibrovat" různým způsobem a podle toho se jevit
jako částice určitého druhu (elektron, foton, ...) -
částice jsou vzbuzenými stavy
"vibrace" struny. Přesněji řečeno, různé vibrace
struny modelují různé základní částice.
Pozn: Velikost
superstrun se zde uvažovala v řádu 10-13cm, odpovídající charakteristickému dosahu silné
interakce.
Podrobná matematická
analýza ukázala, že kvantová teorie bosonové struny je
konzistentní (např. ve smyslu konformní invariance) jen tehdy,
je-li dimenze prostoročasu d=26. To dramaticky převyšuje
pozorovaný počet dimenzí d=4 našeho prostoročasu. Tento
nesoulad je možné vyřešit hypotézou o "svinutí"
neboli kompaktifikaci přebytečných dimenzí
do malých uzavřených (kompaktních) variet, jak to bylo
zmíněno výše v souvislosti se zobecněnými
Kaluzovými-Kleinovými unitárními teoriemi, nebo v §5.7 v
souvislosti s kvantovou kosmologií velmi raného vesmíru.
Dalším nedostatkem původní teorie strun je, že ve
spektru volné bosonové struny (které obsahuje pouze
transverzální mody) základní stav odpovídá částici se
záporným kvadrátem hmotnosti, tj. částici s imaginární
hmotností - tachyonu (možnost existence
tachyonů jsme z principiálních důvodů, především z
hlediska kauzality, vyloučili již v §1.6). Druhý excitovaný
stav je již příznivější - odpovídá kvantu s nulovou
klidovou hmotností a se spinem 2, které lze ztotožnit s
gravitonem, viz níže.
V polovivě 70.let byla
vytvořena kvantová chromodynamika (byla
stručně zmíněná výše), která silné interakce
interpretuje pomocí kvarků a gluonů, které na sebe působí
prostřednictvím tzv. "barevného náboje". Velký
úspěch kvantové chromodynamiky odsunul dosavadní strunové
modely na více než 10 let do pozadí.
Pozn.: Někteří
fyzikové si ale v té době představovali, že kvarky v
hadronech jsou spojeny strunami (gluonovými trubicemi), které
je drží pohromadě jako "gumová vlákna" (H.B.Nielsen, Y.Nambu, L.Suskind).
Supersymetrická
teorie strun
Jak bylo výše v pasáži o supergravitaci nastíněno,
pokusy o sjednocení gravitační interakce s ostatními typy
interakcí v rámci kalibračních kvantových teorií pole vedly
k pojmu supersymetrie. Tato teorie spojuje
bosony a fermiony: ke každému bosonu předpovídá
"superpartnera" kterým je fermion, a naopak. Aplikace
těchto nových symetrií, vyjádřených geometricky
(komutačními i antikomutačními relacemi v prostoročase) na
teorii strun vedla ke snížení potřebného počtu rozměrů
prostoročasu z původních d=26 na d=10 (a
neobsahovala již žádný tachyon). Vznikla tak supersymetrická
teorie strun, neboli teorie superstrun.
Vedle bosonové struny zde jako její partner vystupuje
fermionová struna, neboli superstruna, která má další,
spinorovou proměnnou.
Ve spektru excitací
relativistické kvantované struny se vyskytuje částice s
nulovou klidovou hmotností a spinem s=2, kterou lze
identifikovat s gravitonem - kvantem
gravitačních vln. To přivedlo J.Sherka a J.Schwarze v r.1974 k
myšlence, že i když teorie strun není vhodná pro popis
silných interakcí, mohla by se stát vhodným nástrojem k
budování kvantové teorie gravitace. Přitom
však velikost těchto hypotetických strun je nutno z původně
uvažovaných 10-13cm radikálně zmenšit na rozměry 10-33cm Planckovy-Wheelerovy
délky, charakteristické pro kvantovou gravitaci
(zavedené v §B.4).
Struny, či superstruny,
jsou elementární jednorozměrné útvary, jež mohou - jakožto
rezonátory - vibrovat v různých frekvenčních módech.
Vibrace, jež jsou určeny rozměry struny a jejím napětím,
jsou kvantovány, příslušná energie nabývá diskrétních
hodnot. Frekvence těchto vibrací a počet vln určují
základní vlastnosti částic (např. hmotnost či náboj).
Jelikož má struna malé rozměry, může kmitat i v dalších
nezávislých "směrech", daných extra-dimenzemi.
Excitace superstrun mohou být "vibrační",
"rotační", i excitace "vnitřních stupňů
volnosti" - vnitřní symetrie, supersymetrie. Různé
kvantové excitace (normální mody superstruny) se interpretují
jako spektrum elementárních částic. Toto spektrum se ukazuje
být natolik bohaté, že může modelovat nejen všechny
stavební prvky standardního modelu elementárních částic,
ale zahrnovat i kvantovou gravitaci. Úspěšné dokončení
koncepce superstrun by tak představovalo jednotný
přístup k různorodému světu elementárních
částic a všech jejich interakcí - mohlo by být dosaženo
tzv. "teorie všeho" TOE (Theory Of Everything).
Skutečně dokonalá unitární teorie "všeho" by měla vysvětlit i původ a konkrétní hodnoty základních přírodních konstant, resp. poměry těchto konstant. Toto otázka je z kosmologického hlediska stručně diskutovaná v §5.5, pasáž "Původ přírodních konstant".
-------- níže uvedené poznatky vznikly až po sepsání knihy "Gravitace, černé díry ...", takže v knižním vydání nebyly obsaženy -----
Další dimenze, M-teorie, 11-rozměrná
teorie superstrun
Další vývoj teorie superstrun pokračoval výzkumy M.Grena,
J.Schwarze a E.Wittena, kteří nalezli takové kalibrační
grupy, aby teorie superstrun byla plně kovariantní v
prostoročase (v duchu OTR). Bylo nalezeno pět takových modelů
teorie superstrun, z nichž nejzajímavější se jevily dvě
tzv. heterotonické teorie s kalibračními grupami
SO(32) a S8´S8.
Významnou úlohu v teorii superstrun v posledních letech
sehrála analýza matematické (a z toho následně plynoucí i
fyzikální) ekvivalence neboli duality mezi
různými modely superstrun. Tyto duality představují nové
typy symetrií, sjednocující různé modely, které mohou mít
na první pohled odlišnou formu, avšak vedou k rovnocenným
fyzikálním výsledkům. Byly nalezeny dva typy dualit mezi
stávajícími modely superstrun. S-dualita se
projevuje ekvivalencí dvou modelů superstrun, v nichž
zaměníme vazbovou konstantu g za její převrácenou
hodnotu: g ® 1/g. T-dualita má geometrický
charakter: model s určitou souřadnicí, zkompaktifikovanou na
kružnici poloměru R, je ekvivalentní jinému superstrunovému
modelu s kompaktifikací na kružnici ~ 1/R (přesněji Lstr2/R, kde Lstr je délka superstruny). Někdy je diskutována i tzv. U-dualita,
vzniklá kombinací S a T-duality.
Dalším důsledkem dualit a
sjednocení superstrunných modelů je rozšíření vlastní
dimenze strun z původní d=1 na objekty s jiným (vyšším)
počtem p prostorových rozměrů, např. 2-rozměrné
objekty - membrány (odtud je odvozen zkrácený
název "brány"). Takovéto vícerozměrné
objekty se již nenazývají superstruny, ale p-brány:
pro p=0 se jedná o bod, pro p=1 je to struna, pro p=2 membrána,
atd.
Studium strunových dualit
ukázalo, že všechny stávající teorie superstrun lze sloučit
do obecnější teorie, zvané M-teorie (E.Witten, 1995; označení "M" pochází z
názvu membrane, někteří autoři jej dávají do
souvislosti s přívlastky mystery, magic a
pod.) *). Takovou sjednocenou M-teorii lze
přitom realizovat pomocí zvýšení dimenze
variety na d=11. Srovnáme-li to s koncepcemi
výše uvedené supergravitace, vidíme, že počet dimenzí se
shoduje s 11-rozměrnou supergravitací; těsné
souvislosti mezi oběma unitárními teoriemi, aspoň v
nízkoenergetickém limitním případě, byly byly též
analyticky prokázány.
*) Byla též navržena další varianta,
tzv. F-teorie (C.Vafa,
1996), používající primárně 12
rozměrů, z nichž však dva jsou imanentně stočeny (do 2-toroidu). Poskytuje velké
množství řešení, potenciálně snad použitelných v
modelech částicové fyziky...
Alegoricky se někdy označení
"M" dává do souvislosti s "Matkou" a
"F" s otcem "Father".
Šest extra-dimenzí
obecného prostoru je zkompaktifikováno do vnitřní tzv. Calabi-Yau
variety, jejíž geometrické vlastnosti SU(n) holonomie
vhodně modelují symetrie interakcí a
elementárních částic. Elementární superstruny mohou kmitat
do různých dimenzí. Geometrická struktura vnitřního
prostoru určuje zákony jednotlivých interakcí mezi
elementárními částicemi a hodnoty fyzikálních konstant
(jako jsou náboje a hmotnosti částic), které jednotlivé
částice charakterizují - tedy "zjevné" přírodní
zákony ve "vnějším" 3-rozměrném prostoru. Tyto
základní fyzikální zákony, které jsme v naší přírodě a
vesmíru vypozorovali, jsou zde však důsledkem vnitřních
fundamentálnějších zákonů unitární teorie superstrun *).
*) Tyto unitární teorie připouštějí mnoho řešení
s použitím různých akcí (lagrangiánů) a též v
závislosti na tom, jak je vnitřní prostor zkompaktifikován.
Těchto řešení může být nepřeberné množství. Můžeme
to interpretovat i jako různé vesmíry s
různými zjevnými zákony v 3+1-rozměrném prostoročase, což
nás opět přivádí k úvahám o "multiverzu"
v §5.5 "Mikrofyzika a kosmologie. Inflační vesmír" a v §5.7 "Antropický princip a existence více
vesmírů"...
Stručně shrnuto :
Všechno ve vesmíru je vytvořeno z malých vibrujících strun,
které mohou kmitat různými způsoby a do různých směrů -
dimenzí. Dodatečné "extra-dimenze" jsou nesmírně
malé, takže je nemůžeme pozorovat ani změřit. Jsou
stočené do malých smyček v Calabi-Yau varietě a ovlivňují
pouze jevy v nejmenších sub-sub-mikroskopických měřítcích.
Žijeme na 3(+1) - dimenzionálním řezu vícedimenzionálního
prostoru; takový řez se nazývá brána.
Všechny známé částice a síly jsou lokalizované na této
bráně. Snad kromě gravitace, která podle některých hypotéz
může "prosakovat" do dalších dimenzí (tím se někdy odůvodňuje, proč je tak slabá)..?..
Astrofyzikální a kosmologické
důsledky teorií superstrun
Podobně jako u dřívějších kvantových teorií pole a
vícedimenzionálních unitárních teorií, i zde se nabízejí
zajímavé hypotézy astrofyzikálních a kosmologických
důsledků *) teorie superstrun.
*) Diskuse některých kosmologických
důsledků kvantových a vícedimenzionálních teorií byla
nastíněna již např. v §5.5 "Mikrofyzika a
kosmologie. Inflační vesmír" a
v §5.7 "Antropický princip a existence více vesmírů". Astrofyzikální důsledky pro fyziku černých
děr pak v §4.7 "Kvantové vyzařování a
termodynamika černých děr".
Různá řešení teorie superstrun, jakož
i dalších unitárních teorií pole, mohou předpovídat různé
vesmíry s různými vlastnostmi (dimenzemi, hodnotami
fyzikálních konstant či spektry hmotností elementárních
částic); k reflexi těchto možností a jejich selekci možná
řekne své i antropický princip - viz "Antropický
princip aneb kosmický Bůh".
Rozhodnout mezi různými
verzemi vzniku vesmíru na základě astronomických pozorování
je velmi obtížné. Jedinou možností testování
počátečních fází vesmíru je detekce reliktních
gravitačních vln (zmíněných v §5.5), které jako
jediný druh záření mohly projít hustou a ionizovanou látkou
zaplňující raný vesmír. Tyto prvotní (reliktní)
gravitační vlny by měly odlišné spektrum pro
různé scénáře iniciálních fází vývoje vesmíru (např. pro inflační model by amplituda vln rostla
směrem k dlouhým vlnovým délkám, pro ekpyrotický model
naopak ke krátkým vlnovým délkám).
Jejich změření však bude možné až v budoucnu pomocí
velkých detektorů umístěných ve vesmíru, jako je
připravovaná LISA (§2.7, část "Detekce gravitačních vln", závěrečná pasáž).
Další možností je podrobná analýza fluktuací a polarizací
reliktního mikrovlnného záření, které by mohlo být
"modulováno" primordiálními gravitačními vlnami.
Závěrečná poznámka :
Teorie superstrun je v současné době ve stádiu intenzívního
rozvoje. Kromě průkopníků J.Schwarze, M.Greena,
E.Wittena, .......... na ní pracuje několik stovek fyziků
(především mladší generace) a řada výzkumných skupin. Z
našich fyziků se teorii superstrun velmi aktivně a úspěšně
věnují zejména P.Hořava a L.Motl, ...[..],[..]....
Superstrunová teorie je mnohými fyziky považována za
nejnadějnějšího současného kandidáta na úplnou
unitární teorii pole, sjednocující všechny 4 typy
interakcí a též kvantovou fyziku s obecnou teorií relativity,
na toužebně očekávanou "teorii všeho".
Řada fyziků je však k teorii superstrun skeptická.
Poukazují na nejednoznačnost jejích závěrů, neprůhlednost
a přílišnou matematickou komplikovanost, především pak na
obtížnost, ba nemožnost experimentálního ověření
v dohledné budoucnosti.
Určité možnosti nepřímého ověření by
mohly vyplývat z experimentálního měření elektrického a
gravitačního silového působení na mikroskopicky krátkých
vzdálenostech, kde by obvyklý zákon obrácených čtverců ~1/r2 mohl být jemně
modifikován závislostí ~1/r2+d, v níž by se projevoval počet dodatečných
(skrytých) dimenzí d..?.. A obecně měření
částicových interakcí na urychlovačích při čím dál
vyšších energiích, v nichž by se mohly projevovat napatrné
anomálie od standardního modelu...
| Gravitace, černé díry a fyzika prostoročasu : | ||
| Gravitace ve fyzice | Obecná teorie relativity | Geometrie a topologie |
| Černé díry | Relativistická kosmologie | Unitární teorie pole |
| Antropický princip aneb kosmický Bůh | ||
| Jaderná fyzika a fyzika ionizujícího záření | ||
| AstroNuklFyzika ® Jaderná fyzika - Astrofyzika - Kosmologie - Filosofie | ||