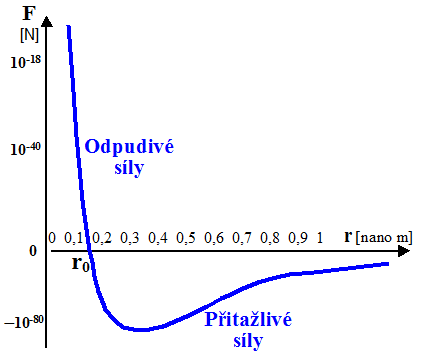
 |
Typická
závislost sil F, působících mezi atomy nebo
molekulami v látkách, na vzdálenosti r. |
1{font-size:18px;}
| AstroNuklFyzika ® Jaderná fyzika - Astrofyzika - Kosmologie - Filosofie | Fyzika a nukleární medicína |
1.
Jaderná a radiační fyzika
1.0. Fyzika - fundamentální
přírodní věda
1.1. Atomy a atomová jádra
1.2. Radioaktivita
1.3. Jaderné reakce
1.4. Radionuklidy
1.5. Elementární
částice
1.6. Ionizující
záření
1.1. Atomy a atomová jádra
Látka, pole,
částice, interakce
Úvodem našeho pojednání o atomech, atomových jádrech a
fyzice mikrosvěta si učiníme pár předběžných poznámek o
základních stavebních "kamenech" hmoty a o povaze
sil, které řídí jejich chování. Všechny tyto zde jen
nastíněné poznatky budou v průběhu výkladu na patřičných
místech vždy podstatně rozšiřovány a precizovány.
Při fyzikálním zkoumání přírody si
veškerý materiální svět rozdělujeme na dvě základní
formy hmoty :
Moderní fyzika ukazuje, že toto rozdělení je do určité míry konvenční - obě formy se vzájemně proměňují; částice látky mohou být interpretovány jako kvantové stavy specifických polí (unitární teorie pole a částic) a fyzikální pole lze popisovat pomocí kvant - částic (viz níže "Kvantová teorie pole").
Diskrétní
částicový a kontinuální polní model hmoty
Stavbu a chování hmoty ve fyzice modelujeme výše zmíněnými
dvěma odlišnými způsoby (formami matérie):
¨
Model
diskrétních částic, podle
něhož se všechna tělesa a hmotná prostředí skládají z
velkého množství drobných prostorově lokalizovaných
objektů - částic. Podle klasických
představ částice mají určitou nenulovou hmotnost či
energii, mají určitou polohu v prostoru a čase, určitou
rychlost, hybnost a kinetickou energii. Pohyb částic se řídí
univerzálními zákony mechaniky
(idealizovaného "hmotného bodu") - klasické
mechaniky (Newtonovy pohybové zákony) či relativistické
kinematiky a dynamiky. Nyní víme, že pro detailní analýzu
částic v mikrosvětě nevystačíme s klasickou mechanikou,
nýbrž musíme použít její zobecnění - kvantovou
mechaniku.
¨
Model
spojitého pole, popisující
strukturu a chování hmoty veličinami spojitě
rozprostřenými v prostoru. V moderní fyzice se tento
polní popis používá pro silová působení - interakce
- mezi částicemi látky. Je dokonale propracován zvláště
pro elektromagnetické jevy mezi nabitými tělesy a
částicemi - Faradayova-Maxwellova elektrodynamika (viz níže "Elektromagnetické pole a záření"). I zde pro detailní
analýzu jevů v mikrosvětě musí být použita kvantová
teorie pole, nejen elektromagnetického, ale i pole
silných a slabých interakcí (viz
níže "Kvantová teorie pole",
"Silné
jaderné interakce" a
"Radioaktivita beta. Slabé interakce").
Polní popis se však dá
použít (a zvláště dříve se často používal) i ve fyzice
kontinua pro studium kapalin, plynů a částečně i
pevných látek. Pohyb kapalin a plynů je vnitřně způsoben
pohyby jejich atomů a molekul - dokonale ověřená kinetická
teorie. Pro makroskopický popis chování plynů a
kapalin se však nevyšetřuje pohyb jednotlivých atomů či
molekul, ale kolektivní pohyby souboru
částic. Používají se "zprůměrované" veličiny,
které jsou spojitě rozloženy v celém objemu plynu či
kapaliny. Individuální údaje o poloze jednotlivých atomů
jsou nahrazeny průměrným prostorovým rozložením jejich
počtu - rozložením hustoty. Rychlost
neuspořádaného pohybu jednotlivých atomů je při
makroskopickém popisu nahrazena teplotou,
uspořádaného pohybu pak průtokem (přenosem
hybnosti) v různých místech látkového prostředí. Srážky
a silové působení mezi atomy či molekulami uvnitř plynů a
kapalin je vyjádřeno rozložením tlaku. Pro
vzájemné závislosti mezi těmito veličinami platí
důležité stavové rovnice. Vztah mezi
mechanickými charakteristikami částic (atomů a molekul) a
polními stavovými veličinami se ve fyzice kontinua odvozuje
metodami statistické fyziky. Veškeré
vlastnosti látkových prostředí a děje v nich pozorované
jsou integrálním projevem řady chaotických
či koordinovaných jednodušších pohybů stavebních částic
příslušné látky.
Základní
stavební částice hmoty
Při čím dál hlubším pronikání do mikrosvěta stavby hmoty
fyzika zjišťuje, že atomy (považované dříve za
nedělitelné), jsou složeny z částic, které
již dále nelze rozložit na jednodušší objekty schopné
samostatné existence. Tyto nejmenší již dále nedělitelné
částečky se označují jako elementární částice
a můžeme je považovat za základní "stavební
kameny" hmoty. Tyto elementární částice však nejsou
statické a neměnné, nýbrž mohou procházet vzájemnými proměnami
a některé z nich mohou vykazovat určitou vnitřní
strukturu. Při studiu stavby atomů se setkáváme
především se třemi nejdůležitějšími částicemi - elektronem,
protonem a neutronem *). Při
studiu excitací a záření atomů a atomových jader pak
ještě s fotonem - kvantem elektromagnetického
záření, při radioaktivitě dále s neutrinem
a pozitronem (antičásticí k elektronu) - §1.2, část "Radioaktivita
beta".
Vlastnosti těchto a řady dalších částic jsou podrobněji
rozebírány v §1.5 "Elementární
částice a urychlovače"
věnovanému fyzice elementárních částic,
kde je podána i systematika elementárních
částic (o neutrinech je kromě toho
podrobně pojednáno v §1.2, část "Neutrina - "duchové"
mezi částicemi").
*) Důvod, proč je pozorovaná hmota
složena z elektronů, protonů a neutronů spočívá v tom, že
všechny ostatní hmotné částice jsou velmi nestabilní.
Čtyři
základní fyzikální interakce
Vzájemné působení mezi částicemi látky lze vysvětlit
čtyřmi základními fyzikálními interakcemi.
Na úrovni atomových jader a elementárních částic se
dominantně projevují dvě interakce krátkého dosahu:
¨
Silná
interakce, důležitá zejména
tím, že udržuje pohromadě atomová jádra (viz níže "Atomové jádro"). Primárně slučuje kvarky do protonů a neutronů,
mesonů a dalších hadronů. Vlastní silná interakce
mezi kvarky, zprostředkovaná gluony, má dlouhý dosah, avšak
jaderná silná interakce, jakožto její "zbytkový
projev", je krátkodosahová (viz níže "Silná interakce").
¨
Slabá
interakce, která se uplatňuje
při vzájemných přeměnách neutronů a protonů za účasti
neutrin, v praxi hlavně při radioaktivitě b (§1.2, část "Radioaktivita
beta", pasáž "Mechanismus
slabých interakcí"). Je rovněž krátkodosahová.
¨
Určité druhy částic, které nazýváme elektricky
nabité, vykazují vzájemné silové působení
popsané interakcí
elektromagnetickou. Jsou-li tyto
elektricky nabité částice v klidu, působí mezi nimi
přitažlivá nebo odpudivá elektrická síla
podle Coulombova zákona, jsou-li v pohybu, přistupuje ještě
síla magnetická, při nerovnoměrných
pohybech nábojů pak i vyzařování elektromagnetických vln -
fotonového záření (viz níže pasáž
"Elektromagnetické pole a záření"). Elektromagnetická
interakce má dlouhý dosah (přesněji řečeno, dosah je nekonečný).
¨
Čtvrtá interakce, rovněž dlouhého
dosahu, je gravitační
interakce, která působí univerzálně
mezi všemi částicemi, je přitažlivá a
výrazně se projevuje u těles velké hmotnosti. Její silové
projevy jsou v klasické fyzice popsány Newtonovým
gravitačním zákonem, v relativistické fyzice Einsteinovými
rovnicemi gravitačního pole - viz knihu "Gravitace, černé díry a fyzika prostoročasu", §1.2 "Newtonův gravitační zákon" a §2.5 "Einsteinovy rovnice
gravitačního pole".
Největším a
nejobtížnějším úkolem současné teoretické fyziky je
nalezení tzv. unitární teorie pole, která by
4 základní interakce sjednotila a vysvětlila
by je jako zvláštní případy jediné všeobecné interakce -
viz pasáž "Unitární teorie pole a elementárních částic" v §1.5, podrobněji pak kapitolu "Unitární
teorie pole a kvantová gravitace"
shora zmíněné monografie "Gravitace, černé díry a
fyzika prostoročasu".
Velikosti silových účinků těchto základních
interakcí se diametrálně liší a
rozhodujícím způsobem závisejí na vzdálenosti
interagujících částic. Pro vzdálenosti řádu 10-13cm, odpovídající
rozměrům atomových jader, je relativní poměr (či lépe řečeno "nepoměr"!) silového působení silné, elektromagnetické, slabé
a gravitační interakce přibližně 1 : 10-(2-3) : 10-15 : 10-40. Při
vzdálenostech řádu 10-8cm, odpovídající rozměrům atomového obalu, se
krátkodosahové silné a slabé interakce již prakticky
neuplatňují a rozhodující vliv má interakce
elektromagnetická.
Gravitační interakcí, která se výrazněji
uplatňuje u makroskopických těles a dominantní charakter
získává až u těles kosmických rozměrů a hmotností, se v
našem pojednání o jaderné a radiační fyzice zabývat
nebudeme. Silnou a slabou interakci budeme podrobněji rozebírat
níže v příslušných pasážích o atomovém jádře ("Atomové jádro") a v §1.5 o elementárních částicích (část "Čtyři
typy interakcí"). O
elektromagnetické interakci si pár základních informací
řekneme zde (níže "Elektromagnetické
pole a záření"), neboť ji při výkladu budeme potřebovat nejdříve
- již v nauce o atomech.
Klasické
a kvantové modely v mikrosvětě
V atomové a jaderné fyzice zkoumáme objekty a děje, jejichž
chování se vymyká naší představivosti založené na
zkušenostech z makroskopického světa - z chování předmětů
složeného z velkého souboru atomů. I v mikrosvětě,
ovládaném kvantovými zákonitostmi (viz
níže) si občas můžeme vypomoci názornými mechanickými
přirovnáními k nám známým systémům
makroskopickým. Třebas elektrony v atomech si představujeme
jako lehké záporně nabité "kuličky" obíhající
kolem těžké kladně nabité "kuličky" - jádra
atomu. Nebo jindy si částice představujeme jako vlny či
vlnová klubka. Musíme však neustále mít na paměti, že se
jedná jen o modely, vyjadřující jen
některé vybrané vlastnosti těchto mikrosystémů, nikoli
jejich skutečnou materiální strukturu v běžném smyslu! Jsou
to všechno jen naše lidské modely, jak aspoň rámcově
pochopit jevy, které jsou naší denní zkušenosti velmi cizí.
Důležité je, že to funguje ve vztahu
teorie-experiment; a věříme, že nám to pomůže i k
pochopení vnitřních mechanismů..?..
Důležitým rozdílem oproti klasické fyzice je stochastický
(pravděpodobnostní) charakter kvantových jevů v mikrosvětě.
Pro jednotlivé procesy nedovedeme stanovit kdy přesně
nastanou, ale pouze jejich pravděpodobnost.
Individuální kauzalita chování částic se ztrácí, ale
objevuje se nový druh stochastické zákonitosti.
Chaotická náhodnost (zdánlivá či
principiální?) v chování individuálních částic vyúsťuje
v zákonitost pro statistický soubor těchto
částic jako celek (nikoli pro jeho jednotlivé prvky). Tyto
aspekty kvantové fyziky budou stručně diskutovány níže ("Kvantová povaha mikrosvěta").
Vztahy makrosvěta, mikrosvěta a megasvěta jsou z
filosoficko-přírodovědného hlediska rozebírány v §1.0
"Fyzika - fundamentální přírodní
věda".
Vakuum - prázdnota - nicota ?
Ve fundamentální fyzice se jevy, probíhající s tělesy,
částicemi a poli, zkoumají většinou ve vakuu. Vakuum
v klasické fyzice znamená prázdný prostor (lat. vacuus = prázdný),
přibližně dosahovaný v pozemských podmínkách v
uzavřených nádobách vyčerpáním vzduchu tak, aby tlak plynu
byl podstatně nižší než při normálním atmosférickém
tlaku. Ideální či dokonalé vakuum je stav
prostoru, v němž nejsou přítomné žádné částice
látky (jako jsou elektrony, protony a další) ani záření
(fotony). Vytvořit takové dokonalé vakuum je velmi obtížné,
ba v praxi nemožné (nelze se zbavit
např. všudypřítomných neutrin nebo slabě interagujících
masívních částic WIMP tvořících skrytou hmotu ve vesmíru
- §1.5). I kdyby se to podařilo, nebude
se jednat o prázdný prostor kde nic není a
nic se neděje - mohou do něj zasahovat fyzikální pole jako je
elektromagnetické a gravitační (gravitační
pole nelze odstínit). Žádné vakuum
není ve skutečnosti prázdné - podle kvantové teorie pole
tam probíhá mnoho procesů kvantových fluktuací,
neustále vznikají virtuální páry částic a antičástic (viz níže "Kvantová teorie pole").
A už vůbec nelze vakuum (ani to
"dokonalé") považovat za "nicotu"!
Nicota znamená absenci čehokoliv - hmoty, energie, dokonce i
prostoru a času; je to tedy synonimum pro
"neexistenci" - fiktivní filosofický pojem bez
fyzikálního obsahu.
Z filosofického hlediska lze říci, že fyzikální
vakuum není stavem čiré nicoty, ale obsahuje
potencialitu všech forem světa částic (srov.
"Antropický princip aneb
kosmický Bůh").
Vakuum je "živé prázdno" pulzující v nekonečném
rytmu vzniku a zániku struktur, virtuálních a skutečných
částic...
Energie vakua
V klasické (nekvantové) fyzice je hustota
energie samotného vakua (bez polí) nulová.
Zcela okrajovou výjimkou je zde (nekvantová) relativistická
kosmologie, jejíž některé modely zavádějí tzv. kosmologickou
konstantu, která generuje určitou imanentní základní
hustotu energie vakua ve vesmíru (§5.2,
část "Kosmologická konstanta" ve shora zmíněné knize "Gravitace,
černé díry a fyzika prostoročasu").
Podle kvantové teorie pole však
ve vakuu všude a neustále probíhá nesčíslně mnoho procesů
spontánních kvantových fluktuací - neustále
vznikají a zanikají virtuální dvojice částic a
antičástic. Čas trvání těchto fluktuací je
příliš krátký na to abychom tyto částice mohli přímo
detekovat, proto se nazývají virtuální. Fluktuace
kvantových polí mají nejrůznější intenzity a prostorové
rozměry a vzájemně spolu interferují.
Důležitý je výsledek této vlnové interference při
zprůměrování přes čas. Pokud se příspěvky jednotlivých
polních fluktuací v průměru vyruší, bude střední energie
vakua nulová - jedná se o tzv. "pravé
vakuum". Když ale k takovému vyrušení nedojde,
bude střední energie vakua nenulová - takový
stav se nazývá "falešné vakuum".
Podle současné kosmologie mohlo být
"silně falešné" vakuum s vysokou hustotou energie
hnací silou prudké inflační expanze velmi
raného vesmíru (§5.5 "Mikrofyzika
a kosmologie. Inflační vesmír." v knize "Gravitace, černé díry ..."). Současná hodnota vakuové energie je velmi blízká
nule, menší než asi 10-9 J/m3, což odpovídá hmotnostní hustotě asi 10-26 kg/m3. Byly činěny pokusy vysvětlit
energii vakua pomocí kvantové
teorie pole
- jako důsledek kvantových
fluktuací
vakua. Přímočarý výpočet (resp.
dimenzionální odhad), se zahrnutím energie všech
vibračních módů s vlnovou délkou větší než Planckova
délka (10-35m), dává však
nepředstavitelně velkou hustotu energie vakua, odpovídající
hustotě hmotnosti asi 1096 kg/m3..!.. Aby vakuum vypadalo jako
prázdný prostor, musejí se uplatňovat dalekosáhlé kompenzace mezi vakuovými fluktuacemi různých
polí, které naprostou většinu fluktuací vyruší. Tento
"skandální nesoulad" 120 řádů se zatím
nepodařilo uspokojivě vysvětlit; určité naděje snad
slibují unitární teorie pole (§B-.6
"Sjednocování fundamentálních interakcí.
Supergravitace. Superstruny."
ve výše zmíněné knize "Gravitace, černé
díry...").
Pohyb
mikročástic v souborech tvořících hmotu. Termika,
termodynamika.
Než se začneme zabývat vlastnostmi a složením jednotlivých
mikročástic (atomů, molekul, elektronů, atomových jader,
protonů, neutronů, ...), bude užitečné si stručně
povědět o obecných aspektech pohybu těchto částic v souborech
jejich velkého množství, tvořících makroskopickou hmotu.
Každá látka a z ní utvořený systém či těleso se skládá
z částic - molekul, atomů, iontů - které jsou složeny z
menších "elementárních" částic elektronů,
protonů, neutronů. Tyto molekuly, atomy, příp. ionty, jsou v
neustálém neuspořádaném (chaotickém) pohybu v různých
směrech a různými rychlostmi - "tepelném" pohybu. S
rostoucí teplotou (stručně diskutovanou
níže) se zvyšuje rychlost pohybu
částic. Neuspořádaný tepelný pohyb atomů a molekul
způsobuje v látkách několik efektů :
-> Difuze je proces samovolného
rozptylování částic do prostoru a pronikání částic jedné
látky mezi částice druhé látky. Probíhá ochotně
především v plynech a kapalinách, při rozpouštění
pevných látek v kapalinách (např. soli
či cukru ve vodě), v menší míře i
mezi pevnými látkami (pozoruje se na
rozhraní k sobě přitlačených destiček různých kovů). Za vyšší teploty probíhá rychleji.
-> Tlak plynu na stěny nádoby je
vyvolaný nárazy atomů či molekul dopadajících na stěny
nádoby. Se zvyšující se teplotou tlak plynu roste - částice
mají větší rychlost a tím i vyšší kinetickou energii.
-> Tepelná roztažnost pevných látek a
kapalin. Při vyšší teplotě se díky vyšší rychlosti
částic zvětšují jejich vzájemné vzdálenosti, což vede ke
zvýšení objemu látky.
-> Změny elektrické vodivosti kovů,
elektrolytů a polovodičů. V kovech se při vyšší teplotě
zvyšuje intenzita srážek elektronů s atomy krystalové
mřížky, takže elektrický odpor vodiče se s rostoucí
teplotou mírně zvyšuje. Výjimkou je oblast velmi nízkých
teplot jednotky °K, kdy u některých materiálů dochází k
poklesu odporu na nulu, k supravodivosti. V
elektrolytech se naopak při vyšší teplotě zvyšuje disociace
molekul na kationty a anionty, takže elektrická vodivost
elektrolytu se s rostoucí teplotou zvyšuje, elektrický odpor
klesá. Polovodiče se při nízkých teplotách chovají jako
nevodiče; se zvyšující teplotou získávají elektrony
energii a (přes "zakázaný
pás") přeskakují do vodivostního
pásu a mohou se účastnit vedení proudu. S rostoucí teplotou
se zvyšuje koncentrace elektronů a děr a elektrický odpor
polovodičového materiálu se snižuje.
Částice
na sebe navzájem působí přitažlivými i odpudivými silami,
jejichž velikost závisí na vzdálenosti mezi částicemi :
 |
Typická
závislost sil F, působících mezi atomy nebo
molekulami v látkách, na vzdálenosti r. |
Původ těcho sil mezi atomy a molekulami je
elektrický - Coulombovský. I když atomy a molekuly jsou
navenek celkově neutrální, rozložení elektronů je často
nesymetrické, vznikají zde elektrické dipóly. Ty se pak při
vzájemném přiblížení částic polarizují a podle
vzájemné konfigurace dipólových momentů vznikají
přitažlivé nebo odpudivé elektrické síly. Vzájemné
silové působení částic způsobuje, že soustava částic má
svou určitou vnitřní potenciální energii; v případě
přitažlivých sil je to vazebná energie (je
to práce, kterou bychom museli vykonat působením vnějších
sil, aby došlo k rozpadu sil mezi částicemi).
Při
obvyklých teplotách cca 4÷3000 °K se atomy a molekuly v látkách srážejí
pružně, takže látka se chová podle zde
nastíněných zákonů termiky a termodynamiky. Při velmi
nízkých teplotách v blízkosti absolutni nuly dochází u
některých látek ke vzniku Bose-Einsteinový kondenzace, což
může vést ke vzniku supravodivosti a supratekutosti
(§1.5, pasáž "Fermiony v úloze
bosonů; Supravodivost"). Při vysokých teplotách >3000°K je kinetická
energie atomů již natolik vysoká, že při jejich srážkách
dochází k vyrážení elektronů z atomových obalů - k
ionizaaci látky a vzniku plasmy. Zde se již
zásadně uplatňují elektromagnetické vlastnosti elektronů a
iontů (JadRadFyzika3.htm#Plasma). A při nejvyšších
teplotách >1012 °K se již rozbíjejí i atomová jádra a protony a
neutrony na kvarky a gluony - vzniká na okamžik kvark-gluonová
plasma (JadRadFyzika5.htm#KvarkGluonPlasma). Zde jsou
zákonitosti termodynaniky již diskutabilní...
Termika
Neuspořádaný pohyb částic nazýváme tepelný,
neboť podle kinetické teorie stavby látek jsou tyto
mikroskopické pohyby podstatou tepla a
tepelných jevů. Tím se zabývá termika.
Základní fyzikální veličinou, která popisuje tepelný stav
hmoty a její vnitřní energii (měrnou
kinetickou energii chaotického pohybu atomů a molekul), je teplota. Absolutní - termodynamická
teplota T je úměrná střední kinetické
energii neuspořádaného mechanického pohybu částic
hmoty (atomů, molekul) :
< 1/2
m.v2
> = 3/2 kB . T ,
kde m je hmotnost částic, v jejich rychlost
pohybu, kB
je Boltzmannova konstanta udávající vztah mezi
termodynamickou teplotou a vnitřní energii plynu; lomené
závorky < > značí střední hodnotu.
Teplota se obvykle vyjadřuje v jednotkách
zvaných stupně " o ". Teplotní stupně o jsou odvozeny od
tepelně-skupenských vlastností vody. Jeden stupeň
představuje 1/100 teplotního rozdílu mezi teplotou varu vody a
teplotou jejího mrznutí. Takže teplota mrznutí vody (tání
ledu) je 0 oC, teplota varu vody je 100 oC (při atmosférickém tlaku
....). Používají se především dvě
teplotní stupnice. V běžném životě se používají
zmíněné stupně Celsia oC. Ve fyzikální termodynamice se používá
absolutní teplotní stupnice Kelvina *), kde
počáteční-nejnižší teplota T=0 (oK) je teplota "absolutní nuly",
odpovídající -273,15 oC. Teplotní rozdíly v Celsiově a Kelvinově
termodynamické stupnici jsou stejné (Dt=DT), rozdíl je v počátku:
-273,15 oC
= 0 oK
(absolutní nula). Záporné hodnoty v Kelvinech nejsou možné.
Ojediněle se ještě můžeme setkat i s některými dalšími
teplotními stupnicemi (oF -
stupně Fahrenheita, odvozené od normální tělesné teploty,
byly rozšířené především v USA, kde se používají i
nyní; nebo Réumurova stupnice používající teplotu varu
lihu). Převodní vztahy mezi různými stupnicemi jsou uvedeny
ve fyzikálních a chemických tabulkách.
*) Pozn.: U absolutní
teploty v Kelvinově stupnici se označení "o
stupně Kelvina oK" nyní již vynechávají a
vyjadřují se jen jako "Kelviny K". My
v našich materiálech však zápis oK používáme.
Teplota se klasicky měří pomocí teplotní
roztažnosti rtuti či lihu v teploměrech
- tenkých skleněných trubičkách opatřených stupnicí, či
pomocí rozdílné teplotní roztažnosti vrstev bimetalových
pásků. Pro elektronická měření se používá teplotní
závislost elektrického odporu vhodných vodičů a
polovodičů v termistorech. Další možností je
měření intenzity a spektra infračerveného záření
emitovaného zahřátými tělesy.
Termodynamika
Termodynamika se zabývá procesy v látkách souvisejícími s
tepelnými jevy (termikou) především z hlediska dynamiky přenosů
energie a hmoty v rovnovážných a nerovnovážných
systémech, přeměnami tepelné energie na jiné druhy energie,
termodynamikou fázových přeměn, vratnými a nevratnými ději
z hlediska entropie. Z principiálního hlediska je zde
důležité vysvětlení termálních zákonitostí pomocí statistické
fyziky velkého množství částic metodami teorie pravděpodobnosti.
Kromě teploty T je zde důležité i teplo
Q (tepelná energie), což je v termodynamice sumární
kinetická energie všech neuspořádaně se pohybujících
částic - atomů a molekul - v systému či v tělese. Je
součástí vnitřní energie tělesa, do které
se započítává několik složek: především zmíněná
kinetická tepelná energie částic, potenciální
energie atomů a molekul, uvnitř molekul kinetická a
potenciální energie kmitajících atomů, energie elektronů
atomového obalu, jaderná energie, v částicové fyzice a
astrofyzice někdy dokonce klidová energie hmoty podle
Einsteinova vztahu E=m.c2.
Základní jednotka tepelné
energie je Joule (obecně jednotka práce a
energie): 1 J = práce, kterou vykoná síla 1 N působící po
dráze 1 m ve směru pohybu. Někdy se používá starší
jednotka kalorie: 1 cal = energie nutná k ohřátí 1
kg vody o 1 oC (za standard. podmínek, uvádí se 14,5oC). Pro malé energie
v atomové a jaderné fyzice se používá jednotka elektronvolt:
1 eV = 1,602x10-19 J .
Termodynamika, jakožto
ucelená věda o teple a jeho přeměnách, si vybudovala
několik základních postulátů a vývodů - zákonů či
principů termodynamiky, které jsou zobecněním pozorovaných
experimentálních jevů :
1. Rovnovážný stav: Každý
izolovaný systém po uplynutí určité dostatečně dlouhé
doby dospěje do rovnavážného stavu, ve kterém
trvale zůstane (dokud není narušen vnějšími vlivy).
2. Nultý termodynamický zákon:
V rovnovážném systému je teplota ve všech místech v
průměru stejná - je dosažena tepelná rovnováha.
3. První termodynamický zákon:
Energii systému lze změnit jen výměnou tepla Q, mechanické
práce W, nebo polní či chemické energie. Je to tedy zákon
zachování energie v uzavřeném systému, s
možností konání práce a výměny tepla, či přeměn
způsobených excitacemi fyzikálních polí. Energii lze
transformovat z jedné formy na druhou, ale nelze ji vytvořit
či zničit.
4. Druhý termodynamický zákon:
Teplo samovolně nemůže proudít z chladnějšího tělesa do
teplejšího tělesa. Nelze přenášet teplo z chladnějšího
tělesa na teplejší, aniž se přitom určité množství k
tomu potřebné práce změní na teplo. Nelze tedy odnímat
jednomu tělesu teplo a měnit je v užitečnou práci, aniž
přitom určité množství tepla přejde z tělesa teplejšího
na chladnější.
5. Třetí termodynamický zákon:
Nelze dosáhnout termodynamické teploty absolutní nuly
T=0 °K
konečným počtem kroků.
Entropie
Pro vysvětlení a kvantifikaci 2.termodynamického zákona se v
termodynamice vyvinula důležitá veličina entropie
S (řec. en=uvnitř, tropo=změna -
změna uvnitř). V klasické termodynamice tato
veliičina udává změnu tepla Q ve vztahu k teplotě T
podle Clausiova vzorce :
dS = dQ / T ,
kde dS
je změna - zvýšení nebo snížení - entropie, dQ je teplo
předané do systému nebo z něj odvedené a T je
teplota. 2.termodynamický zákon říká, že pro teplo
přenášené jakýmkoli možným procesem do libovolného
systému pro změnu entropie systému platí nerovnost dS >= dQ/T. Uvažuje se zde malé
(infinitezimální) množství dodaného nebo odebraného tepla dQ, při kterém se
téměř nemění teplota T (v
obecném případě, kdy by se teplota měnila, by se provedlo
integrování přes teplotní proměnnou).
Z hlediska termomechaniky entropie též vyjadřuje podíl
tepla nebo energie systému, který nemá schopnost vykonávat
práci.
Ve statistické termodynamice je entropie
definována pomocí počtu mikrostavů, které vedou k danému
makrostavu vyšetřovaného systému - viz níže v pasáži
"Statistická termodynamika". Obě tyto definice
entropie jsou ekvivalentní v tom smyslu, že vedou k 2.zákonu
termodynamiky.
Druhý termodynamický
zákon lze tedy pomocí entropie formulovat jako: V
termodynamicky uzavřené (izolované) soustavě se entropie
nemůže zmenšovat.
Statistická termodynamika
Každý systém - látka, těleso - je tvořen velkým počtem
atomů či molekul, které kmitají a chaoticky se pohybují,
vzájemně se srážejí a odrážejí, pronikají do prostorů
mezi sebou - směšují se. Tento pohyb vytváří teplo. Z
hlediska klasické fyziky se každý atom a molekula musí
řídit Newtonovými zákony mechaniky, takže jejich
pohyby a srážky se v zásadě dají změřit a kvantitativně
analyzovat. Atomů a molekul je zde však obrovské množství a
nedají se měřit a vyhodnocovat každá zvlášť. Zde lze
využít pouze pravděpodobnost - statistickou
mechaniku, která spojuje a průměruje mikroskopické
detaily do makroskopického chování a celkového vyústění.
Mikroskopický stav - zkráceně mikrostav
vyšetřovaného systému představuje detailní znalost přesné
polohy a rychlosti každé částice (atomu, molekuly) v tomto
systému v daném časovém okamžiku. Jelikož se částice
pohybují, vzájemně se srážejí, mění své polohy a
rychlosti, mikrostav se neustále chaoticky mění v průběhu
teplotních fluktuací systému. Každý mikrostav má jen
určitou pravděpodobnost výskytu. Makroskopický
termodynamický popis systému - teplota, tlak, objem,
představuje jeho makrostav. Je mnoho
různých (většinou jen nepatrně
odlišných) mikrostavů, které mohou
globálně poskytovat termodynamicky stejný makrostav systému.
Pokud je systém v rovnovážném stavu, navzdory neustálým
drobným fluktuacím mikrostavu, nedochází k žádným změnám
v jeho makroskopickém termodynamickém chování - nemění se
teplota, tlak, objem.
Ve statistické mechanice se entropie
S systému kvantifikuje jako počet všech mikrostavů,
které by mohly poskytnout výsledný makrostav vyšetřovaného
systému, podle pravděpodobnostního vztahu L.Boltzmanna :
S = kB
. ln W ,
kde S je termodynamická entropie, W je počet
všech mikrostavů které mohou poskytnout daný termodynamický
makrostav. Konstanta kB = 1,38049×10-23 Joulů na Kelvin je Boltzmannova konstanta mezi průměrnou tepelnou
energií částic v plynu a termodynamickou teplotou tohoto
plynu. Konstanta úměrnosti kB slouží k tomu, aby
se hodnota entropie ve statistické mechanice rovnala klasické
termodynamické entropii v Clausiově vzorci.
Pozn.:
Přirozený logaritmus ln W se používá v matematické
statistice, kde kvantifikuje informační entropii náhodné
proměnné v systému.
Příklad
takového makroskopického chování si můžeme představit v
jednoduchém experimentu: Vezmeme nádobu s
plynem, která je rozdělena na dvě části, oddělené
přepážkou (podobné jako na obrázku
"Maxwellův démon" níže). Do
jedné části napustíme plyn nebo kapalinu s vyšší teplotou (molekuly se v něm pohybují vyšší rychlostí, s
vyšší kinetickou energií) než v druhé
části. Když přepážku odstraníme, molekuly se začnou
mísit - rychlé molekuly difundují a narážejí do
pomalejších. Dochází k výměně kinetické energie a po
určité době plyn či kapalina dosáhne rovnováhy se stálou
průměrnou teplotou. To je všeobecně známá zkušenost, v
praxi to nikdy nedopadne jinak.
Newtonovy pohybové rovnice jsou invariantní
vzhledem k obrácení směru času. Pokud se v
dynamickém systému ve stejném čase přesně obrátí pohyb
jeho každé částice, pak se všechno bude dít pozpátku.
Pokud pozorujeme pohyby jednotlivých atomů a molekul v
mikroskopických detailech, chovají se stejně když je
sledujeme v čase směrem dopředu nebo zpět (podobně jako
když film si promítneme dopředu či pozpátku). Když ale
budeme sledovat nádobu s plynem či tekutinou, proces
směšování se makroskopicky stane časově jednosměrným.
Nikdy se nedočkáme toho, že by se v plynu či kapalině atomy
rozdělily na teplé na jedné straně a studené na druhé
straně. Nemůžeme je od sebe oddělit, pokud čas běží
dopředu a nikdy se nevrací.
Důvodem takové jednosměrnosti procesů je pravděpodobnost
- statistika. Obecně počet neuspořádaných stavů je
nesrovnatelně větší než počet stavů uspořádaných.
2.termodynamický zákon je tedy statistickýn důsledkem
skutečnosti, že neuspořádaných stavů je mnohem více než
stavů uspořádaných....
"Maxwellův démon"
třídíci částice ?
Ve fundamentální fyzice by v zásadě nic nemělo zabránit
částicím uspořádat se v různých rovnoměrných i
nerovnoměrných konfiguracích. Nic by tedy nemělo zabránit
plynu aby se rozdělil na chladnou a teplou část, je to pouhá
statistická náhodnost. J.C.Maxwell navrhl následující
myšlenkový experiment :
Vezmeme dvě baňky spojené trubičkou s
oddělující přepážkou, která se dá zavřít nebo otevřít
pomocí ventilu (např. s šoupátkem). Při uzavřené
přepážce napustíme do levé baňky plyn sestávající ze
dvou druhů atomů, nebo z atomů rychlejších (červené) a
pomalejších (modré) - obr.a). Pravá baňka je prázdná, je tam
vakuum. Když se pak přepážka trvale otevře, v
důsledku chaotického pohybu difuzí pronikne i do druhé
nádoby v průměru stejné zastoupení obou druhů částic,
jaké je v levé nádobě (b).
Pokud by ale v oddělující
přepážce byl ventil, který by se mohl střídavě otvírat a
zavírat, daly by se pomocí něho částice pronikající do
baňky vpravo "třídit". Představme si, že tento
ventil by ovládala nějaká velmi rychlá a pozorná bytost s
nekonečně subtilními smysly - "démon", který by
uměl u difundujících částic rozpoznat zda jsou rychlé či
pomalé a mohl se rozhodnout, zda je nechá ventilem projít (c). Mohl by do druhé baňky
propustit jen např. rychlejší (červené) částice, zatímco
pomalejší (modré) částice by zadržel uzavřením
přepážky, od které by se odrazily zpět. Démon takto
nahrazuje náhodu účelem. V konečném důsledku (po dostečné
době) by v levé baňce zůstaly jen "modré"
částice a v pravé baňce by byly jen "červené"
částice (d). Tím by
porušil běžnou pravděpodobnost, podle níž by se
všechny částice měly promíchat.
 |
| "Maxwellův démon" schopný
třídít částice. a) Výchozí situace: dvě baňky spojené trubičkou s oddělující přepážkou. Baňka vlevo je naplněna plynem či kapalinou sestávající ze dvou druhů částic. b) Když se přepážka otevře, v důsledku chaotického pohybu difuzí pronikne i do druhé nádoby v průměru stejný počet obou druhů částic, jaký je v levé nádobě. c) Pokud by v přepážce byl ventil, který by střídavě otvíral a zavíral "démon" který je schopen rozpoznat difundující částice, mohl by do druhé baňky propustit jen např. rychlejší (červené) částice, zatímco pomalejší (modré) částice by zadržel uzavřením přepážky, od které by se odrazily zpět. d) V konečném důsledku (po dostečné době) by v levé baňce zůstaly jen "modré" částice a v pravé baňce by byly jen "červené" částice. |
Maxwellův démon při třídění částic v idealizovaném
případě sice nemusí vykonávat žádnou práci při
otvírání a zavírání ventilu, avšak při rozhodování
využívá informaci, která není volně dostupná -
"není zadarmo"! Informace má fyzikální podstatu.
Zde se jedná o informace o rychlostech a trajektoriích
jednotlivých částic. Pokaždé, když se démon rozhodne mezi
dvěma částicemi (o jejich propuštění či zadržení),
stojí to jeden bit informace. Každá jednotka
informace pak přináší odpovídající nárust entropie s
konverzním faktorem kB.log2. To
obnovuje soulad s 2.termodynamickým zákonem.
"Maxwellův démon" je samozřejmě jen
fikce a reálně neexistuje. Jeho třídící úlohu pro
atomy a molekuly však v přírodě za určitých okolností
vykonávají některé fyzikálně-chemické a biologické
procesy. Živé buňky při své funkci, růstu, rozmnožování
vytvářejí složité uspořádané struktury - jako by
vzdorovaly 2.termodynamickému zákonu. Buňka však není
izolovaným systémem, takže část energie, používané ke
svým vnitřním procesům, mění v teplo, které se rozptyluje
do okolí buňky a zvyšuje v něm neuspořádanost. Takže
bilance celkové entropie buňky a okolí se mění v souladu s
termodynamickými zákony. Membrány buněk vykazují
často jednosměrnou propustnost a jsou schopny regulovat
rozdíly v koncentracích iontů, při spotřebě energie. Enzymy
mohou působit též jednosměrně a mohou být metastabilní -
po deaktivaci se jejich energie rozptyluje, mění v teplo a
zvyšuje entropii v okolí. Při metabolismu se buňky a
organismy úspěšně zbavují entropie, nutně vytvářené
během jejich životního fungování.
Býložravci a masožravci se živí organickými
látkami, které jsou ve značně uspořádaním stavu a vrací
je do přírody značně znehodnocené. Ale ne úplně, dokážou
ho částečně využít ještě rostliny, které navíc ze
slunečního záření získávají nejen energii, ale i
negativní entropii. Zkrátka "organismy organizují" a
vysávají přitom "negativní entropii" se svého
okolí; a to ji získává ze slunečního záření.
Ostatně, největšími
"bojovníky" proti entropii a 2.termodynamickému
zákonu jsme patrně my lidé. Kromě biologických procesů v
našem těle neustále něco třídíme, sbíráme,
shromažďujeme, píšeme literaturu, poznáváme přírodu a
vesmír, skládáme hudbu, kreslíme obrazy, uklízíme v bytě,
... atd. A lidská civilizace buduje kolosální výtvory s
přesnou strukturou ...
O vztahu entropie a života je stručně
diskutováno v pasáži "Může fungování života a jeho evoluce
porušovat 2.zákon termodynamiky?" práce "Antropický princip aneb
kosmický Bůh".
Všechny nevratné
procesy mají stejné fyzikálně-matematické
vysvětleni: pravděpodobnost. Druhý
termodynamický zákon je pouze pravděpodobnostní. Statisticky
všechno směřuje k nejvyšší entropii. Čistě fyzikálně
vzato není nemožné, aby se atomy či molekuly v nádobě s
plynem nesmísily a zůstaly oddělené - je to jen mimořádně
nepravděpodobné. Nepravděpodobnost toho, že teplo přejde
samovolně (bez vnější pomoci) z chladnějšího tělesa na teplejší, je podobná
jako nepravděpodobnost samovolného uspořádání řádu z
chaosu. Obě tyto nepravděpodobnosti mají statistický
charakter. 2.termodynamický zákon znamená sklon
fyzikálních soustav částic plynout od méně
pravděpodobných - uspořádaných - makrostavů k
pravděpodobněšjším - neuspořádaným.
Zákonitosti
termodynamiky hrají důležitou úlohu v chování látek v
přírodě, složených z atomů a molekul - v našem
makroskopickém světě. Termodynamické koncepce však byly
zobecněny i na jiné jevy v mikrosvětě a ve vesmíru
- viz např. §4.7 "Kvantové
vyzařování a termodynamika černých děr", nebo §5.6 "Budoucnost vesmíru. Temná hmota. Temná
energie.", pasáž "Šipka
času" v monografii "Gravitace, černé díry a
fyzika prostoročasu".
Zamyšlení nad kauzalitou a náhodností v přírodě a vesmíru
je v §3.3, pasáži "Determinismus,
náhoda, chaos?".
Elektromagnetické pole a záření
Než se začneme věnovat stavbě
atomů a jevům probíhajícím uvnitř, bude užitečné
povědět si pár slov o jednom z nejdůležitějších
fenoménů v přírodě - o elektromagnetickém
působení a elektromagnetickém záření. S
elektromagnetickou interakcí jsou totiž úzce spojeny i
veškeré události v atomech a jejich jádrech.
Každý elektrický náboj Q
budí kolem sebe elektrické pole o intenzitě E,
úměrné (podle Coulombova zákona) velikosti náboje Q
a nepřímo úměrné druhé mocnině vzdálenosti r : E
= ro . k. Q/r2, kde ro je jednotkový vektor směřující od náboje Q do
vyšetřovaného místa a k je koeficient vyjadřovaný v
soustavě jednotek SI pomocí permitivity vakua eo: k = 1/4peo. Pokud se náboj
nepohybuje (v dané vztažné soustavě), jedná se o pole elektrostatické. Toto
elektrické pole působí silovými účinky F
= q.E na každý jiný náboj q, který se do
tohoto prostoru dostane. Elektrické pole je obecně zřídlové,
jeho zdrojem jsou elektrické náboje ze kterých vycházejí ("pramení") a do nichž
vcházejí elektrické siloočáry. Avšak za
nepřítomnosti elektrických nábojů, pokud je elektrické pole
buzeno elektromagnetickou indukcí při časových změnách
magnetického pole (jak je zmíněno níže), může být
elektrické pole nezřídlové.
Jaké nejsilnější
může být elektrické pole?
V rámci klasické (nekvantové) fyziky může být elektrické
pole ve vakuu libovolně silné, až téměř k nekonečnu (v látkovém prostředí je to však omezeno
elektrickou pevností dielektrika). Z
hlediska kvantové elektrodynamiky však i ve vakuu
existuje principiální omezení, způsobené existencí
vzájemných antičástic elektronu a pozitronu:
nelze vytvořit elektrické pole o intenzitě silnější než Ee-e+ = me2c3/e.h = 1,32.1016 V/cm, kde me je klidová hmotnost
elektronu či pozitronu. Při překročení této intenzity je
totiž gradient potenciálu vyšší než prahová energie 2mec2 a dochází ke vzniku dvojice elektronu a
pozitronu, která intenzitu elektrického pole
automaticky zredukuje. Tak silné elektrické pole se zatím
nepodařilo vytvořit, klasickou elektronikou to není možné;
určitou možností v budoucnosti by mohly být silné impulsy z
extrémně výkoných laserů...
Jestliže se náboj Q
pohybuje (elektrický proud), budí kolem sebe kromě
elektrického ještě pole magnetické.
Pohybující se náboje, vytvářející v délkovém elementu dl
proud I, vzbuzují ve vzdálenost r magnetické
pole o intenzitě B (nešťastně
zvané z historických důvodů magnetická indukce) podle Biot-Savart-Laplaceova zákona: dB
= k . I .[dl´ro]/r2, kde ro je jednotkový směrový vektor od měřeného místa k
proudovému elementu a k je konstanta úměrnosti
vyjadřovaná v soustavě jednotek SI pomocí tzv. permeability
vakua mo: k = mo/4p. Magnetické pole vykazuje silové účinky na každý
elektrický náboj q pohybující se rychlostí v:
F = q.(B´v); tato
tzv. Lorentzova síla působí kolmo na směr pohybu
náboje. Magnetické pole je (na rozdíl od
pole elektrického) vždy nezřídlové,
magnetické siločáry jsou uzavřené křivky - neexistují tzv.
magnetické monopóly (magnetické "náboje",
obdoba elektrických nábojů).
Při pohybu nebo časových změnách v
magnetickém poli vzniká podle Faradayova zákona elektromagnetické
indukce pole elektrické - ve tvaru jakéhosi
"víru", krouživého elektrického pole kolem
proměnného magnetického pole. Indukované elektrické pole
může způsobit pohyb nábojů, např. elektronů ve vodiči - indukovaný
elektrický proud. A časové změny pole elektrického
vyvolávají zase pole magnetické (jako
kdyby protékal tzv. Maxwellův posuvný proud), opět vírového charakteru. Tato dialektická jednota
elektrického a magnetického pole nachází své uplatnění v
koncepci elektromagnetického pole, jehož
speciálními projevy je pole elektrické a magnetické. Toto
pole se řídí Maxwellovými rovnicemi
elektromagnetického pole, které vznikly sloučením a
zobecněním všech zákonitostí elektřiny a magnetismu.
Sloučená nauka o elektřině a magnetismu, zahrnující
dynamiku pohybů nábojů a časové proměnnosti polí, se
nazývá elektrodynamika.
Pozn.: Podrobnosti
o teorii elektromagnetického pole lze nalézt např. v §1.5 "Elektromagnetické
pole. Maxwellovy rovnice"
knihy "Gravitace, černé díry a fyzika
prostoročasu".
Níže, v části "Atomová struktura hmoty" uvidíme, že elektromagnetické síly mají
určující význam pro stavbu atomů a pro jejich vlastnosti - určující
význam pro stavbu hmoty na mikroskopické i
makroskopické úrovni, včetně všech jevů chemických. Spolu
se silnými interakcemi pak hrají elektrické síly důležitou
roli i ve stavbě atomových jader (jak uvidíme v části "Struktura atomového jádra") a při excitacích a
deexcitacích jejich vzbuzených energetických stavů.
Elektromagnetické
vlny
Maxwellovy rovnice mají řadu pozoruhodných vlastností, pro
nás je zde však důležitá následující zákonitost: Rozruch
(změna) v elektromagnetickém poli se v prostoru šíří
konečnou rychlostí rovnou rychlosti světla. Jestliže
se elektrické náboje pohybují proměnnou rychlostí
(nerovnoměrně, se zrychlením), vytvářejí kolem sebe
časově proměnné elektromagnetické pole, což vede ke vzniku elektromagnetických
vln, které se odpoutávají od svého zdroje a
odnášejí s sebou do prostoru část jeho energie.
Elektromagnetické pole se pak dále šíří prostorem již
nezávisle na zdrojových elektrických nábojích a proudech ve
formě volné elektromagnetické vlny - je odvozeno v §1.5, část "Elektromagnetické vlny" již zmíněné knihy "Gravitace,
černé díry a fyzika prostoročasu".
Z Maxwellových rovnic lze vhodnou úpravou
dojít k dvěma parciálním diferenciálním rovnicím pro
vektory E a B :
¶2E/¶x2 + ¶2E/¶y2
+ ¶2E/¶z2
= e.m .¶2E/¶t2 , ¶2B/¶x2
+ ¶2B/¶y2
+ ¶2B/¶z2
= e.m .¶2B/¶t2 ,
což jsou vlnové rovnice popisující šíření
časově proměnného elektrického a magnetického pole v
prostoru rychlostí c = Ö(1/e.m), kde e je elektrická permitivita a m je magnetická permeabilita
daného prostředí: E(x,y,z,t) = f(t - x/c) a
analogicky pro B, uvažujeme-li pro jednoduchost
vlnění šířící se ve směru osy x. Nejčastěji se uvažuje
harmonická (sinusová resp. kosinusová)
časová závislost: E(x,y,z,t) = Eo.cos(w.(t - x/c)) a
analogicky pro B, kde w = 2pf je kruhová frekvence.
Vlnění totiž často vzniká v důsledku periodických
kmitavých pohybů elektrických nábojů (např. v
anténách napájených vysokofrekvenčním signálem o frekvenci
f); i v případech, kdy tomu tak není (např. brzdné
záření) lze vznikající vlnění Fourierovsky rozložit
na harmonické složky o různých frekvencích a
fázích.
Největší rychlosti dosahuje elektromagnetické vlnění ve
vakuu, kde je co = 1/Ö(eo.mo) = 2,998.108m/s @ 300 000 km/s. V látkovém prostředí,
jehož permitivita a permeabilita jsou větší než pro vakuum,
je rychlost elektromagnetického vlnění poněkud nižší
- u světla to vede ke známým optickým jevům lomu
světelných paprsků při přechodu světla mezi
látkami s různou optickou hustotou (viz níže "Elektromagnetické
a optické optické vlastnosti látek").
Elektromagnetické vlnění je tedy podle
Maxwellových rovnic elektrodynamiky příčným
vlněním elektrického a magnetického pole (vzájemně
se budícího svou proměnností), kde vektor E
elektrické intenzity a vektor B magnetické
indukce kmitají s amplitudou A neustále kolmo
k sobě a kolmo ke směru šíření vlny (viz horní část
obr.1.1.1), které ve vakuu probíhá rychlostí světla c=300
000 km/s. Elektromagnetické vlny v praxi nejčastěji vznikají
při vibracích elektrických nábojů, resp.
vibračním pohybu elektricky nabitých částic jako jsou
elektrony nebo ionty.
A zase naopak, elektromagnetická vlna periodicky
silově působí na elektricky nabité částice - ve
vodičích uvádí elektrony do pohybu a indukuje v nich
střídavý elektrický proud; na tom je založen příjem
elektromagnetického vlnění anténou. Periodičnost v
prostoru je dána vlnovou délkou, periodičnost v čase
pak frekvencí. Intenzita (síla, mohutnost)
elektromagnetické vlny je dána amplitudou kmitající
elektrické intenzity E a magnetické indukce B,
přenos energie tzv. Poyntingovým vektorem. Mezi
rychlostí světla c, frekvencí kmitání n a vlnovou
délkou l platí jednoduché vztahy: l = c/n, n = c/l, l.n = c. Čím vyšší je
frekvence kmitání elektromagnetického pole, tím kratší je
vlnová délka. A právě na této frekvenci či
vlnové délce podstatně závisejí vlastnosti
elektromagnetických vln.
Pozn.: Vznik
a šíření vln v látkových prostředích a především
fyzikálních polích je obecný fundamentální
přírodní jev - je analyzováno v úvodní části
§2.7 "Šíření vln - obecný přírodní fenomén" již zmíněné knihy "Gravitace,
černé díry a fyzika prostoročasu".
Elektromagnetické vlny v atomové a jaderné
fyzice
Obecná zákonitost elektrodynamiky, že časové změny
elektrického a magnetického pole jsou schopny se v prostoru
šířit jako elektromagnetické vlny přenášející
energii, hraje významnou roli v atomové, jaderné a
radiační fyzice. V prvé řadě je to elektromagnetické záření
atomů při přeskocích elektronů mezi energetickými
hladinami v elektrickém poli jádra (viz
níže "Záření atomů"). Dále je to brzdné
záření vznikající obecně při zrychleném pohybu
elektrických nábojů, v radiační fyzice především při
dopadu rychlých elektronů na látku a jejich rychlém
zbrzdění při interakci s atomy látky (§1.6, část "Interakce nabitých částic"). Subtilnějšími
radiačními efekty jsou Čerenkovovo záření
a přechodové záření, vznikající při průletu
rychlých nabitých částic látkovým prostředím (§1.6, pasáž "Čerenkovovo záření"). V oblasti atomových
jader je to deexcitace jaderných hladin vyzářením
elektromagnetického záření - fotonů záření gama
(§1.2, část "Záření
gama").
Rozdělení
elektromagnetického záření
Podle vlnové délky či frekvence rozdělujeme
elektromagnetické vlny na několik skupin :
Poslední dva druhy krátkovlnného záření, X a gama, se svými spektry (vlnovými délkami či energiemi) částečně prolínají a vyskytují se zde někdy terminologické nejasnosti. Ve zmíněném §1.2, část "Záření gama", je terminologická dohoda o členění krátkovlnného elektromagnetického záření podle jeho původu - záření gama pochází z jádra, záření X z ostatních oblastí atomu mimo jádro.
Jednotky
energie, hmotnosti a náboje v atomové a jaderné fyzice
Ve většině oblastí fyziky a přírodovědy se používá soustava
jednotek SI, v nichž základními jednotkami jsou: metr
[m] jako jednotka délky, sekunda [s] jako
jednotka času a kilogram [kg] pro hmotnost;
často jsou používány dekadické násobky - centimetr či gram
atd. Základní jednotkou práce a energie je joule
[J], jednotkou elektrického náboje coulomb
[C].
V atomové a jaderné fyzice, která zkoumá jevy v malých
prostorových měřítcích a velmi malých hodnotách absolutní
energie a náboje, se ustavily některé poněkud odlišné
zvyklosti v používaných jednotkách hmotnosti,
energie a náboje. Tyto alternativní jednotky jsou
lépe "šité na míru" zkoumaným jevům v mikrosvětě,
než jednotky SI pocházející z makroskopických jevů.
Jednotka času sekunda je ponechána,
jednotka délky, metr či centimetr, je
většinou rovněž ponechána (samozřejmě s použitím
dekadických zlomků 10-xx); někdy se používá jednotka angström:
1A° = 10-10m = 10-8cm (v atomové fyzice
je to typický rozměr atomu), nebo fermi: 1fm =
10-15m =
10-13cm (femtometr,
v jaderné fyzice je to charakteristický rozměr jádra).
Jako jednotka energie se v atomové fyzice
nepoužívá příliš velký 1Joule, nýbrž 1 elektronvolt,
což je kinetická energie, kterou získá náboj jednoho
elektronu v elektrickém poli při urychlení potenciálovým
rozdílem jednoho voltu: 1eV = 1,602.10-19J.
V jaderné fyzice, kde jsou vyšší energie a energetické
rozdíly, pak dekadické násobky - kiloelenktronvolt (1keV=103eV), megaelektronvolt
(1MeV=106eV)
a gigaelektronvolt (1GeV=109eV).
Rovněž obvyklá jednotka hmotnosti, kilogram
či gram, je pro atomovou a jadernou fyziku neprakticky
veliká. Pod hmotností se v jaderné fyzice zpravidla rozumí klidová
hmotnost částic a je zvykem ji vyjadřovat v energetických
jednotkách na základě Einsteinova vztahu E =
m.c2 ekvivalence hmotnosti a energie, tedy rovněž v elektronvoltech:
1eV = 1,783.10-33gramu; a samozřejmě v jejich dekadických násobcích.
Klidovou hmotnost elektronu můžeme tedy
vyjádřit jako: me = 9,1.10-28g = 511 keV.
Hmotnost těžších elementárních částic se kromě [MeV]
někdy vyjadřuje i v násobcích hmotnosti elektronu
me -
např. hmotnost protonu můžeme vyjádřit třemi různými
způsoby: mp = 1,673.10-24g = 938 MeV
= 1836 me.
Pro elektrický náboj se místo příliš
velké jednotky Coulomb používá jako přirozené
základní jednotky náboj elektronu e, resp.
stejně velký ale opačný náboj protonu,
který je elementárním elektrickým nábojem: e = 1,602.10-19Coulombu.
Ze soustavy SI však vycházejí nyní používané
jednotky dozimetrických veličin,
charakterizujících účinky ionizujícího záření na látku
a živou tkáň. Jedná se zde totiž o kumulativní účinky
makroskopického charakteru. Základní veličinou je zde absorbovaná
radiační dávka, jejíž jednotka je 1Gray
= 1J/1kg (podrobněji viz §5.1 "Účinky záření na látku. Základní veličiny
dozimetrie.").
Poznámka k
veličinám a jednotkám v jaderné fyzice
Terminologie, veličiny a jednotky související s atomy, jádry,
radioaktivitou a radioaktivním zářením, prošly dlouhým a
spletitým vývojem, který zanechal některé nelogičnosti a
nejednoznačnosti - bude upřesněno níže. Ostatně, podobné
gnoseologické nekonzistentnosti se v důsledku historického
vývoje vyskytují i v jiných fyzikálních oborech. Vzpomeňme
např. nešťastné zavedení elektrického proudu jako
základní veličiny a jeho SI jednotky 1Ampér (pomocí
"silového působení dvou nekonečných rovnoběžných
vodičů..."), zatímco fyzikálně primární elektrický
náboj (a jednotka Coulomb) je zaveden jako odvozený z proudu.
Nebo v magnetismu terminologická nelogičnost názvů
"intenzita magnetického pole" a "magnetická
indukce" (u elektrického pole je to přitom v pořádku)...
Exkurze
do vysokých rychlostí - speciální teorie relativity
Mikročástice, z nichž je
složena hmota, se při procesech uvnitř atomů, atomových
jader a při vzájemných interakcích pohybují většinou velmi
vysokými rychlostmi, blížícími se často
rychlosti světla. Při experimentech s těmito velkými
rychlostmi bylo zjištěno, že zde již přestávají platit
obvyklé zákonitosti klasické Newtonovy mechaniky.
Albert Einstein ve svých výzkumech na počátku 20.stol.
navázal na Galileiho a Newtonovu klasickou mechaniku, Maxwellovu
elektrodynamiku a na výzkumy svých předchůdců (Lorentz,
Michelson-Morley, ...) a vytvořil novou mechaniku - tzv. speciální
teorii relativity, zobecňující klasickou mechaniku i
na pohyby vysokými rychlostmi blízkými rychlosti světla.
Systematický výklad této jistě zajímavé teorie zde není
možné uskutečnit; lze jej najít v řadě knižních
publikací (na těchto stránkách je to
např. §1.6 "Čtyřrozměrný prostoročas a speciální
teorie relativity" v
knize "Gravitace, černé díry a fyzika prostoročasu"). Zde si jen stručně
připomeneme některé základní jevy speciální teorie
relativity, které mají zásadní důležitost při jaderných
procesech a interakcích elementárních částic.
Speciální teorie relativity (STR) je založena na dvou
základních postulátech:
Relativistická
kinematika
Z těchto dvou experimentálně dokonale ověřených principů
plyne, že vztahy mezi polohovými souřadnicemi a časovými
intervaly událostí v různých inerciálních vztažných
soustavách se zákonitostmi klasické kinematiky řídí jen
při malých rychlostech, zatímco obecně se řídí tzv. Lorentzovými
transformacemi
x´ = (x - V.t)/Ö(1-V2/c2) , y´ = y , z´ = z , t´ = (t - x.(V/c2))/Ö(1-V2/c2) ,
udávajícími vztah mezi prostorovými souřadnicemi x,y,z a
časem t v inerciální soustavě S a v soustavě S´
pohybující se vzhledem k S rychlostí V ve směru
osy x.
Pozn.: V nerelativistické fyzice je vztah mezi těmito
souřadnicemi dán jednoduchou Galileiho transformací
x´= x -V.t, y´= y, z´= z, t´= t (čas zde samozřejmě teče
stejně rychle!).
Z Lorentzových transformací plynou
důležité kinematické efekty speciální
teorie relativity:
Kontrakce délek:
Rozměr l každého tělesa (vlastní)délky lo, které se pohybuje
rychlostí v, se ve směru pohybu jeví zkrácený ve
srovnání se svým klidovým rozměrem lo: l = lo.Ö(1-v2/c2).
Dilatace času:
Čas na pohybujícím se tělese teče vzhledem k času
vnějšího klidového pozorovatele tím pomaleji, čír rychleji
se těleso pohybuje: Dt = Dt .Ö(1-v2/c2). Dt je čas měřený vnějšími klidovými hodinami, Dt je vlastní
čas měřený hodinami pohybujícími se spolu s tělesem
rychlostí v.
Einsteinův zákon skládání rychlostí:
Pohybuje-li se jedno těleso rychlostí v1 a druhé těleso vzhledem k němu rychlostí v2 ve stejném směru,
pak vzhledem k výchozí inerciální vztažné soustavě bude
výsledek složení obou rychlostí v = (v1+v2)/(1+v1.v2/c2), a nikoliv v1+v2, jak by tomu bylo v klasické mechanice.
Z uvedených kinematických efektů speciální teorie
relativity má pro jadernou a částicovou fyziku značný
význam zejména dilatace času, díky níž
částice s krátkou dobou života mohou žít
mnohonásobně déle, pokud se pohybují rychlostí
blízkou rychlosti světla. Díky tomuto efektu např. m-mezony (s dobou
života 2.10-6sec) vzniklé interakcí kosmického záření ve
vysokých vrstvách atmosféry stačí doletět až k povrchu
země, kde je můžeme pozorovat. Nebo můžeme mezony p+, p-,
vzniklé při interakcích vysokoenergetických protonů z
urychlovače, vyvádět ve svazcích a studovat jejich interakce
po dobu mnohonásobně delší než je jejich klidová doba
života 2,6.10-8sec.
Relativistická
dynamika
Spojením relativistické kinematiky STR a (Newtonovy) dynamiky
pohybů těles vzniká relativistická dynamika,
jejímž základním novým zjištěním je, že (setrvačná)
hmotnost těles m není konstantní, ale hmotnost
závisí na rychlosti tělesa v podle
důležitého vztahu
m = mo/Ö(1-v2/c2) ,
kde mo je klidová
hmotnost tělesa *), kterou má v inerciální vztažné
soustavě v níž je v klidu. Hmotnost tělesa tedy roste
s rychlostí, a to zvláště když se rychlost blíží
rychlosti světla - pak hmotnost tělesa roste teoreticky k
nekonečnu: limv®c m = Ą.
Dalším důležitým výsledkem relativistické dynamiky je
vztah pro celkovou energii tělesa o klidové
hmotnosti mo pohybující se rychlostí v:
E = mo.c2/Ö(1-v2/c2)
a z něj plynoucí poznatek o ekvivalenci hmotnosti a
energie vyjádřený slavným Einsteinovým vztahem E =
m . c2 ; resp. DE = Dm . c2 .
Oba tyto vztahy závislosti hmotnosti na rychlosti i
ekvivalence změn hmotnosti a energie hrají kardinální úlohu
v jaderné a částicové fyzice, kde dochází k vzájemným
přeměnám energií a částic pohybujících se vysokými
rychlostmi.
*) Tento vztah nelze přímo použít pro
částice s nulovou klidovou hmotností (mo=0) pohybující se
rychlostí světla v=c - takovými částicemi jsou především
kvanta elektromagnetického vlnění - fotony.
Foton má energii E = h.n, danou jeho frekvencí n a lze mu připsat
(relativistickou) setrvačnou hmotnost m = E/c2 = h.n/c2.
Obecná
teorie relativity
Vedle speciální teorie relativity vytvořil Einstein i obecnou
teorii relativity, která je sjednocenou relativistickou
fyzikou gravitace a prostoročasu.
Tou se zde nebudeme zabývat, neboť v atomové a jaderné fyzice
se gravitační interakce neuplatňuje (pomineme-li zatím
unitární teorie pole...). Tato velmi zajímavá teorie je
podrobně vykládána v monografii "Gravitace,
černé díry a fyzika prostoročasu",
především v kapitole 2 "Obecná teorie relativity - fyzika
gravitace", spolu s jejími
důsledky v astrofyzice a kosmologii - kapitola 4 "Černé díry" a kapitola 5 "Relativistická
kosmologie".
Korpuskulárně-vlnový
dualismus
V klasické fyzikce i v běžném životě pozorujeme
diametrální rozdíl mezi diskrétními částicemi
nebo tělesy s jejich pohyby popsanými klasickou mechanikou, a
mezi kontinuálním vlněním šířícím se v
určitém prostředí. V mikrosvětě ovládaném zákonitostmi
kvantové fyziky se však za určitých okolností tento rozdíl
stírá !
Korpuskulární
vlastnosti vlnění
Na přelomu 19. a 20.stol. fyzika vysvětlovala
přírodní jevy buď pomocí částic, nebo
pomocí elektromagnetického pole a jeho
vlnění - elektromagnetického záření,
jehož speciálním druhem je světlo. Prakticky
všechny v té době známé vlastnosti světla v optice
(zákonitosti šíření, odraz, lom, ohyb světla, interference)
se daly velmi dobře vysvětlit vlnovou
představou. Zdálo se, že Huyghensův vlnový přístup k
záření zcela zvítězil nad Newtonovou korpuskulární
představou. Některé v té době nedávno objevené vlastnosti
záření se však čistě vlnovou představou nedaly úplně
uspokojivě vysvětlit.
Záření černého
tělesa
Prvním takovým jevem bylo spektrum záření zahřátého ("absolutně") černého
tělesa *), které v r.1900 podrobně prozkoumal M.Planck. Pro
vysvětlení pozorovaného tvaru spektra záření černého
tělesa jako funkci jeho teploty Planck vyslovil hypotézu, že
vyzařování (i pohlcování) elektromagnetického záření
jednotlivými atomy v tělese se neděje plynule a spojitě, ale
po určitých malých přesných dávkách - kvantech
energie. Zdroje elektromagnetického záření lze považovat za oscilátory,
které nemohou kmitat s libovolnou frekvencí a energií, ale
vyzařují či pohlcují energii jen v určitých kvantech.
Velikost energie E těchto kvant je závislá pouze na frekvenci
záření n a Planck pro ni stanovil vztah E = h.n, kde konstanta
úměrnosti h @ 6,626.10-34J/s byla nazvána Planckova konstanta.
Planck samotný považoval zpočátku tento předpoklad pouze za
pracovní hypotézu ad hoc (jakýsi
přechodný "trik v nouzi", jak vysvětlit
nesrovnalosti ve spektru), která by měla
být později nahrazena přijatelnějším vysvětlením. Ve
skutečnosti se však tato hypotéza ukázala správná a stala
se počátkem nového pojímání mikrosvěta - kvantové
fyziky.
*) Každé těleso (složené z látky
jakéhokoli skupenství), zahřáté na teplotu vyšší než
absolutní nula, emituje elektromagnetické záření - tepelné
záření, vznikající při kmitání a srážkách
elektronů, atomů a molekul v důsledku jejich termických
pohybů. Toto záření odnáší část tepelné energie
dodávané tělesu zvnějšku, nebo generované uvnitř tělesa.
Pro modelové studium tepelného vyzařování se zavádí tzv. absolutně
černé těleso, které pohlcuje veškeré záření jež na
ně dopadá. Dá se realizovat uzavřenou krabicí se
zahřátými vnitřními stěnami opatřenou malým otvorem,
kterým tepelné záření uniká do vnějšího prostoru.
V r.1879 objevili Stefan a Boltznan vyzařovací zákon pro
intenzitu záření černého tělesa v závislosti na teplotě:
I = s .
T4, kde s = 5,67.10-8 W.m-2.K-4 je
Stefan-Boltzmanova konstanta. Pro určení vyzařovaného spektra
tepelného záření se však nedařilo najít uspokojivý a
jednotný zákon. Byly formulovány dva zákony pro vyzařované
spektrum, které však s experimentálně změřenou spektrální
křivkou souhlasily pouze částečně: Rayleigh-Jeansův
zákon dobře popisoval spektrum v oblasti dlouhých
vlnových délek, ale nesouhlasil (dokonce
divergoval) v oblasti krátkých vlnových
délek; Wienův zákon se choval naopak. Sjednotit obě
spektrální oblasti se podařilo M.Planckovi, který objevil
nový vyzařovací zákon, který byl v naprostém souladu s
experimenty ve všech spektrálních oblastech.
Fotoelektrický
jev
Dalším jevem, který vzdoroval uspokojivému vysvětlení
pomocí vlnové povahy světla, byl fotoelektrický jev zvaný
zkráceně fotoefekt. Tento jev, poprve
pozorovaný již koncem 80.let 19.stol. A.Stoletovem (při
pokusech se zářením elektrického oblouku) a H.Hertzem (při
proslulých jiskrových experimentech prokazujících
elektromagnetické vlny) spočívá v tom, že když na určité
látky, především kovy, dopadá světlo či obecně
elektromagnetické záření dostatečné frekvence, uvolňují
se z jeho povrchu elektrony *).
*) Rozlišujeme dva druhy fotoefektu,
vnější a vnitřní. Zde se zabýváme vnějším
fotoefektem, kdy působením záření se uvolňují
elektrony, jež unikají povrchem z látky do
okolního prostoru - nastává fotoemise elektronů.
Tento jev se využívá ve speciálních elektronkách - fotonkách
a fotonásobičích. Při vnitřním fotoefektu
uvolňované elektrony zůstávají uvnitř ozařovaného
materiálu a přispívají k jeho elektrické vodivosti
(využívá se především u polovodičových optoelektrických
součástek - fotoodpor, fotodioda). V §1.6,
část "Interakce záření
gama a X", obr.1.6.3, se
budeme zabývat speciálním druhem fotoefektu, kdy
vysoenergetická kvanta rentgenového nebo g záření vyrážejí
elektrony z vnitřních slupek atomového obalu a zmíníme též
tzv. jaderný fotoefekt či fotojadernou reakci.
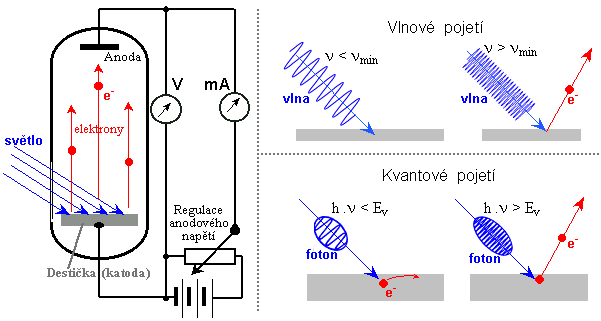
Fotoelektrický jev
Vlevo: Experimentální uspořádání pro studium
fotoefektu. Vpravo nahoře: Ozařování ani
silným dlouhovlnným zářením nevede k fotoefektu, zatímco
ozařování i slabým krátkovlnným zářením fotoefekt
vyvolává.
Vpravo dole: Kvantový mechanismus fotoefektu
absorbcí fotonů dopadajícího záření a předání jejich
energie elektronům.
Podrobnější experimentální sledování
(pomocí elektronové trubice na obrázku vlevo - prototypu tzv. fotonky)
ukázalo, že fotoefekt má určité specifické vlastnosti, z
nichž některé se nedají vysvětlit klasickou vlnovou
představou elektromagnetického záření :
¨ 1. Pro každý kov existuje určitá mezní minimální
frekvence nmin, při níž
dochází k fotoefektu; je-li n<nmin, k fotoefektu
nedochází ani při sebevětší intenzitě záření. Naopak i
slabé záření o vyšší frekvenci vyvolá fotoefekt (i když počet emitovaných elektronů je nižší) a to okamžitě;
podle vlnové představy by elektron musel "čekat",
až mu slabá vlna postupně přinese dostatek energie k
uvolnění. Plyne z toho, že pokud se elektron uvolní, nemůže
dostávat energii postupně a spojitě, ale musí dostat
potřebnou energii naráz.
¨ 2. Počet emitovaných elektronů je přímo úměrný
intenzitě dopadajícího záření (pokud ovšem fotoefekt
nastane).
¨ 3. Kinetická energie (rychlost)
emitovaných elektronů nezávisí na intenzitě dopadajícího
záření. Závisí poněkud na ozařovaném materiálu a je přímo
úměrná frekvenci dopadajícího záření.
Klasická vlnová představa nedokázala
uspokojivě vysvětlit nezávislost energie emitovaných
elektronů na intenzitě dopadajícího záření a naopak její
závislost (dokonce přímou úměrnost) na frekvenci. A.Einstein
v r.1905 podrobně studoval vlastnosti fotoefektu a všechny
experimentálně zjištěné skutečnosti vysvětlil
předpokladem, že pohlcování zářivé energie se děje nikoli
spojitě, ale v určitých malých dávkách, kvantech. Elektromagnetická vlna o
frekvenci n a vlnové délce l = c/n se při fotoefektu chová jako soubor částic
- světelných kvant o určité energii E
a hybnosti p: E = h.n, p = E/c = h.n/c = h/l.
Elektromagnetické záření (včetně světla) se tedy nejenom
vyzařuje, ale i šíří a interaguje (absorbuje) po
jednotlivých kvantech.
Elektron na povrchu destičky přijme právě energii Ef = h.n jednoho světelného
kvanta - fotonu. Část této energie
se spotřebuje na práci potřebnou k uvolnění elektronu z kovu
(výstupní práce rovná vazbové energii Ev elektronu v kovu, která je poměrně malá - jednotky
elektronvoltů). Zbytek se přemění v kinetickou energii Ek = (1/2) mev2 emitovaného elektronu o hmotnosti me, vylétajícího
rychlostí v. Zákon zachování energie pak vede k Einsteinově
fotoelektrické rovnici h.n = Ek + Ev , která kvantitativně popisuje vlastnosti
fotoelektrického jevu v dokonalém souladu s
experimentem. Při větších vlnových délkách, tj.
nižších frekvencích, je energie fotonu nedostatečná k tomu,
aby se elektron uvolnil z vazby v kovu (či v atomu) - k
fotoefektu nedochází.
Comptonův rozptyl
Částicová povaha krátkovlnného
elektromagnetického X a gama záření se nepřímo projevuje v
některých jejich interakcích jako je Comptonův rozptyl
tohoto záření na elektronech. Experiment ukazuje, že čím
vyšší je po rozptylu na elektronu změna směru
elektromagnetického záření, tím nižší je jeho frekvence.
Tuto závislost frekvence na úhlu rozptylu je obtížné
vysvětlit pomocí elektromagnetické interakce rovinné vlny s
elektronem. Zato představa, že k interakci dochází
mechanismem srážky fotonu o energii E=h.n s elektronem,
obdobné pružné srážce dvou těles (jako
jsou "kulečníkové koule"), při nichž se
přerozdělení směrů pohybu, rychlostí a energií (a tím i
vlnových délek a frekvencí) řídí jednoduchými zákony
klasické mechaniky hmotných bodů, velmi dobře vysvětluje
pozorované výsledky Comptonova rozptylu -
je analyzováno v §1.6, část "Interakce záření gama a X", pasáž "Comptonův rozptyl".
Korpuskulárně-vlnový
dualismus elektromagnetického vlnění
je ilustrován na obr.1.1.1. V horní části obrázku je
schématicky znázorněno nejprve běžné elektromagnetické
vlnění o nižší a vyšší frekvenci (tj. větší a menší
vlnové délce). Zvyšujeme-li frekvenci n elektromagnetického
vlnění, podle klasické fyziky se se neděje nic jiného, než
že se úměrně bude zkracovat vlnová délka (l = c/n). Při hodně
vysokých frekvencích (řádově n»1014Hz, tj. l»10-7m) však budeme pozorovat, že vlna nebude již mít
konstantní amplitudu, nýbrž její amplituda bude fluktuovat.
Tato tendence se bude zvětšovat s rostoucí frekvencí a
klesající vlnovou délkou. Při extrémně vysokých
frekvencích n»1018Hz (odpovídajících již záření g) nakonec
zjistíme, že vlna v klasickém smyslu nám zmizela - záření
se bude vyzařovat a šířit v krátkých dávkách -
kvantech (obr.1.1.1 dole) částicového charakteru,
mezi nimiž jsou relativně dlouhé nepravidelné
"mezery".
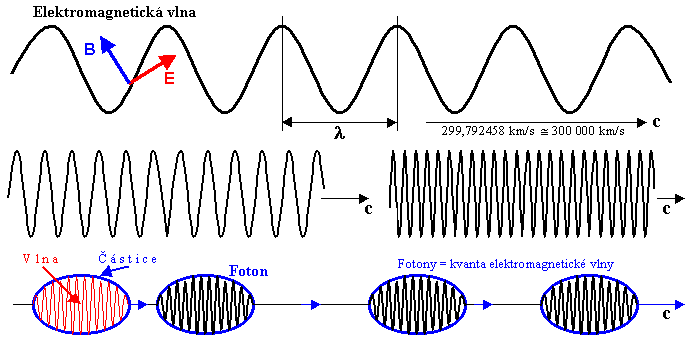
Obr.1.1.1. Schématické znázornění
korpuskulárně-vlnového dualismu u elektromagnetické vlny. V
horní části je znázorněna elektromagnetická vlna o delší
a kratší vlnové délce, v dolní části kvantová představa
šíření záření po kvantech - fotonech.
Kvanta elektromagnetického vlnění se
nazývají fotony (tento název navrhl americký
chemik G.N.Lewis) - můžeme si je
představit jako jakési "balíčky" či
"klubíčka" elektromagnetického vlnění o určité
frekvenci, které se pohybují rychlostí světla c
(dolní část obr.1.1.1). Každý foton obsahuje určité
množství energie E, které je tím větší, čím
větší je kmitočet n: E = h.n, kde h je Planckova konstanta
(h = 6,6251.10-34 J.s). Tato konstanta hraje základní úlohu při
všech jevech v mikrosvětě. V kvantové mechanice se často
používá i "přeškrtnutá" Planckova konstanta h = h/2p. Foton je
základním objektem mikrosvěta, který má částicové i
vlnové vlastnosti, ale striktně vzato není ani částicí ani
vlnou.
Obecně se pozoruje, že v dlouhovlnné oblasti
spektra se více projevují vlnové vlastnosti (ohyb,
interference, rozptyl, lom), zatímco v krátkovlnné části
spektra se více projevují vlastnosti částicové (fotoefekt,
Comptonův rozptyl, tvorba nových částic při interakcích).
Záření gama, i když je to svou podstatou elektromagnetické
vlnění, se bude chovat již jen jako proud částic -
fotonů a žádným makroskopickým experimentem
neprokážeme jeho vlnové vlastnosti; pouze kdybychom se v
myšleném pokuse stali "malými zelenými trpaslíky",
dovedli se zmenšit na rozměry řádově pikometrů a
"vstoupili" dovnitř fotonu, zjistili bychom že foton
je uvnitř vlastně elektromagnetickou vlnou...
Fyzikální procesy
emise Ţ vlnový či fotonový charakter
záření
Vlnový či fotonový charakter elektromagnetického záření
úzce souvisí s mechanismy a s prostorovými a časovými
měřítky fyzikálních procesů, při nichž je toto záření emitováno.
V elektrických obvodech (oscilátorech LC a anténách)
rozměrů milimetry - metry - stovky metrů vznikají
elektromagnetické kmity frekvencí řádově gigahertzů, stovky
MHz či kHz, což vede k vyzařování plynulých
elektromagnetických vln (vlnových délek milimetrů, metrů či
stovek metrů), u nichž se fotonový charakter neprojevuje.
Světlo, vznikající deexcitací vnějších elektronových
slupek atomů o rozměrech ~10-8cm, již nese výrazné stopy kvantového charakteru
přechodů mezi elektronovými hladinami; chová se jako vlnění
i jako proud fotonů. A záření gama,
vznikající při velmi rychlých kvantových deexcitacích v
atomových jádrech velikosti ~10-13cm, již má zcela fotonový charakter.
Detekce nízké
intenzity vysokoenergetického záření Ţ manifestace korpuskulárního charakteru
Jak můžeme nejsnadněji, v běžných
laboratorních podmínkách, prokázat
korpuskulární charakter elektromagnetického záření?
Především, místo obyčejného světla je vhodné použít
vysokoenergetické záření gama a toto
záření registrovat pomocí dostatečně citlivého elektronického
detektoru - G.M. nebo scintilačního (§2.3 "Geiger-Mullerovy
detektory", §2.4 "Scintilační
detektory").
Při měření ve svazku s vysokou intenzitou bude signál na
výstupu detektoru stabilní a kontinuální, v souladu s
představou spojitého pole záření. Při snížení intenzity
záření se začne projevovat kolísání výstupního
signálu - statistické fluktuace (jsou analyzovány v §2.11 "Statistický rozptyl a chyby měření"). Pokud ještě výrazněji
snížíme intenzitu záření, bude detektor registrovat
časově oddělené diskrétní impulsy - odezvy
na průlet jednotlivých částic detektorem.
Další možností je detekce záření pomocí dostatečně
citlivé fotografické emulze (§2.2 "Fotografická detekce ionizujícího
záření").
Při vysoké intenzitě záření bude film po vyvolání
kontinuálně zčernalý podle míry celkové expozice. Nízká
intenzita záření však nevyvolá v objemu fotografické emulze
spojitě rozloženou odezvu, ale budou vidět jednotlivé oddělené
stopy, jako kdyby je zanechaly prolétající
částice...
Vlnové
vlastnosti částic
Vidíme tedy, že elektromagnetické vlny se mohou chovat jako
proud částic - toto je jedna stránka korpuskulárně-vlnového
dualismu. Jak je to však s chováním (skutečných) částic?
Podle klasické fyziky se částice za všech okolností chovají
jako diskrétní "kousíčky hmoty". Pokusy s
průchodem elektronů, což jsou typické částice v atomové
fyzice, přes jemné mřížky *) však ukázaly, že elektrony
vykazovaly ohyb a interferenci podobně jako
vlny - jako kdyby se elektron "rozdvojil", prošel
současně dvěma sousedními otvory mřížky a pak po ohybu
tyto dvě složky spolu interferovaly jak je to běžné u
vlnění. Ohybové interferenční jevy byly pozorovány i u
dalších druhů částic (korpuskulárního záření). Přitom
tyto interferenční jevy nezávisejí na intenzitě toku
částic - obrazec se nemění, i když intenzita toku elektronů
je tak malá, že systémem prochází jeden elektron po druhém!
*) Davisson-Germerův
experiment
Vhodnou strukturou pro uskutečnění difrakčních a
interferenčních pokusů v mikrosvětě je krystalová
mřížka, jejímiž uzly jsou jednotlivé atomy
krystalu s typickými vzájemnými vzdálenostmi cca 10-7cm. Takováto
difrakční měření s elektrony poprvé prováděli
C.J.Davisson, L.H.Germer a J.J.Thomson v r.1927. Svazek
elektronů urychlených napětím U»50V pouštěli na povrch
krystalu niklu. Elektrony odražené od povrchové vrstvy atomů
krystalu registrovali pomocí detektoru, který byl nastavitelný
pod různými úhly ("goniometr"). Bylo pozorováno,
že elektrony se nerozptylují do všech směrů přibližně
rovnoměrně, ale do některých směrů se jich rozptylovalo
výrazně víc, do jiných směrů se jich rozptylovalo
podstatně méně, v rozptylovém obrazci se střídala minima a
maxima rozptýlených elektronů. Při měření závislosti
intenzity rozptýlených elektronů na směru rozptylu pozorovali
zřetelná minima a maxima, odpovídající Braggově
podmínce interference, stejné jako je při difrakci
X-záření na krystalové mřížce - aby dráhový úhel dvou
paprsků byl celočíselným násobkem vlnové délky l: n.l = 2.d.sinJ; n=1,2,3,..(řád
interferenčního maxima), d je vzdálenost mezi dvěma
sousedními uzly krystalu (mřížková konstanta), J je úhel rozptylu.
Vlnové záření rozptýlené na jednotlivých atomech
krystalové mřížky se interferencí zesílí ve směrech, ve
kterých je dráhový rozdíl vln rozptýlených na jednotlivých
atomech roven celočíselnému násobku vlnové délky. A stejně
tak se chovaly elektrony, pro něž vycházela "vlnová
délka" l » h/Ö(2me.e.U), což odpovídá tzv. Broglieově vlnové
délce (urychlovací napětí U dodá elektronům
o náboji e a hmotnosti me kinetickou energii Ek= e.U a hybnost p=Ö[2me.e.U], takže l=h/p).
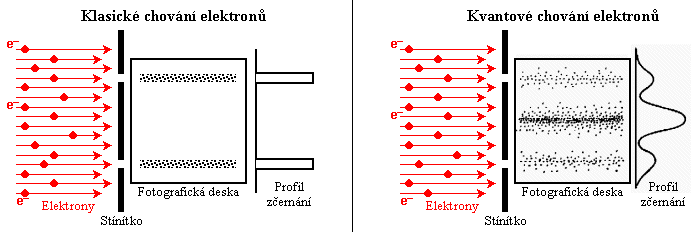
Obr.1.1.2. Vlnové vlastnosti částic se
projevují v myšlenkovém experimentu difrakce elektronů na
štěrbině vznikem interferenčních obrazců.
Podstata těchto experimentálních
skutečností je názorně ilustrována na obr.1.1.2 v myšleném
experimentu, který zobecňuje výsledky mnoha skutečných
experimentů. Svazek rovnoběžně letících elektronů dopadá
na neprostupné stínítko s dvěma štěrbinami, za nímž je
umístěna fotografická deska. Pokud by elektrony byly klasické
částice s přímočarým šířením, na fotografické desce by
po vyvolání byly zobrazeny dva tmavé pruhy jakožto stínové
obrazy obou štěrbin (obr.1.1.2 vlevo). Ve skutečnosti však
obdržíme interferenční obraz - střídání
světlých a tmavších proužků (obr.1.1.1 vpravo), přesně
takový, jaký by vznikl při průchodu rovinné vlny
s vlnovou délkou l = h/p, kde p=me.v je hybnost elektronu. Interferenční obraz
nezávisí na intenzitě dopadajícího svazku, takže není
důsledkem vzájemné interakce elektronů ve svazku. Kdybychom
zeslabili tok elektronů natolik, že by se v soustavě při
každém průchodu nacházel vždy jen jeden elektron, každý
takový prošlý elektron by vytvořil na desce své lokální
("bodové") zčernání. Výsledný obraz, který je
součtem skvrnek způsobených jednotlivými elektrony, by
přesto měl charakter podle obr.1.1.2 vpravo. Jev tedy nastává
i tehdy, když na stínítko dopadají jednotlivé elektrony
postupně za sebou: jakoby jednotlivý elektron prošel oběma
otvory stínítka současně - jako kdyby s každým jednotlivým
elektronem byla spojena vlna, která po průchodu oběma otvory
interferuje. K tomuto experimentu se krátce vrátíme níže v
odstavci o kvantové mechanice, pro jejíž
podstatu má klíčový význam.
Rozbor těchto experimentů (skutečných i myšlených) vedl
k závěru, že každá mikročástice o hmotnosti m
pohybující se rychlostí v, se může chovat jako vlna
o vlnové délce l = h/m.v = h/p, kde p je hybnost částice (tato vlnová délka se někdy nazývá Broglieova-Comptonova
vlnová délka). A to je druhá
stránka korpuskulárně-vlnového dualismu. Získané poznatky
můžeme celkově shrnout následujícím způsobem:
| Korpuskulárně-vlnový dualismus |
Vlnění
o frekvenci n se může chovat jako
proud částic (kvant - fotonů) o energii E = h.n . |
Brána k pochopení
kvantové fyziky
Dualita mezi vlnami a částicemi je "bránou"
k pochopení kvantové fyziky! Pokud to
někteří současní kvantoví fyzikové zpochybňují, jedná
se o nedorozumění v duchu přísloví "Po bitvě je
každý generálem". Nebýt prozkoumání
korpuskulárně-vlnového dualismu, řada novějších koncepcí
kvantové fyziky by nevznikla, nebo by vznikly mnohem později a
byly by obtížně pochopitelné. Téměř všechny jevy v
mikrosvětě se pomocí tohoto dualismu dají názorně
vysvětlit. Částicově-vlnový dualismus podstatně
zmírňuje onu nepříjemnou "nepochopitelnou-nepochopitelnost"
kvantové fyziky, diskutovanou níže v pasáži "Interpretace
kvantové fyziky".
Kvantová
povaha mikrosvěta
Klasická mechanika, rozšířená a zobecněná
Einsteinovou speciální teorií relativity, spolu s klasickou
Maxwellovou elektrodynamikou, dokáže vysvětlit téměř
všechny jevy pozorované v makrosvětě našich
zkušeností. Klasická fyzika (především Newtonovská
mechanika) je zobecněním naší každodenní zkušenosti, podle
níž hmotné ojekty existují nezávisle na pozorovateli, mají
určité polohy a rychlosti, pohybují se po přesně vymezených
drahách.
Jak jsme však poznali v odstavci o korpuskulárně-vlnovém
dualismu a jak ještě více poznáme v dalších
kapitolách o atomech, atomových jádrech,
jaderných reakcích, radioaktivitě, elementárních
částicích a jejich interakcích, čím hlouběji
jdeme do mikrosvěta stavby hmoty, tím více se
experimentální chování mikrosystémů liší od zákonitostí
klasické fyziky. Pro pochopení a popis atomárních a
subatomárních procesů, které se odehrávají ve velmi malých
částech prostoru a kterých se účastní částice s velmi
malými hmotnostmi, bylo potřeba principiálně změnit či
doplnit základní klasické představy a zákony - vybudovat
novou fyziku mikrosvěta, kvantovou fyziku.
Pozn.: Tuto "novou fyziku" si
nelze představit tak, že by snad vyvracela a bořila
"starou" klasickou (nekvantovou) fyziku. V
přírodovědě (a ve fyzice zvlášť) platí kontinuita
vědeckého poznání. Kvantová fyzika nevyvrací,
nýbrž doplňuje, upřesňuje a zobecňuje klasickou fyziku na
jevy, které již není schopna vysvětlit; přitom obsahuje
klasickou fyziku jako limitní případ. Vztah
mezi klasickou a kvantovou fyzikou se formuluje jako tzv. princip
korespondence: V limitě velkých kvantových čísel se
stírá rozdíl mezi kvantovou a klasickou fyzikou, kvantová
fyzika přechází v klasickou. Neboli pro velká kvantová
čísla dává kvantová fyzika stejné výsledky jako fyzika
klasická (bude ukázáno níže). I když se tedy atomy a
subatomární částice, z nichž je všechno složeno, řídí
kvantovou fyzikou, jejich velké soubory, jež tvoří
makroskopická tělesa (včetně nás) se s velkou přesností
řídí klasickou Newtonovou mechanikou. Čím je objekt
větší, tím méně zřetelně se projevuje jeho kvantová
povaha.
Ve fenomenologické fyzice
makrosvěta jsou částice ze kterých je vnitřně všechno
složeno, jako jsou atomy, elektrony, protony, fotony, ...,
považovány za tvrdá a pevná "tělíska" či hmotné
body, pohybující se podle zákonů mechaniky a elektrodynamiky.
Jejich soubory se řídí zákony termodynamiky, mechaniky a
elektrodynamiky kontinua. V koncepci teorie pole se navíc
částice snažíme interpretovat jako "kondenzované
zhuštěniny" fyzikálních polí.
V kvantové mechanice však již
částice není žádným pevným a tvrdým tělískem či
přesným bodem, ale jen oblakem rozmazané pravděpodobnosti,
popisující kde bychom částici mohli najít při měření či
detekci. Tyto rozmazané pravděpodobnosti se modelují jako kvantové
stavy a vlnové funkce (je
podrobněji diskutováno níže).
Náhodnost a pravděpodobnost v kvantové
fyzice
Jak již bylo zmíněno výše (pasáž
"Klasické a kvantové modely v mikrosvětě"), základním specifickým rysem mikrosvěta je stochastický
(pravděpodobnostní) charakter kvantových jevů. Pohyb částic
a všechny ostatní jevy v mikrosvětě vykazují kvantové
fluktuace - chaotické kolísání poloh částic a
jejich rychlostí, intenzit polí, hodnot energie a dalších
veličin. Tyto fyzikální veličiny kolísají kolem svých
středních hodnot; velikost kvantových fluktuací je omezena
tzv. relacemi neurčitosti, zmíněnými níže. Při
kvantových fluktuacích může být na kratičký okamžik porušen,
či lépe řečeno přerušen, klasický zákon
zachování energie a hybnosti, jakož i další klasické
zákonitosti přesně platící v klasické fyzice.
Kvantová fyzika není
schopna s jistotou předpovědět konkrétní výsledky
měření. Nabízí jen jednotlivé alternativy hodnot a jejich pravděpodobnosti.
A stav studovaného systému se po změření změní.
Podle kvantové fyziky výsledek nějakého
fyzikálního procesu v daném systému nelze přesně a
jednoznačně předpovědět - bez ohledu na to, jak přesně
známe počáteční stav systému a jak přesně dokážeme
řešit příslušné rovnice dynamiky systému. Vývoj systému,
stejně jako výsledek experimentu, nelze určit jednoznačně,
existuje jen řada různých možných výsledků, z nichž
každý má určitou pravděpodobnost *). Když
mnohokrát zopakujeme určitý experiment, frekvence různých
výsledků odpovídá pravděpodobnostem předpovězeným
kvantovou fyzikou.
*) A.Einstein to metaforicky připodobnil k
situaci, jako kdyby Bůh pokaždé hodil hrací kostkou a až
podle výsledku který padne rozhodl, jak experiment dopadne. S
touto představou se Einstein nikdy nesmířil...
Kvantová teorie tak ukazuje na novou
formu determinismu na hlubší mikroskopické úrovni:
známe-li stav systému v daném okamžiku, fyzikální zákony
neurčují jednoznačně budoucnost (příp. rekonstruovanou
minulost), ale určují jen pravděpodobnosti různých
budoucností (nebo minulostí).
Střílení ze vzduchovky
Pravděpodobnosti a náhodnosti vyskytující se v běžném
životě jsou odrazem nepřesností ve znalosti počátečních
podmínek a dalších, často složitých, vlivů. Když
střílíme vzduchovkou na terč, broky s různou
pravděpodobností zasáhnou různá místa terče v okolí
středu, podle obratnosti střelce. Tato pravděpodobnost není
vlastností pohybu broků směrem k terči, ale je způsobena
neznalostí a variabilností okolností střelby. Kdybychom
vzduchovku upevnili do svěráku, dopadaly by broky do jednoho
přesně zaměřeného místa. Pravděpodobnosti v kvantové
fyzice však vyjadřují principiální náhodnost,
která je vlastní samotné podstatě jevů.
Mikročástice zaměřené a vysílané za stejných
počátečních podmínek budou dopadat pokaždé do poněkud
jiného místa v okolí středu terče.
Na zdánlivě triviální
otázku "Kde se něco nachází?" odpovídá klasická
přírodověda tak, že "Každá věc je na jednom
konkrétním místě", jak ukazuje běžná naše
zkušenost, zachycená v klasické fyzice spočívající na
Newtonových základech. V mikrosvětě se ukazuje, že je tomu
jinak: subatomární částice mohou být na několika místech
"současně". Jejich přesné souřadnice podléhají
kvantovým relacím neurčitosti (fluktuují) a své konkrétní
hodnoty získávají až v momentu, kdy je začneme měřit (v
okamžiku interakce). Jako by něco začalo existovat až v
momentu, kdy na to "podíváme" (tato
zavádějíví interpretace je diskutována níže v pasáži
"Pozorování a měření v
mikrosvětě")...
Je kvantová
stochastičnost principiální, nebo je způsobena skrytými
neznámými parametry? Lokální realismus?
Každý, kdo se začíná seznamovat s kvantovou mechanikou, je
při hlubším zamyšlení zaskočen určitou "nepatřičností"
chování částic a sytémů, neintuitivností, v rozporu se
zdravým rozumem a přírodní zkušeností. Je toto překvapivé
a nepochopitelné chování opravdu fundamentální,
nebo za ním stojí nějaké další, skryté a nám zatím
neznámé vlivy - skryté parametry? V takovém
případě by standardní kvantová fyzika byla neúplnou
teorií a její stochastický charakter by byl důsledkem neznalosti
nějakých skrytých (nám zatím nedostupných) parametrů,
které nabývají různých hodnot. Chování těchto parametrů
by mělo být popsatelné nějakou budoucí "fundamentálnější"
teorií, patrně v rámci unitární "teorie všeho".
A.Einstein, ač významně přispěl ke vzniku
kvantové fyziky, se s některými jejími budoucími koncepcemi
nikdy nesmířil. Především mu vadila principiální
stochastičnost, naopak věřil že "Bůh se světem nehraje
v kostky!". Dále to byla koncepce nelokální vlnové
funkce, která pro danou částici existuje v celém prostoru a
při interakci naráz - okamžitě - "zkolabuje" v
celém prostoru. Obě tyto námitky, či požadavky, vůči
kvantové fyzice se někdy shrnují pod souhrnnější název lokální
realismus :
1. Princip
lokality :
Příčina fyzické změny objektu-systému musí být lokální:
nastane pouze tehdy, když se ho "dotkneme" - budeme s
ním interagovat silami, poli, na tom místě kde se nachází.
Síla, fyzikální pole, způsobuje účinek tím, že cestuje
prostoročasem a když k objektu doputuje tak s ním interaguje.
Žádné přímé působení na dálku!
2. Princip
objektivni reality :
Vlastnosti objektů jsou skutečné - objektivní,
existují ve fyzikálním vesmíru nezávisle na tom zda je
pozorujeme nebo měříme. A samozřejmě jsou nezávislé na
naší mysli a našem pohledu na přírodní dění.
Tyto principy a jejich splnění či porušení v
kvantové fyzice budou disktovány na několika místech této
kapitoly, v souvislosti s konkrétními jevy a jejich
interpretacemi.
Vraťme se na chvíli k shora zmíněnému
jednoduchému příkladu střílení ze vzduchovky. Pokud bychom
stříleli na volném prostranství na terč vzdálený cca 50
metrů, pozorovali bychom poměrně velký rozptyl zásahů.
Kdybychom neznali či neuvědomili si proměnlivou rychlost a
směr větru, drobné odchylky ve velikosti a tvaru broků a
další možné vlivy, mohli bychom si v zásadě empiricky
vybudovat jakousi "kvantovou mechaniku pohybu broků",
která by ukazovala principiálně stochastický charakter
trajektorie broků..?..
V kvantové mechanice částic mikrosvěta se
žádné takové dodatečné skryté parametry nenašly.
Systémovou analýzou možnosti ovlivnění měřitelných
veličin v kvantové mechanice skrytými parametry se v r.1964
zabýval J.Bell, který stanovil omezující nerovnosti
pro výsledky měření polarizace dvou fotonů z kvantově
"propleteného" páru. Experimentální měření byly
v 80.letech prováděny na fotonových párech při kaskádních
přechodech v atomech vápníku s korelovanými polarizacemi.
Výsledky experimentů poněkud překračovaly hodnoty ±2 v
Bellových nerovnostech. Novější měření, s použitím
....., poskytly hodnotu .... Tyto výsledky jsou považovány za
pádnou indicii proti koncepci skrytých
parametrů a lokálního realismu; otázkou jsou ale různé možnosti
interpretace těchto experimentálních výsledků...
Nynější kvantová fyzika se obecně přiklání
k názoru, že kvantový stav představuje úplný popis
systémů a kvantová stochastičnost a relace neurčitosti mají
fundamentální charakter, který nelze z ničeho
odvodit..?.. Zdá se tedy, že náhodnost je
určitým způsobem zakomponována do nejhlubší podstaty
našeho světa ?
Další neobvyklé jevy
související s kvantovým provázáním jsou
diskutovány níže v pasáži "Kvantová provázanost a teleportace. Kvantové
počítače.".
Statistické fluktuace a
šumy při zobrazování
Emise kvant záření, stejně jako jeho interakce s
atomy látkového prostředí (a tím i mechanismy detekce
záření) probíhá na mikroskopické úrovni
prostřednictvím dějů řídících se nikoli
deterministickými zákony klasické fyziky, nýbrž
zákonitostmi kvantové mechaniky. Tyto
kvantové zákonitosti jsou principiálně stochastické,
pravděpodobnostní. Přechody elektronů v atomech či přeměna
radioaktivních atomů je proto do značné míry náhodný
proces a vznikající záření je emitováno náhodně,
nekorelovaně, inkoherentně *). Tok záření proto není
plynulý, ale fluktuující. Stejně
fluktuující (kolísavá) bude i odezva
každého přístroje detekujícího a zobrazujícího toto
záření - jedná se o fluktuace neodstranitelné
žádným zdokonalením přístroje či metody, tyto fluktuace
mají svůj původ v samotné podstatě
měřených jevů.
*) To, že LASER vyzařuje koherentní
fotony je způsobeno skutečností, že se jedná nikoli o
spontánní, ale stimulovanou produkci fotonů.
Statistické fluktuace (šumy) v měřeních a
obrazech jsou tedy obecným jevem. Skrytě se
projevují i u běžného světla při optickém vidění a
fotografování, kde je ale nepozorujeme vzhledem k velkému
počtu fotonů (řádově 109), které jsou zde k dispozici. V horní části
obrázku je fotografický portrét exponovaný s různým počtem
fotonů světla. Vidíme, že pokud je obraz tvořen méně než
103
fotony, nerozeznáme na obraze vůbec nic kromě rozházených
shluků teček. S rostoucím počtem fotonů se kvalita snímku
zlepšuje (nad 104 fotonů začneme poznávat základní motiv) a při cca
108
fotonech již dostáváme obvyklý fotografický obraz se všemi
detaily, bez patrných šumů.

Vliv registrovaného počtu fotonů na kvalitu obrazu z hlediska
statistických fluktuací (šumu) - kvalita snímků se zlepšuje
s rostoucím počtem fotonů.
Nahoře: Fotografický
portrét exponovaný s různým počtem fotonů světla (počítačové zpracování obrázků provedl
Ing.J.Juryšek).
Dole: Gamagrafický obraz
fantomu (Jasczak, naplněný
radionuklidem 99mTc) nastřádaný scintilační
kamerou s různým počtem fotonů g v obraze.
V praxi se statistické fluktuace
nepříznivě uplatňují všude tam, kde nemáme k dispozici
dostatek kvant (fotonů) zobrazujícího záření. Je to
především při radiačních detekčních, spektrometrických a
zobrazovacích měřeních. Vliv statistických fluktuací na
výsledky těchto měření můžeme zjednodušeně (avšak
výstižně) vyjádřit následujícím pravidlem: Naměříme-li
na radiačním detekčním přístroji N impulsů, naměřili jsme ve
skutečnosti N ± Ö(N) impulsů. Tyto statistické fluktuace se projevují ve
všech buňkách obrazu a jedinou možností jejich snížení je
zvýšit nastřádaný počet impulsů - počet
"užitečných" fotonů g, z nichž vznikne odezva v
obraze. Obraz je ostrý a jasný, pokud je vytvořen alespoň 1
milionem fotonů/cm2. To bývá při gamagrafických zobrazeních obtížně
dosažitelné, v praxi se musíme spokojit často s cca 500-1000
fotony/cm2.
Proto bývají scintigrafické obrazy značně
"zašuměny".
Statistické fluktuace zhoršují kvalitu obrazu
především tím, že se v nich mohou ztratit
užitečné strukturní detaily. Je to vidět v dolní
části obrázku na obrazech fantomu modelujícího
"studené" léze různé velikosti v roztoku g-radionuklidu 99mTc. Pokud je obraz
tvořen méně než asi 104 fotony g, není vidět žádná struktura, jen statistické
fluktuace. Při větším počtu registrovaných fotonů g cca 105 jsou vidět větší
léze a teprve při 107-8 fotonech se zobrazují i nejjemnější struktury s
malými lézemi.
Vedle gamagrafických zobrazení se statistické fluktuace
projevují i u astronomických zobrazení
vzdálených objektů, z nichž k nám dopadá jen velmi málo
světla.
Podstata a interpretace
kvantové fyziky
Systematický výklad kvantové fyziky je mimo tématický rámec
tohoto pojednání *)
a zabral by též enormně mnoho místa (lze
odkázat na standardní učebnice a monografie, např. Landau,
Lifšic: Kvantová mechanika). Uděláme si
zde pouze letmou exkurzi do představ a zákonitostí kvantové
fyziky, abychom si nastínili některé základní
společné principy uplatňující se rozhodujícím
způsobem při procesech s atomy, atomovými jádry a
elementárními částicemi.
*) Ostatně, plně pochopit podstatu
kvantových zákonitostí a vnitřně se s nimi
ztotožnit, není nikterak snadné - ne li nemožné!
Říká se, že teorie relativity je "pochopitelně -
nepochopitelná", avšak kvantová fyzika je
"nepochopitelně - nepochopitelná"..!.. I nejlepší
profesionální specialisté na kvantovou fyziku (včetně jejích budovatelů jako byli Bohr,
Schrodinger, Pauli, Feynman, Fermi, Dirac, Heisenberg, ......) přiznávají, že sice dovedou velmi přesně
analyzovat výsledky kvantových procesů v atomech, jádrech či
interakcích částic, avšak když se jich někdo zeptá, proč
se to tak chová, nevědí...
Kvantová fyzika v
mikrosvětě - ale i v makrosvětě ?
Kvantová fyzika vznikla při studiu jevů v mikrosvětě - na
úrovni atomů, atomových jader, elementárních částic. A tam
má též své hlavní uplatnění.... Kvantová mechanika si
však činí nároky na univerzální platnost
nejen v mikrosvětě, ale i v makrosvětě (dokonce
v megasvětě, viz např. §5.5 "Mikrofyzika
a kosmologie. Inflační vesmír." v knize "Gravitace, černé díry a fyzika
prostoročasu"). Obvyklá představa
je, že uplatnění kvantové fyziky je dáno velikostí
zkoumaných objektů: malé objekty se chovají
kvantově, velké objekty klasicky. Ve skutečnosti to však
takto vždy nemusí být. To, co dělá objekt kvantovým nebo
klasickým, není ani tak geometrická velikost, ale počet
stupňů volnosti, kterým objekt disponuje. Při malém
počtu stupňů volnosti se objekt chová kvantově. Malé
objekty, jako jsou elementární částice (s
jednoduchou strukturou nebo bez struktury),
mají malý počet stupňů volnosti a chovají se jednozmačně
kvantově. Větší objekty, složené z velkého počtu
částic, mají velký počet stupňů volnosti a chovají se
klasicky, protože hodnoty jejich stavových veličin jsou
zprůměrovány přes mnoho stupňů volnosti.
Za určitých okolností mohou mít malý počet
stupňú volnosti i relativně velké makroskopické objekty,
jako je laserový paprsek koherentních fotonů, laboratoní
nádobka se supratekutým héliem, nebo proud Cooperových párů
elektronů v supravodivém drátu. Extrémním případem
dlouhodosahového kvantového chování mohou být stavy
provázaných částic (viz níže "Kvantová provázanost a teleportace. Kvantové
počítače.").
Specifická situace je u kvantových procesů s účastí černých
děr (je podrobně diskutováno v
§4.7 "Kvantové vyzařování a termodynamika
černých děr"
zmíněné monografie).
Pro běžná tělesa makroskopických hmotností a
rozměrů jsou kvantové efekty zcela nepatrné a neměřitelné.
V pokročilých citlivých experimentech se však daří
pozorovat kvantové vlastnosti u stále větších objektů (jako
jsou makromolekuly)...
Vlnový stochastický popis
částic a systémů. Interpretace kvantové fyziky.
V klasické (nekvantové) fyzice se stav fyzikálního systému
popisuje pomocí přímo meřitelných veličin, jako jsou polohy
a hybnosti částic. V kvantové fyzice je stav částic
popisován vlnovou funkcí (viz
níže), jejíž druhá mocnina udává pravděpodobnost,
že se částice nachází v konkrétním stavu. Vlnová funkce
není přímo meřitelnou fyzikální veličinou, ale spíše
modelovou představou. Při interakci částice s jinou
částicí dochází k dekoherenci (ztrátě
vzájemné prostorové a časové souvislosti fáze a amplitudy) vlnové funkce, vedoucí k tomu, že částice nabudou
konkrétní měřitelný stav jako v klasické fyzice. Jedná se
zde však pouze o pravděpodobnost, že v nějakém
místě a čase naměříme určitou hodnotu stavové veličiny.
Nedá se dopředu předpovědět, jaká hodnota se v konkrétním
případě naměří, lze jen stanovit pravděpodobnostní
rozdělení výskytu různých naměřených hodnot při větším
počtu měření (za stejných podmínek).
Z gnoseologického hlediska je ale třeba mít
neustále na paměti, že toto všechno jsou jen matematické modely,
umožňující popis a kvantifikaci jevů v
mikrosvětě. Jejich fyzikální podstata je asi
skryta někde hlouběji..?..
Souběžně s budováním vlastní kvantové
mechaniky a jejího matematického formalismu se vytvořilo i
několik způsobů interpretace kvantových
zákonitostí a heuristických postupů tvorby řetězce pojmové
struktury kvantové fyziky. My se zde většinou přidržíme induktivního
postupu vycházejícího z postupného rozboru experimentálně
zjištěných skutečností (budeme ji
pojímat fyzikálně, bez diskutabilních filosofických
spekulací). Nejčastější přístup je
tzv. Copenhagen - Kodaňská interpretace
kvantové mechaniky, založená fyzikální skupinou pod vedením
Nielse Bohra. Podle ní při měření či interakci
dochází ke "kolapsu"
vlnové funkce *) (popisující
původně superpozici možných stavů) - k
redukci kvantových alternativ. To donutí částici
pravděpodobnostně "vybrat" si pouze jeden výsledný
stav a polohu (která byla do té doby
neurčitá), tak jak je to v klasické
fyzice. Při tomto kolapsu se nezachovává původní informace,
kterou již nelze nijak zjistit - částici od okamžiku
měření či interakce popisuje úplně nová vlnová funkce.
*) "Kolaps vlnové funkce"
je jen modelovou matematickou abstrakcí, není to
reálný fyzikální proces! Kdybychom brali vážně
kolaps vlnové funkce naráz v celém prostoru, v podstatě by to
znamenalo, že "zahodíme" jeden vesmír a nahradíme
ho jiným vesmírem s novou vlnovou funkcí. Taková představa
by se již blížila mnoho-vesmírové Everettově hypotéze. K
ničemu takovému samozřejmě ve skutečnosti nedochází.
A není nutný žádný antropomorfní
"vědomý" pozorovatel; procesy interakcí probíhají
v nesčíselném množství spontánně v neživé i živé
přírodě. Naše "pozorování" jsou jen vzácnými
nahodilými "sondami" do těchto procesů.
V pasáži "Mystická kvantová fyzika?" zmíníme poněkud bizarní mnoho-vesmírovou
interpretaci H.Everetta, podle které při měření či
interakci nenastává kolaps vlnové funkce, ale vytvoří se paralelní
reality ("vesmíry"), ve kterých existují
všechny možné stavy výsledných částic; avšak tyto
částice již pak spolu nemohou nijak interagovat. V závěru
této obecné části se pak stručně zmíníme o Feynmanově
přístupu kvantování "dráhových integrálů", který dává určitou možnost pochopit vnitřní
příčiny kvantového chování.
Superpozice různých stavů a
kolaps vlnové funkce: někdy chybná interpretace kvantové
fyziky ?
Pojetí "kolapsu vlnové funkce" popisující
superpozici různých možných stavů je však jen teoretický
model, který může být zavádějící. Ukazuje to
např. jednoduchý (Stern-Gerlachův) experiment, při němž neutrální atomy, vypařované
ve vhodnéhom zdroji, urychlíme a necháme je procházet přes
nehomogenní magnetické pole tvořené dvěma pólovými
nástavci umístěnými nad sebou. Po průchodu budou dopadat na
detekční destičku. Atomy s různými spinovými stavy se budou
v mag. poli chovat odlišně. Podle polarity magnetického pole
atomy se spinem +1/2 budou vychylovány nahoru, atomy se spinem
-1/2 se budou vychylovat dolů. Za normálních podmínek
pravděpodobnost, že neutrální atomy mají spin +1/2 nebo
-1/2, je 50%/50%, takže bude detekováno stejné množství
částic, které se vychýlily nahoru i dolů. Víme pak s
jistotou, že atomy pohlcené na horní straně mají spin +1/2 a
pohlcené na dolní straně spin -1/2. Nedošlo zde k žádnému
"kolapsu vlnové funkce", jen před měřením
jsme neznali konkrétní spinový stav částic, pouze jsme
věděli že může být +1/2 nebo -1/2. Po měření známe
spinový stav detekovaných částic - které byly s tímto
stavem již na počátku ze zdroje emitovány.
Částice není před
pozorováním-měřením ve všech možných stavech najednou -
je jen v jednom stavu, který neznáme. My před
měřením můžeme stanovit pouze pravděpodobnost, v
jakém stavu by mohla být. A po měření pak známe konkrétní
stav jistě. Často se vyskytující chybnou
interpretaci kvantové mechaniky si ještě prodiskutujeme níže
v pasáži "Schrodingerova kočka".
Vlnová
funkce
Vraťme se ke korpuskulárně-vlnovému dualismu (obr.1.1.1 a
1.1.2), který je důležitou charakteristickou vlastností kvantového
chápání mikrosvěta - naznačuje, že rozdělení
hmoty na vlny a částice je pouze formální; obecně musíme
korpuskulární i vlnové vlastnosti uvažovat současně.
Částice se nepohybuje po nějaké pevné lokalizované dráze,
ale jako by se "vlnila" po rozmazané dráze,
chová se jako Broglieova vlna.
Jaký je fyzikální význam Broglieho vln
spojených s pohybem částic? První přímočará představa,
že částice samotné jsou vlnové útvary, neobstojí, neboť
bychom při některých procesech, především při rozptylu,
mohli v principu registrovat "části vln" jakožto
"fragmenty" částice, v rozporu s experimenty. Ani
opačná představa, že vlny jsou útvary složené z částic,
nevyhovuje (žádné částice
pocházející z vlny nebyly pozorovány, pouze vlna se při
interakci může chovat jako kvantum s vlastnostmi částice). Adekvátnější představu o vztahu vln a pohybu
částic můžeme získat studiem difrakce elektronů, které
registrujeme na fotografickém filmu (obr.1.1.2). Projde-li jen
malý počet elektronů, dostaneme na filmu rozházený
nepravidelný obraz, avšak po průchodu velkého počtu
elektronů dostáváme hladký pravidelný obrazec analogický
difrakčním obrazům světelných vln. Tato skutečnost
přivádí ke statistické interpretaci
Broglieových vln: že totiž intenzita Broglieových vln v
libovolném místě prostoru je úměrná pravděpodobnosti
výskytu částice v daném místě. Klasická dráha
částice je nahrazena jakýmsi "pravděpodobnostním
oblakem", představujícím množinu míst, v nichž se
částice vyskytuje s různými pravděpodobnostmi.
V kvantové mechanice je stav částice (resp. souboru
částic a obecně každého fyzikálního systému) popsán tzv.
vlnovou funkcí y(x,y,z) (v nejjednodušším případě izolované částice je
tato vlnová funkce totožná s Broglieho vlnou). Fyzikální význam vlnové funkce je ten, že druhá
mocnina modulu vlnové funkce úyú2 určuje pravděpodobnost
dW, že se částice v daném čase t nalézá v elementu
objemu dV = dx.dy.dz kolem bodu (x,y,z): dW = úyú2.dx.dy.dz. A střední hodnota libovolné fyzikální
veličiny F(x,y,z), jež je funkcí souřadnic x,y,z, je pak
dána vztahem`F(x,y,z) = ňF(x,y,z).úyú2.dx.dy.dz, kde se
integruje přes celý obor proměnných x,y,z.
Pozn.: Vlnová
funkce y
se obecně zavádí jako komplexní funkce
(obsahující reálnou i imaginární složku), takže čtverec
modulu úyú2 = y.y*, kde y* je komplexně
sdružená funkce k y. Pro nejjdnodušší případ volné částice
pohybující se ve směru osy x s hybností px se vlnová funkce
píše ve tvaru y = exp[- i/h (E.t - px.x)],
představujícím rovinnou harmonickou vlnu.
Pozorování a měření v
mikrosvětě
"Věci lze
pozorovat, aniž je porušíme"
- to je zkušenost z běžného života, zvláště z
vizuálního pozorování "nezúčastněným
pozorovatelem". Proces pozorování
či měření *) v mikrosvětě se však svým
charakterem a svými důsledky diametrálně liší od procesů
měření a pozorování v klasické fyzice popisující
makrosvět.
*) Výrazy "pozorování" a
"měření" se často nerozlišují: kvantitativní
pozorování je měřením.
Ve fyzice klasických systémů
makrosvěta se mlčky předpokládá, že proces pozorování
(měření) nenaruší podstatně jejich pohyb
či evoluci. Příslušné fyzikální veličiny mohou být
dostatečně přesně změřeny bez toho, že by se narušily
jejich hodnoty nebo že by se narušil vývoj pozorovaného
systému. Popř. předpokládáme, že jakákoli porucha
vyvolaná měřením může být přesně zkorigována,
aspoň v principu.
Např. při měření napětí v elektrickém obvodu
použijeme buď voltmetr s dostatečně velkým vstupním
odporem, který měřenou hodnotu prakticky neovlivní, nebo
když to nejde, můžeme při znalosti impedancí v obvodu a ve
voltmetru provést přesnou korekci změny napětí. Zkušení
elektronikové však vědí, že při měření extrémně
slabých elektrických signálů (jichž se účastní třebas
jen několik stovek elektronů) se uplatňují neodstranitelné
šumy a fluktuace, přičemž všechny korekční metody zde již
selhávají.
Nejobvyklejší způsob, jak zkoumat polohu
nějakého objektu, je jeho vizuální pozorování:
ozáříme pozorovaný předmět světlem (pokud
sám není zdrojem světla) a naše oči
registrují odražené fotony světla. Pokud má pozorované
těleso makroskopickou velikost a hmotnost (třebas
jablko nebo kámen), dopadající a
odražené fotony světla nijak znatelně neovlivní polohu
tělesa a základní předpoklad "nezúčastněného
pozorovatele" je splněn. Je-li však těleso
mikroskopických rozměrů a hmotnosti, náraz každého fotonu
může znatelně ovlivnit jeho polohu a rychlost, a to tím
více, čím přesněji se snažíme polohu stanovit (přesné změření polohy částice může naprosto
"rozhodit" její hybnost!). Pro
přesnější lokalizaci polohy částečky musí být vlnová
délka ozařujícího vlnění dostatečně krátká, tj. energie
a hybnost kvant je patřičně vyšší - způsobuje citelnější narušení
pozorovaného systému (polohy a rychlosti částečky).
Zde již nebudeme pozorovat
přímo očima, ale prostřednictvím přístroje
(např. mikroskopu vč. mikroskopu
elektronového, detektoru částic, radiometru, spektrometru), přičemž pro pozorování částic velmi malých
rozměrů je třeba použít záření o patřičně krátké
efektivní vlnové délce. Subjektivní úloha pozorovatele
se v souvislosti s kvantovou mechanikou často přeceňuje
(pochází to z dob vzniku kvantové
fyziky) a někdy se dokonce zpochybňuje
objektivní realita jako taková. To je nedorozumění!
Přírodní děje s nespočetnými interakcemi částic a polí
neustále probíhají v přírodě spontánně a jejich výsledky
jsou nezávislé na nás. Pouze naše občasné
sondy do dějů mikrosvěta jsou zatíženy principiálními
kvantovými neurčitostmi. Není to však důsledek našeho
subjektivního zásahu jako vědomého pozorovatele, ale vliv interakce
objektivně existujících částic s čidly a přístroji,
použitými pro pozorování či měření (je
ještě stručně diskutováno níže v pasáži "Mystická
kvantová fyzika?").
Často uváděné tvrzení že "pozorování
vytváří realitu" je zavádějící a chybné:
ta realita zde byla již předtím, pozorování nám ji
jen "osvětlilo" - a mohlo ji i změnit, v důsledku
kvantového ovlivnění na mikroskopické úrovni.
Abychom tedy mohli "pozorovat" a měřit
nějakou mikročástici, musíme od ní nechat odrazit
nějakou další částici či kvantum záření a pozorovat
teprve výsledek tohoto odrazu - obecněji výsledek
interakce. Nevyhnutelným důsledkem takového procesu
je to, že kolize či interakce
nenávratně změní stav sledované částice -
odchýlí ji, změní její rychlost, popř. dokonce vnitřní
strukturu. Obecně: abychom uskutečnili pozorování nějakého
objektu či systému, musíme s ním interagovat.
Pouze v tomto smyslu lze realitu v mikrosvětě ovlivnit
pouhým "pozorováním"!
Operace (procesy) pozorování nebo měření tedy
nutně ovlivňují fyzikální systém
(narušují jeho evoluci), přičemž pro malé systémy *) je toto narušení značné a
nevratné, má principiální charakter a nelze
jej nijak eliminovat či zkorigovat; a to žádnou zdokonalenou
metodou - je vlastní podstatě věci samotné!
Kvantová mechanika se zabývá právě chováním takových
systémů a procesy měření jejich fyzikálních veličin.
*) V mikrosvětě pojem "malý"
ztrácí svůj obvyklý relativní charakter a stává se
objektivním absolutním atributem, určujícím
kvantové chování daného systému.
"Pozorovatel"
bývá v interpretaci kvantové mechaniky jedním z nejvíce
nepochopených pojmů (vedle
stochastičnosti, interference stavů či kolapsu vlnové
funkce...). Z objektivního hlediska je pozorovatel
nějaký "klasický" (nekvantový) objekt *), který interaguje s daným
systémem, zde kvantovým, za účelem prozkoumání některé
jeho vlastnosti. Podle druhu zkoumaného jevu a experimentální
konfigurace může tímto "pozorovatelem" být
elektronický či optický měřící přístroj, mechanické
těleso, potažmo pak člověk (nebo i
jiný biologický organismus...). Jako
výsledkek interakce pak můžeme získat vlatní hodnotu
určitého kvantového čísla.
*) Každý takový "klasický"
pozorovatel je vnitřně též složen z obrovského počtu
kvantových částic, avšak jejich fluktuace se zprůměrují,
takže pro všechny praktické účely se chovají jako
klasické...
Kvantová teorie: ontologická
fyzika + gnoseologické měření
V kvantové fyzice se úzce, ve zpětné vazbě, prolínají dva
aspekty, které se z filosofického hlediska nazývají ontologický
(jaká je skutečná fyzikální realita) a gnoseologický (jak
poznávat tuto realitu) :
--> Na základě zkušeností z klasické mechaniky a
elektrodynamiky si vytváříme modely studovaných systémů,
zobecněné tak aby odpovídaly specifickým zákonitostem
atomové, jaderné a částicové fyziky.
--> Tyto částice a pole necháme interagovat s klasickým
měřícím systémem a monitorujeme jeho odezvu.
Právě tento jediný možný způsob měření
produkuje pozorované stochastické kvantové zákonitosti ....
Mystická kvantová fyzika - "kvantová
mystika" ?
Kvantová fyzika bývá z filosofického hlediska často falešně
interpretována. Ze shora uvedeného faktu, že realitu
v (mikro)světě lze ovlivnit pozorováním, se vyvozují mystická
tvrzení, že "lidská mysl vytváří realitu",
nebo "kvantová mechanika spojuje mysl člověka s
vesmírem", popř. "kvantová fyzika
vytváří jenotu lidského a kosmického vědomí", je
podstatou "svobody vůle" a pod. Základní
omyl či nedorozumění zde opět vyplývá z výše uvedeného
přeceňování a nepochopení úlohy subjektivního
"vědomého" pozorovatele. Není
to naše mysl, co uskutečňuje pozorování, nýbrž
samotné interakce základních částic, které
probíhají i bez nás. Tyto interakce totiž
pozměňují kvantový stav systémů a přenášejí
"informace", naše mysl je pouze registruje a
zpracovává. Ve skutečnosti je to objektivní realita,
jejíž zákonitosti (včetně kvantových) určují chování naší mysli i fungování celého
vesmíru. Tento přístup odpovídá všem dosavadním
výsledkům našich pozorování, je s nimi plně konzistentní.
Poznatky, že při některých jevech v
mikrosvětě je narušována kauzalita a determinismus,
vedly k hypotetickému spojování kvantové fyziky se svobodnou
vůlí. Máme určitý oprávněný pocit svobodné
vůle - že můžeme rozhodnout co budeme dnes dělat, či co si
naplánujeme na zítřek; že to záleží především na nás,
nerozhodují o tom pouze vnější okolnosti. Skutečná
svobodná vůle je však z hlediska přírodovědy možná jen iluze.
Především nemůžeme dělat něco, co odporuje přírodním
zákonům; a i jiné věci, kterým brání určité další
okolnosti... "Svoboda vůle" se vynořuje z
nepřeberných množství interakcí a jejich výsledků,
nepotřebujeme pro ni kvantovou fyziku (viz
též diskusi v části "Determinismus-náhoda-chaos ?" §3.3 v knize "Gravitace,
černé díry a fyzika prostoročasu")..?..
Kvantová mystika
je souhrn různých podivných představ, které se pokoušejí spojit
špatně pochopené aspekty kvantové fyziky se stejně špatně
pochopenými názory o vědomí. Žádné reálné opodstatnění
zde není, děje se tak jen ve fantazii některých lidí...
Nekonečně mnoho
paralelních vesmírů ?
Ze stochastičnosti chování částic a systémů podle
kvantové fyziky rovněž vznikla poněkud fantaskní hypotéza H.Everetta
o nekonečném množství vesmírů: při
každém pokusu o zjištění reality - při každé interakci
částic - se celý vesmír rozdělí, rozvětví či "zduplikuje"
na dva nebo několik dalších "vesmírů", v nichž se
uskuteční jednotlivé možné výsledky interakce (s příslušnou pravděpodobností). Vzniká tak neustále nekonečné množství "paralelních
světů", v nichž všechny možné alternativní
budoucnosti (a minulosti) jsou "skutečné"..?..
V některých takových
vesmírech by např. asteroid před 60 miliony let minul naši
planetu a na Zemi by dosud vládli dynosauři (či by dokonce
vytvořili civilizaci místo lidí)..?..
Pro nás dostupný (tj. "skutečný") je
však pouze ten vesmír, v jehož stavu se v daném okamžiku
nacházíme; pozorování lze provádět pouze v "našem
světě". Alternativní děje v paralelních vesmírech si
lze jen představovat...
Vyskytly se i sci-fi
hypotézy, že paralelní vesmíry se mohou na kvantové
mikro-úrovni ovlivňovat (působit tedy i na
náš svět). Jejich kvanta (částice) mohou mezi jednotlivými
vesmíry "prosakovat" a vyvolávat některé
"bizarní" efekty kvantové mechaniky..?..
Všechno jsou to jen nepodložené doměnky...
O astronomických a
filosofických souvislostech více vesmírů - multiverza
- viz např. práci "Antropický princip aneb
kosmický Bůh", nebo
§5.7 "Antropický princip a existence více vesmírů" monografie "Gravitace, černé díry a
fyzika prostoročasu".
V
mikrosvětě záleží na pořadí úkonů při
měření. Např. na tom, zda změříme nejprve polohu částice
(tím narušíme hybnost) a pak teprve její stávající
hybnost, nebo naopak (změřením hybnosti nejprve narušíme
polohu). Čím přesněji změříme polohu, tím méně přesně
známe hybnost částice - a naopak. Vede to k pricipiální nekomutativnosti
kvantové mechaniky, vyjádřené v kvantových relacích
neurčitosti (viz níže).
Pod pojmem "stav" fyzikálního
systému se rozumí situace, kdy se tento systém
nachází v konfiguraci (stavu) s určitou hodnotou dané
fyzikální veličiny. V klasické fyzice je např. stav
částice popsán zadáním polohy a rychlosti resp. hybnosti
(jako funkce času). V kvantové fyzice je situace
složitější, zavádí se zde tzv. vektor stavu,
značený |y>, kde y jen symbolicky označuje stavovou veličinu, která
však nemusí mít určitou hodnotu, ale může být superpozicí
několika stavů. Např. elektron se z hlediska spinu (viz níže) může nacházet ve
stavu |1> se spinem
orientovaným "nahoru" (z-komponenta projekce spinu má
hodnotu +1/2h), nebo ve stavu |2> se spinem -1/2h. Může se však
nacházet i v obecnějším stavu |y>, který je
"smíšenou" superpozicí
"čistých" stavů |1> a |2>, což se vektorově zapisuje: |y> = a1.|1> + a2.|2> . Tento stav |y> znamená, že s pravděpodobností a12
naměříme hodnotu +1/2h a s
pravděpodobností a22 naměříme hodnotu -1/2h. Obecně může
být superponovaný stav tvořen více komponentami: |y> = a1.|1> + a2.|2> + ... + ai.|i> + ... Obecný |y> je tedy stav, kde daná fyzikální veličina nemá
určitou hodnotu, ale pouze pravděpodobnost ai2 naměření
jednotlivých potenciálních hodnot "i". Kvantová
fyzika je matematický algoritmus (výpočetní
schéma), který dokáže stanovit tyto koeficienty ai - avšak
nespecifikuje vnitřní fyzikální podstatu těchto jevů. Ve
stavu |y>, před měřením, má systém hodnotu dané
fyzikální veličiny neurčitou (jsou potenciálně
možné různé hodnoty) a teprve měřením se tato hodnota konkretizuje.
I při stejných výchozích podmínkách naměříme pokaždé různé
hodnoty fyzikálních veličin, statisticky rozdělených kolem
středních hodnot určených pravděpodobnostními koeficienty ai2.
Operátory.
Relace neurčitosti.
Operace pozorování či měření se v kvantové mechanice
modelují pomocí tzv. operátorů. Každé fyzikální
veličině A je v kvantové mechanice přiřazen operátor
A^, který
splňuje určité matematické podmínky (je lineární a
hermitovský). Operátorem ^A rozumíme předpis, který každé funkci u(x)
přiřazuje nějakou jinou funkci v(x) - symbolicky píšeme v = ^A u. Operátor ^x přiřazený
souřadnici x je prosté násobení x, zatímco
operátor hybnosti ^p je dán derivací podle souřadnice x :
^x ® x , ^p ® - i h . ¶/¶x .
Planckova konstanta h se zde dostala proto, aby platil vztah mezi hybností
částice a odpovídající frekvencí Broglieovy vlny v
korpuskulárně-vlnovém dualismu. Další fyzikální veličiny
- energie a moment hybnosti - budou diskutovány níže.
Pro operátory v kvantové mechanice je
důležité, že postupná aplikace dvou operátorů nemusí být
komutativní, tj. může záležet na pořadí. Pro dva
operátory ^A a ^B se definuje tzv. komutátor vztahem [
^A ,^B] = ^A^B - ^B^A,
tj. rozdíl aplikace operátoru ^A a pak ^B, minus tytéž operátory aplikované v opačném
pořadí. Tento rozdíl přitom není obecně roven nule jako v
klasické fyzice, neboť každé pozorování (měření) v
mikrosvětě může vyvolat poruchu systému a tím ovlivnit
výsledek druhého pozorování (měření), takže tyto dva
postupy mohou poskytnout rozdílné výsledky. Operátory
souřadnice a hybnosti splňují důležitou komutační relaci [^x , ^p] = i . h .
Tato komutační relace souvisí s klíčovým
principem kvantové mechaniky, s tzv. Heisenbergovým kvantovým
principem neurčitosti, který říká, že polohu x
a hybnost p částice nelze současně
stanovit zcela přesně *), ale že neurčitosti těchto dvou
(komplementárních) veličin jsou dány relací Dx . Dp ł h. Každé
měření polohy částice nenávratně narušuje její hybnost -
a naopak. Nelze tedy vyšetřovat přesnou konkrétní dráhu, po
níž se částice pohybuje...
*) Kvantová
"rozmazanost", implikovaná relacemi neurčitosti, je v
makroskopickém světě většinou zanedbatelná a
nepozorovatelná, avšak v atomárním a subatomárním
měřítku se stává naprosto rozhodující!
Tato kvantová neurčitost je vyjádřením
základní vlastnosti pozorování a měření: že se vždy
jedná o interakci, nevratně ovlivňující
parametry měřeného systému. Stejné relace neurčitosti
platí i mezi dalšími dynamicky zpřaženými
veličinami, např. mezi časem t a energií E:
DE . Dt ł h, dále mezi
potenciální a kinetickou energií atd. Tato komplementarita,
jejímž "prototypem" je korpuskulárně-vlnový
dualismus, je pro kvantovou fyziku charakteristická.
Charakteristické
rovnice. Diskrétní hodnoty fyzikálních veličin.
Při aplikaci operátorů na vlnové funkce jsou obzvlášť
důležité případy, kdy výsledkem operátoru ^A aplikovaného na
funkci y(x)
je opět tatáž funkce y(x) vynásobená určitým číslem a: ^Ay(x) = a. y(x). Obecně ke
každému operátoru ^A přísluší množina čísel an a množina funkcí yn, pro něž platí
tzv. charakteristická rovnice
^A
yn(x) = an . yn(x) .
Čísla (koeficienty) an se nazývají vlastní
(charakteristické) hodnoty a yn odpovídající vlastní (charakteristické) funkce
operátoru ^A. Vlastní hodnoty an operátoru ^A představují pak možné hodnoty,
jichž může fyzikální veličina a odpovídající
operátoru ^A nabývat. Uvedená rovnice je diferenciální rovnicí
pro vlnovou funkci toho stavu, v němž má veličina
reprezentovaná operátorem ^A hodnotu a. Vlastní hodnoty splňující tuto
rovnici nenabývají obecně všech možných hodnot, ale jen
určitých diskrétních hodnot, v souhlase s
experimentálními poznatky o diskrétních (kvantových)
hodnotách fyzikálních veličin v mikrosvětě - energie
atomů, magnetické momenty, spiny ... Ukazuje se, že
energeticky (polně) vázaným částicím v mikrosvětě
přísluší diskrétní hodnoty energie, hybnosti a dalších
veličin - nazýváme je kvantové fyzikální veličiny.
Tyto diskrétní charakteristické hodnoty, vyjádřené jako
násobky své příslušné elementární hodnoty (většinou
Planckovy konstanty h), se nazývají kvantová čísla.
Kvantová
energie. Schrödingerova rovnice.
Podobně jako v klasické, tak i v kvantové mechanice je
klíčovým pojmem energie E. Energii E
(skládající se z potenciální energie U a kinetické energie
T: E = T + U) je v kvantové mechanice přiřazen operátor
energie zvaný Hamiltonův operátor, který pro
nejjednodušší případ částice hmotnosti m má tvar
^H
= -(h2/2m). D + U ,
kde D ş ¶2/¶x2
+ ¶2/¶y2
+ ¶2/¶z2
je tzv. Laplaceův diferenciální operátor. Vlastní
(charakteristická) rovnice Hamiltonova operátoru
^H
yn = En . yn
se nazývá stacionární Schrödingerova
rovnice. Jejím řešením pro částici jsou vlnové
funkce stacionárních stavů částice v potenciálovém poli, v
němž částice nabývá diskrétních hodnot energie En (o
spojitých a diskrétních hodnotách energie viz poznámku
níže).
Časový vývoj (pohyb) kvantového stavu mikročástice pak
popisuje nestacionární Schrödingerova rovnice
^H
y = i h . ¶y/¶t ,
která obsahuje časovou derivaci vlnové funkce.
Řešení stacionární Schrödingerovy rovnice udává,
jaké možné stacionární fyzikální stavy
může částice v daném silovém poli nabývat, pomocí
nestacoionární Schrödingerovy rovnice lze v principu zjistit pravděpodobnosti,
s nimiž částice přecházejí z jednoho
kvantového stavu do druhého. Lze říci, že Schrödingerova
rovnice má v kvantové mechanice podobné postavení, jako mají
Newtonovy zákony v mechanice klasické. Plynou z ní mimo jiné
i všechny kvantové vlastnosti stavby atomů, které budou
diskutovány níže (především diskrétní energetické
hladiny).
Energie
spojitá a diskrétní - kvantovaná
V klasické fyzice může energie nabývat spojitě všechny
možné hodnoty, konáním práce lze energii těles v určitém
systému libovolně měnit. V kvantové fyzice je situace
složitější. Hodnoty energie jsou řešením (stacionární)
Schrödingerovy rovnice uvedené výše. V nejjednodušším
případě volné částice (U=0) má tato
rovnice tvar (h2/2m). Dy + E.y = 0 a jejím řešením
jsou vlnové funkce tvaru y = const. ei/h(E.t-p.r), pro libovolné hodnoty energie E, přičemž E = p2/2m. Každá taková
funkce (rovinná vlna) popisuje stav, v němž částice nabývá
určitou hodnotu energie E a hybnosti p,
přičemž frekvence takové vlny je E/h a vlnová délka l = 2ph/p je Broglieho vlnová délka částice. Energetické
spektrum volně se pohybující částice je tedy spojité,
energie může nabývat hodnot od 0 do Ą - energie volné částice
není kvantována.
Nachází-li se částice v potenciálovém poli U(x,y,z),
pak pohyb vázané částice s energií E<0
má diskrétní spektrum energetických hladin,
zatímco pro kladné energie není částice vázána a její
energie může nabývat spojité spektrum. Typickým modelovým
případem kvantového pohybu vázané částice je pohyb
částice v potenciálové jámě - v
nejjednodušším případě jednorozměrný pohyb vázaný na
úsečku délky L mezi dvěma kolmými stěnami (nekonečně
vysokými), od nichž se částice dokonale pružně odráží.
Takovému pohybu částice po úsečce přísluší Broglieova
vlna, která se na stěnách odráží, přičemž superpozicí
vln odražených od obou stěn vzniká "stojaté
vlnění". Na úsečce délky L se tak vytvoří celistvý
počet půlvln stojatých Broglieových vln, tj. L = n.l/2, kde n=1,2,3,...
Pohybu částice v potenciálové jámě tedy odpovídají jen
určité diskrétní hodnoty vlnových délek
Broglieových vln ln = 2.L/n, n=1,2,3,...
Broglieova vlnová délka souvisí s hybností částice, l = h/p, takže i hybnost
vázané částice pn = h/ln = n.h/L a její energie
En = pn2/2m = n2.h2/8m.L2 budou mít diskrétní
hodnoty *). Stav částice v potenciálovém poli,
které odpovídá stojatá Broglieova vlna ln, představuje určitý stacionární stav
částice. Je to stav s určitou energií En - energetickou hladinou částice v
potenciálovém poli v daném stacionárním stavu. Číslo n
pak označujeme jako kvantové číslo tohoto
stacionárního stavu. Stav odpovídající n=1 se nazývá základní
stav a odpovídá mu nejnižší hladina energie
částice vázané v potenciálovém poli. Změna energie
částice je spojena s přechodem (překokem) do
jiného stacionárního stavu, což je doprovázeno vyzářením
nebo pohlcením kvanta (fotonu) o energii rovné
rozdílu energií obou stacionárních stavů (energetických
hladin). Tyto zákonitosti nacházejí své uplatnění níže v Bohrově
modelu atomu.
*) Při velkých hodnotách
kvantových čísel n vycházejí rozdíly
energie jednotlivých kvantových stavů s kvantovými čísly
n+1 a n malé - poměr En+1/En = [(n+1)2-n2]/n2 se blíží 1. Tedy změny energie na jednotlivých
vyšších kvantových hladinách energie jsou zanedbatelné -
energii zde můžene považovat za spojitou; výsledky kvantové
mechaniky při vyšších kvantových číslech v podstatě
odpovídají výsledkům klasické mechaniky - princip
korespondence.
Skutečné energetické spektrum částic v mikrosvětě
může být diskrétní i spojité, v závislosti na procesu,
při nichž částice vznikají, získávají energii a jsou
emitovány. Spojité energetické spektrum má
např. brzdné záření, záření b, Comptonovsky rozptýlené
záření g. Jiná spektra jsou diskrétní,
kvantovaná, čárová - např. záření a a g, spektra záření
excitovaných atomů, charakteristické X-záření, konverzní
či Augerovy elektrony. Určitým přechodem mezi spojitým a
diskrétním spektrem jsou pásová spektra, kdy
jednotlivé kvantové stavy jsou odděleny jen velmi malými
energetickými intervaly a výsledné spektrum se v rámci
rozlišení spektrometrických přístrojů jeví jako spojité. Konkrétní mechanismy emise částic a získávání
energie budou podrobněji rozebírány při popisu záření
atomů a atomových jader při radioaktivitě a dalších
procesech.
Dovolené a zakázané
přechody
Z hlediska klasické fyziky mohou probíhat jen takové děje,
při nichž jsou na všech etapách splněny zákony
zachování energie, hybnosti, momentu hybnosti. Takové
děje, zvané dovolené přechody, samozřejmě
mohou probíhat i podle kvantové fyziky v mikrosvětě.
Probíhají velmi "ochotně", jejich rychlost
(efektivní doba trvání přechodu, přeměny, interakce)
závisí na druhu síly která ji způsobuje. Nejrychlejší jsou
přechody způsobené silnou interakcí, následují
elektromagnetické děje a nakonec přeměny způsobené slabou
interakci.
V mikrosvětě však mohou probíhat i některé
takové děje, u nichž jsou na některých etapách
tyto klasické zákony zachování porušeny - tzv. zakázané
přechody. Můžeme si to zjednodušeně představit
tak, že částice (v rámci svého
permanentního kvantového kmitání a fluktuací) to neustále znova a znova "zkouší", až se
jí podaří "prorazit" bariéru zákazu. Vlnová
funkce částice je rozprostřena ve fázovém prostoru a
částečně může zasahovat i do oblastí, kde přechod může
"obejít" porušení zákona zachování. Zakázané
přechody tak mohou v zásadě probíhat, ale s menší
pravděpodobností. Typickým případem je níže
popsaný tunelový
jev průchodu částice
energetickou bariérou, nebo zakázané přechody mezi
energetickými hladinami elektronů v obalu (viz níže "Excitace a
záření atomů") či mezi
energetickými hladinami nukleonů v jádře (§1.2, část
"Radioaktivita
gama", pasáž "Jaderná
izomerie a metastabilita") z důvodu vyšších
rozdílů momentu hybnosti (multipolarit) než je schopen odnést
emitovaný foton.
Kvantový moment hybnosti. Spin. Magnetický
moment.
Jednou z důležitých fyzikálních charakteristik pohybu
hmotných těles v prostoru je moment hybnosti -
vektorová veličina kvantifikující především rotační
pohyb těles. Zákon zachování momentu hybnosti *)
poskytuje řadu užitečných údajů o vlastnostech pohybu.
*) Zákon zachování momentu hybnosti je
důsledkem invariance fyzikálních zákonů (Hamiltoniánu
soustavy) vůči prostorové rotaci o libovolný
úhel - izotropie prostoru. Tato vlastnost platí nejen ve
volném prostoru bez polí, ale i při pohybu v centrálně
symetrickém poli, kde ovšem invariance vůči rotaci platí pro
rotaci kolem středu pole. Moment hybnosti proto hraje
důležitou úlohu při sledování pohybu planet i při analýze
pohybu elektronů kolem atomového jádra v jeho centrálním
poli.
Moment hybnosti částice (hmotného bodu) v klasické
mechanice je vektorová veličina L, která je
definována jako vektorový součin polohového vektoru r
a vektoru hybnosti p: L = [r´p],
neboli ve složkách ve směru osy x,y,z: Lx= y.pz - z.py, Ly= z.px - x.pz, Lz= x.py - y.px. Náhradou složek souřadnic a hybnosti výše
zmíněnými operátory obdržíme operátory složek momentu
hybnosti: ^Lx= h/i
(y.¶/¶z - z.¶/¶y), ^Ly= h/i (z.¶/¶x - x.¶/¶z), ^Lz=
h/i (x.¶/¶y - y.¶/¶x). Vektorově to lze zapsat ^L = [^r´^p] =
-ih [r´Ń],
kde Ń je vektorový tvar Hamiltonova diferenciálního
operátoru. Charakteristickou rovnici pro moment hybnosti je
zvykem (bez újmy na obecnosti) vyšetřovat pro složku z: ^Lzy = lz .y, a to ve
sférických souřadnicích r,J,j. Její řešení je (matematické
podrobnosti zde nemůžeme uvádět): y = f(r,J).eilzj, kde
f(r,J)
je libovolná funkce poloměru r a úhlu J. Aby
charakteristická funkce y byla jednoznačná, musí být periodická vzhledem k j s periodou 2p, takže musí být
:
lz = m . h , kde m = 0, ±1, ±2, ....
Vlastní hodnoty momentu hybnosti lz jsou tedy kvantovány - mohou se
rovnat kladným a záporným celým násobkům Planckovy
konstanty h včetně nuly. Tento výsledek je důležitý tím, že
kvantově-mechanicky zdůvodňuje základní Bohrův
postulát modelu atomu, který je níže rozebírán ("Bohrův model atomu").
Vedle složek momentu hybnosti L je v
mechanice důležitá i jeho absolutní velikost L ş |L|
= Ö(L2). Charakteristické
hodnoty K čtverce momentu hybnosti jsou určeny rovnicí ^L2y = K .y. Poměrně
složitým a zdlouhavým matematickým rozborem (využívá se zde m.j. opět požadavku jednoznačnosti
charakteristické funkce y vedoucí k periodicitě 2p) lze
pro charakteristické hodnoty čtverce momentu hybnosti obdržet
formuli
K = h2. l (l + 1) , l =
0, 1, 2, ...
Charakteristické hodnoty operátoru absolutní velikosti momentu
hybnosti |L| pak jsou :
|L| = h. Ö[l (l + 1)] , l = 0, 1,
2, ...
Při dané hodnotě čísla L může složka momentu
hybnosti Lz
nabývat hodnoty Lz = L, L-1, L-2, ... ,0, -1, ..., -L, tj. celkem 2.L+1
různých hodnot, odpovídajících různým orientacím momentu
hybnosti v prostoru. Všechna tato pravidla se uplatňují m.j.
ve struktuře elektronového obalu atomu, kde energetická
hladina odpovídající momentu hybnosti L je (2.L+1)-krát
degenerovaná; ve spojení s Pauliho principem to implikuje
obsazovací pravidla pro elektronové hladiny, jak je popsáno
níže.
S p i n
V klasické mechanice se vedle vzájemného momentu hybnosti
pohybujících se těles, či momentu hybnosti tělesa vzhledem k
danému bodu, uplatňuje i vlastní (vnitřní)
moment hybnosti způsobený rotací
tělesa kolem vlastní osy. V kvantové mechanice moment hybnosti
určuje symetrii stavu systému vzhledem k rotaci v prostoru, tj.
způsob, jak se při pootočeních souřadnicové soustavy
vzájemně transformují vlnové funkce odpovídající různým
hodnotám průmětu momentu hybnosti. Na původu momentu hybnosti
zde již nezáleží. Rozbor vlastností částic ukazuje, že v
kvantové mechanice musíme i elementární částici připsat
určitý vlastní moment hybnosti, který
nesouvisí s jejím pohybem v prostoru. Vlastní moment hybnosti
částice se nazývá spin a značí se s,
zatímco moment hybnosti související s pohybem částice v
prostoru se označuje jako orbitální moment (značí
se většinou L nebo l). Tato vlastnost
elementárních částic má specificky kvantovou povahu a nelze
ji vysvětlit pomocí klasických mechanických představ (spin
nelze kvantitativně vysvětlit např. rotací částice kolem
vlastní osy!) *). Při kvantovém popisu částice se spinem
musí vlnová funkce určovat nejen pravděpodobnost různých
poloh jejího výskytu v prostoru, ale i pravděpodobnost
různých orientací spinu. Vlnová funkce musí tedy záviset
nejen na třech prostorových souřadnicích, ale i na spinové
proměnné, která udává hodnotu průmětu spinu do určitého
směru v prostoru (volí se osa z) a nabývá omezený
počet diskrétních hodnot.
*) Rozdílnost spinu od
orbitálního momentu hybnosti
Spin kvantových částic se v některých svých vlastnostech
značně liší od obvyklého orbitálního či
vlastního rotačního mechanického momentu hybnosti těles :
->
Je kvantován, nabývá určité
diskrétní hodnoty (zmíněné níže); to je však v obecném
souladu s kvantovou fyzikou (takže to
není překvapivé).
-> Pro daný druh elementární částice má spin přesně
danou hodnotu (v násobcích Planckovy konstanty);
částici nelze nijak "donutit" aby rotovala rychleji
či pomaleji. Hodnota spinu závisí pouze na typu částice a
nelze ji žádným způsobem změnit (na rozdíl od orbitálního
momentu hybnosti či směru spinu)...
-> Spin kvantových částic může nabývat hodnoty 0,
1/2, 1, 3/2, 2, ... - násobku Planckovy konstanty. Naproti tomu
orbitální moment hybnosti může nabývat pouze celočíselné
hodnoty násobku Planckovy konstanty.
Podobně jako moment
hybnosti obecně, i spin je kvantován. Vlastní
hodnoty druhé mocniny spinu se rovnají s2 = h2. s(s + 1), kde spinové číslo s
může být celé (včetně nuly) nebo poločíselné; je
vnitřní charakteristikou daného druhu částice. Při daném s
může průmět spinu nabývat hodnot sz = -s, -s+1, ...., s-1, s , celkem tedy 2.s + 1 hodnot. V §1.5 "Elementární částice",
pasáž "Nerozlišitelnost částic"
- "Spin, symetrie vlnové funkce a statistické
chování částic", uvidíme, že se vyskytují dvě hlavní skupiny
částic podle spinu s: částice s poločíselným
spinem (těch je většina - elektrony, protony,
neutrony, miony atd.) a s celočíselným spinem
(fotony, p a K mezony, hypotetické gravitony a další). Tato
okolnost těsně souvisí s kvantovým chováním souborů
částic - částice se zde chovají jako fermiony
nebo bosony (§1.5,
pasáž "Fermiony-Bosony").
Magnetický moment
Každé elektricky nabité těleso ("náboj",
"nabitá částice") vzbuzuje v
okolním prostoru elektrické pole podle Coulombova
zákona (pokud je nabitá částice v
klidu vůči vztažné soustavě, jedná se o elektrostatické
pole). Když se nabité těleso pohybuje
rovnoměrně přímočaře, vzbuzuje kromě toho i magnetické
pole podle Biot-Savart-Lapleceova zákona. A
jestliže se náboj pohybuje nerovnoměrně - zrychleně či po
zakřivené dráze, budí kolem sebe časově proměnné
elektromagnetické pole, jehož část se prostorem šíří jako
elektromagnetické vlnění. Tyto základní
poznatky sjednocené nauky o elektřině a magnetismu - elektrodynamiky
(viz např. §1.5 "Elektromagnetické pole. Maxwellovy rovnice." v knize "Gravitace, černé díry a
fyzika prostoročasu"), dokonale
fungují nejen v klasické, ale i v relativistické a kvantové
fyzice.
Pomineme-li translační pohyb (zde irelevantní) a vyzařování
vln (kterým se budeme zabývat níže), je hlavním mechanismem buzení magnetického pole
nabitými částicemi jejich rotační pohyb.
Pohyb nabité částice po kruhové dráze generuje magnetické
pole, jehož směr je kolmý k rovině oběhu a jehož intenzita
(mag. indukce) je úměrná náboji částice a momentu hybnosti
jejího oběhu. Toto magnetické pole se chová jako fiktivní magnetický
dipól - miniaturní "tyčový magnet". Jeho
síla se kvantifikuje pomocí vektorové veličiny magnetický
moment m, vyjadřující moment dvojice sil f,
který by působil na tento magnetický dipól ve vnějším
homogenním magnetickém poli B: f
= [m´B]. Částice s nábojem q a
klidovou hmotností m, která rotuje s úhlovým momentem
hybnosti L, podle klasické elektrodynamiky
generuje magnetický dipólový moment m = (q/2m) .
L . V oblasti buzení magnetického pole
rotačním pohybem nabitých těles se často zavádí tzv. gyromagnetický
poměr g, což je poměr buzeného magnetického momentu a
mechanického momentu hybnosti rotujícího tělesa. Pro
klasické nabité rotující těleso je g = q/2m .
Rotační pohyb nabitých částic, budící
magnetický moment, může být dvojího druhu:
-> Oběžný (orbitální) pohyb
nabité částice v poli vazbových sil s jinými částicemi. To
je případ elektronů obíhajících kolem atového jádra.
Elektron klidové hmotnosti me, obíhající s momentem hybnosti L,
se chová jako magnetický dipól s momentem m =
g.(-e/me). L.
Většinou se však vyjadřuje ve tvaru m = -g.mB . L/h , kde mB = e.h/me je tzv. Bohrův magneton.
Bezrozměrný korekční faktor g udává vztah mezi
skutečně pozorovaným magnetickým momentem částice a
teoretickou hodnotou Bohrova magnetonu.
-> Vlastní rotační pohyb nabité
částice, otáčející se kolem své osy - shora zmíněný spin
částice. Výše uvedený klasický vztah m = (q/2m).L
pro buzení magnetického momentu v zásadě platí i tehdy,
když moment hybnosti L vzniká rotací tělesa
se stejně rozloženou hustotou hmotnosti a elektrického náboje
kolem vlastní osy symetrie. Spinový magnetický moment
elektronu lze vyjádřit jako: ms = -gs.mB . S/h , kde S
je spinový moment hybnosti elektronu (+,-1/2 h). g-faktor je zde
přibližně roven 2.
Složitější situace je u nukleonů
- protonů a neutronů. Přímočarou analogií s elektrony
bychom pro magnetický moment protonu obdrželi
vztah mp = gp.mN . S/h
, kde mN je tzv. jaderný magneton mN = e.h/mp . Korekční faktor g
zde však má poměrně vysokou hodnotu
hodnotu gp=5,58; to naznačuje, že stanovení mag. momentu
protonu na základě jeho spinu je problematické (viz níže). Proton má tedy magnetický
moment mp
= 1,41.10-26J/T a gyromagnetický poměr
gp = 2,675.108 rad.s-1.T-1. Gyromagnetický poměr m.j. udává frekvenci Larmorovy
precese magnerického momentu částic ve vnějším
magnetickém poli; pro protony tedy Larmorova frekvence činí
42,577 MHz/T - využívá se v analytické a zobrazovací metodě
nukleární magnetické rezonanci (viz §3.4, část "Nukleární magnetická rezonance"). Neutron,
jakožto elektricky neutrální (nenabitá) částice by neměl
mít žádný magnetický moment, mělo by být mn = 0. Ve skutečnosti však neutron má
nenulový magnetický moment mn = -0,97.10-26J/T, který je jen o něco menší než
u protonu (a má opačné znaménko). Jak je to možné?
Původ magnetického momentu nukleonů totiž
nespočívá v jejich rotačním momentu hybnosti (spinu),
nýbrž pochází z jejich vnitřní struktury -
že jsou složeny z kvarků "u" a
"d" (§1.5, pasáž "Kvarková struktura hadronů"). U hypotetických či
modelových kvarků se předpokládá magnetický moment m"u" a m"d", který v
prvním přiblížení může být modelován podobným způsobem
jako jaderný magneton: mq = qq.h/mq . Magnetický moment
nukleonu pak můžeme považovat za složený z vektorového
součtu magnetických momentů tří nabitých kvarků a
orbitálních magnetických momentů způsobených pohybem
těchto nabitých kvarků v nukleonu. Pomocí kvarkového modelu
magnetický moment protonu (složeného
ze 2 kvarků "u" o nábojích +2/3e
a 1 kvarku "d" s nábojem -1/3e)
pak můžeme přibližně vyjádřit jako mp = 4/3m"u"-1/3m"d" = 2,8.mN = 1,41.10-26J/T. A magnetický
moment neutronu (složeného
ze 2 kvarků "d" o nábojích -1/3e a 1 kvarku
"u" s nábojem+2/3e) pak činí mn = 4/3m"d"-1/3m"u" = -1,9.mN = -0,97.10-26J/T. O
detailnější analýzu, zahrnující gluonová pole a
virtuální částice uvnitř nukleonů, se snaží kvantová
chromodynamika (není dosud završeno).
Kvantová
teorie pole
Kvantovým chováním mikrosvěta jsme se zde zatím zabývali z
pohledu kvantové mechaniky pohybu
mikročástic: hmotným částicím se přiřazují vlny
pravděpodobnosti (tvořící pole) a řešením příslušných
vlnových rovnic se obdrží specifické kvantové
vlastnosti pohybu částic, zahrnující diskrétní
hodnoty energie a dalších fyzikálních veličin. Kvantování
tohoto druhu se někdy označuje jako "prvotní".
Vedle částic je hlavním předmětem
přírodovědného popisu fyzikální pole.
Fyzikální pole, které je nositelem energie, hybnosti a
dalších fyzikálních parametrů, stejně jako částice, musí
mít v mikrosvětě rovněž kvantový charakter. Při kvantovém
popisu polí, zvaném někdy druhotné kvantování,
se naopak pole vyjadřuje pomocí částic -
kvant excitací v poli. Přechod od klasické ke kvantové teorii
pole sestává ze dvou základních etap :
Použití této metody kvantování na
elektromagnetické pole je základem kvantové
elektrodynamiky (QED) a vede k představě
elektromagnetického pole jako souboru částic - fotonů,
z nichž každá má energii h.w a hybnost h.w/c; klidová
hmotnost fotonů je nulová, jejich spin (vlastní moment
hybnosti) je roven 1 (resp. 1.h). Přitom tato elektromagnetická
kvanta (fotony) jsou interpretovány jako částice,
zprostředkující interakci elektricky nabitých částic.
Vyzařování a pohlcování fotonů elektrickými náboji
(především elektrony) se vyjadřuje pomocí tzv. kreačních
a anihilačních operátorů, které vytvářejí či
odebírají fotony v určitém energetickém stavu v
elektromagtnetickém poli.
Nové - kvantové
pojetí síly: intermediální výměnné částice
V klasické fyzice se každému druhu vzájemného působení
těles přisuzuje příslušné pole - prostor v
němž na částice působí určité síly. V
klasické fyzice je to pole elektrické, magnetické,
gravitační. Velikost působení pole v každém bodě prostoru
se vyjadřuje pomocí intenzity pole (síly
působící na "jednotkovou testovací částici") nebo
pomocí jeho potenciálu (práce spojené s
přenosem částice do daného místa). Změny
("rozruch") v tomto poli se šíří konečnou
rychlostí od místa k místu, což je doprovázeno přenosem
energie, hybnosti a dalších fyzikálních veličin. Z hlediska
klasické fyziky se tyto veličiny, jako je energie a hybnost,
při změnách pole přenášejí spojitě. V kvantové
fyzice se ukazuje, že při změnách (rozruchu) v poli se
fyzikální veličiny přenášejí nespojitě po
určitých "porcích" - kvantech.
Kvantová teorie pole, ve své koncepci druhotného
kvantování, vede k nové představě pole jako souboru
částic - kvant pole. A vzájemné silové působení
(interakce) částic je způsobeno nikoli silou pole, nýbrž
vzájemnou výměnou těchto kvant-částic pole - výměnou
intermediálních částic. Částice neustále
přijímají a vysílají kvanta pole, což vyvolává jejich
vzájemné silové působení. Tato výměnná zprostředkující
(intermediální) kvanta interpretujeme jako částice
- nositele interakcí. Toto představuje nové
pojetí síly a interakce v kvantové teorii pole. Tato
koncepce hraje klíčovou úlohu při interakcích
"elementárních" částic - je
podrobněji rozebíráno v §1.5 "Elementární částice a urychlovače", část "Interakce elementárních částic".
Virtuální či skutečné částice?
Jsou tyto intermediální částice, zprostředkující
interakci, skutečné? Odpověď zní: ano i ne!
Diskutujme si krátce tento problém na elektromagnetickém poli
- kvantové elektrodynamice. Podle ní (jak bylo shora
nastíněno) jsou fotony kvanta elektromagnetického pole
a elektrická síla mezi dvěmi nabitými částicemi je
způsobena neustálou vzájemnou výměnou fotonů.
Kdybychom se však podívali do prostoru mezi dvěma
nepohyblivými náboji, žádný tok letících fotonů bychom
nezaregistrovali. Je to jen model, ony intermediální fotony
jsou zde virtuální! V rámci kvantové
elektrodynamiky se silové působení pouze modeluje
pomocí fotonů: statické pole se uměle rozloží na
superpozici vln (harmonických oscilátorů), ty se kvantují a
vzniklé fotony se označí za kvanta pole, které
zprostředkovávají interakci. Fyzikálně opodstatněné je
spíše tvrzení, že "fotony jsou kvanta
elektromagnetického vlnění", nikoli "kvanta
elektromagnetického pole". Fyzikálně se ve
statickém případě nic nevyzařuje! Skutečné
vyzařování, spojené s přenosem energie a hybnosti - s
proudem fotonů, se děje pouze v dynamickém případě
- při zrychleném pohybu nábojů. Tehdy se virtuální
fotony přemění ve skutečné. Při vzájemných
interakcích (srážkách, rozptylech) částic v mikrosvětě se
vždy jedná o dynamické děje (často za vysokých
energií), při nichž se ve vakuu skryté virtuální
intermediální částice "osvobodí", přemění se ve
skutečné částice a aktivně se účastní interakce.
Pozn.: Zajímavou výjimkou
vyařování virtuálních částic i ve statickém případě je
tzv. Hawkingovo záření kvantové evaporace
černé díry. Vzniká tak, že jedna z obou částic je vtažena
pod horizont černé díry a pohlcena a druhá částice se tak
stává částicí reálnou a může být emitována (je podrobně anylyzováno v §4.7 "Kvantové
vyzařování a termodynamika černých děr" , pasáži "Mechanismus
kvantové evaporace"
monografie "Gravitace, černé díry a fyzika
prostoročasu").
Kvantové
fluktuace polí
Jedním ze základních postulátů kvantové mechaniky je známý
Heisenbergův princip neurčitosti Dx.Dp ł h,
kde h ş h/2p @ 1,05.10-27 g cm3/s je Planckova konstanta. Relace
neučitosti přitom platí nejen mezi
polohou a hybností v kvantové mechanice, ale mezi každými dvěma dynamicky zpřaženými veličinami,
tedy i v kvantové teorii pole. Sledujeme-li např. magnetické pole v
nějaké malé prostorové oblasti charakterizované rozměrem L,
bude tam obsažena energie úměrná B2.L3 a čas potřebný ke změření
pole bude L/c; relace neurčitosti DE.Dt ł h
pak dává (DB)2.L4 ł h.c, neboli DB ł hc/L2. Lze tedy říci, že kvantové fluktuace elektromagnetického pole v
oblasti velikosti L jsou
řádově rovny: DE ~ DB ~ Ö(h.c) / L2 .
Pole
tedy neustále "kmitá" mezi konfiguracemi, jejichž
fluktuační rozmezí je tím větší, čím menší prostorové
oblasti sledujeme. Vliv těchto kvantových fluktuací na pohyb
elektronu kolem atomového jádra (tyto kvantové fluktuace se
"překrývají" přes Broglieovy vlny v Bohrově modelu
atomu - viz pasáž "Bohrův model
atomu",
obr.1.1.6) je
schématicky znázorněn na obrázku :
 |
Schématické znázornění pohybu elektronu kolem atomového jádra. Při podrobnějším pohledu na Keplerovskou trajektorii elektronu by byly vidět drobné chaotické nepravidelnosti způsobené kvantovými fluktuacemi elektrického pole. Střední odchylka od globální trajektorie je rovna nule, avšak střední kvadratická odchylka vede k malému posunu energetické hladiny elektronu. Tento posun byl skutečně změřen jako součást tzv. Lambova-Ruthefordova posunu. |
Při shora zmíněném kvantovém popisu pole -
druhotném kvantování - lze tyto kvantové fluktuace
pole považovat za kvanta - částice. Vakuum se
tak stává vysoce dynamickým prostředím, v
němž neustále vznikají a zanikají virtuální
částice. Tyto částice mají neměřitelně krátkou
dobu trvání, jsou nezachytilelné, říme že jsou virtuální
(....). Kromě toho kvantové fluktuace a virtuální částice
vznikají všude se stejnou hustotou a narážejí na látku ze
všech směrů, takže jejich silové účinky se v
makroskopickém měřítku vyrovnávají a ruší. Za určitých
okolností se však sumární účinky většího množství
těchto částic mohou přece jen drobně projevit i
makroskopicky.
Vedle zmíněného Lambova posunu se
podařilo změřit tzv. Casimírův jev :
Umístíme ve vakuu těsně vedle sebe dvě vodorovné desky
(elektricky nenabité). V mezeře mezi deskami mohou vznikat
kvanta - virtuální částice pouze s krátkými vlnovými
délkami (jejichž celočíselný násobek
je dán šířkou mezery), zatímco v
prostoru mimo desky mohou nabývat libovolných vlnových délek.
Celková hustota částic je tedy v mezeře menší a na desky
převládne tlak částic zvenčí. Desky se tedy k sobě
přitahují silou která je tím větší, čím užší je
mezera mezi deskami.
Dále, pozorovaný dipólový magnetický
moment elektronu je tvořen, kromě základní
elektrodynamické složky, i anomálním magnetickým momentem,
vznikajícím interakcemi elektronu s virtuálními fotony v
kvantové elektrodynamice.
Předpokládáme-li
univerzální platnost kvantového principu neurčitosti, měla
by podobná situace nastávat i v obecné teorii relativity
jakožto fyzice gravitace a prostoročasu: měly by vznikat kvantové
fluktuace geometrie prostoročasu..?. - §B4 "Kvantová
geometrodynamika". Některé
paradoxní interpretace kvantových mikrofluktuací vakua jsou
diskutovány v §B.5, pasáži "Záhada kvantové energie vakua <-> Kosmologická konstanta".
Feynmanovské kvantování dráhových
integrálů
Na začátku naší letmé exkurze do kvantové fyziky jsme se
zmínili, že není nikterak snadné pochopit vnitřní
příčiny kvantového chování mikrosystémů na
základě naší zkušenosti s klasickým chováním makrosvěta.
Jak je např. možné, že v proslulém dvojštěrbinovém
experimentu (obr.1.1.2)
částice může současně projít oběma otvory a pak
interferovat "sama se sebou"?
Feynmanova formulace kvantové teorie se
vyznačuje velmi těsným vztahem ke klasické fyzice *)
vyjádřené pomocí principu nejmenší akce. V klasické fyzice
(mechanice, elektrodynamice, OTR) se mezi daným počátečním x1 a
koncovým x2 stavem vyšetřovaného systému
vždy uskuteční pouze takový pohyb, pro nějž je integrál akce S = x1ňx2L dt extremální. Naproti tomu v
kvantové fyzice se jak známo uskutečnují i takové procesy,
které nevyhovují tomuto principu a jsou podle klasické fyziky
nemožné - např. tunelovy jev.
*) Přechod od klasické
fyziky ke kvantové je zde natolik elegantní a přímočarý,
že se J.A.Wheeler pomocí tohoto přístupu snažil
přesvědčit A.Einsteina, aby zrevidoval svůj odmítavý postoj
ke stochastickým principům kvantové mechaniky. Leč
bezvýsledně: "Nevěřím, že by Bůh hrál se
světem v kostky",
vytrvale namítal Einsten...
Ve Feynmanově přístupu se rovnoprávně
a současně uvažují všechny
trajektorie
vedoucí z počátečního stavu x1 do konečného stavu x2
bez ohledu na to, zda jsou podle klasické fyziky přípustné
nebo nikoliv. Jako kdyby se částice při
cestě mezi oběma stavy pohybovala po každé myšlené
trajektorii současně - jedná se o množinu
všech virtuálních trajektorií
("historií"). Vypočítá-li se pro každou trajektorii
integrál x1ňx2L dt, bude pravděpodobnost
přechodu soustavy z počátečního stavu x1 do koncového stavu x2
dána čtvercem veličiny
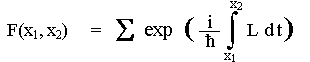 ,
,
získané jako suma vzatá přes všechny trajektorie - součet přes všechny možné "historie". Je evidentní, že největší
příspěvek k této sumě dávají ty trajektorie, které mají
fázový koeficient (i/h)ňLdt téměř stejný (exponenty se
sčítají), zatímco pro trajektorie s velkými rozdíly v (i/h)ňLdt se exponenty v součtu
vzájemně ruší. Nejpravděpodobnější trajektorie
(odpovídající blízkým hodnotám ňLdt)
bude proto klasická trajektorie s extrémním
chováním integrálu akce. Pod trajektorií se zde rozumí
"dráha" v prostoru konfigurací dané soustavy; pokud se jedná o
složitou soustavu popsanou velkým počtem parametrů, bude to
trajektorie v mnoharozměrném prostoru. Feynman ukázal, že
tato formulace je ekvivalentní obvyklému Schrödingerovu a
Heisenbergovu pojetí kvantové mechaniky. Podobně jako u
klasického principu nejmenší akce se v praxi nehledá
bezprostředně extrém integrálu ňLdt, ale odvozují se Lagrangeovy pohybové rovnice, ani při použití Feynmanovy
metody se přímo nepočítá celková suma přes všechny
trajektorie. Feynmanova procedura se spíše používá jako
prostředek pro odvozování a rozpracování kvantových
teorií, jakož i jejich fyzikální interpretace.
..........-doplnit,upravit
Některé
gnoseologické otázky :
Je
kvantová fyzika zásadní překážka poznání a využití
přírody ?
My fyzikové věříme v poznatelnost světa a
naší profesní povinností je pracovat pro co nejdokonalejší
poznání mechanismů a zákonitostí, podle
nichž "funguje" příroda. Z tohoto hlediska jsme
"zděšeni", že nám do fundamentální fyziky
"fušuje" náhodnost, stochastičnost,
statistika, které jsou přece odrazem naší neznalosti
přesných podmínek a stavů ve složitých souborech mnoha
interagujících částic!
Kvantová fyzika je často považována za teorii zásadních
omezení, podle nichž naše pozorování a měření
jsou nevyhnutelně nepřesné, přírodním jevům vládne
náhodnost a měli bychom se vzdát naděje, že by věda
dokázala přesně popsat náš svět. Kvantová mechanika se
často považuje za nepřekonatelnou překážku
na cestě k poznání nejhlubšího mikrosvěta či praktickému
využití mikroskopických jevů (např. další miniaturizace
elektronických obvodů). Již v počátečních obdobích
vývoje kvantové fyziky se ukazovalo, že
korpuskulárně-vlnový dualismus, náhodnost jevů a jejich
superpozice, diskrétnost a především kvantové relace
neurčitosti, nám zásadně brání
chápat a využívat přírodu takovým způsobem a v takové
míře, jak jsme byli zvyklí v klasické fyzice (mechanice,
elektrodynamice, ...). Tento poněkud zavádějící pohled má
své kořeny v době, kdy fyzikové kvantovou mechaniku
vyvíjeli, zdokonalovali a konfrontovali ji s klasickými
teoriemi a filosofickými koncepcemi.
V posledních desítiletích se však stále
častěji prosazuje jiný pohled. Co princip neurčitosti říká
a co neříká? Pouze tvrdí, že ne všechny pozorované
veličiny fyzikálního systému mohou nabývat určité
("ostré") hodnoty ve stejném čase. Ne všechna
kvantová měření podléhají omezení principem neurčitosti.
I když poloha či rychlost jsou neurčité a
"rozmazané", jiné vlastnosti mohou být docela
"ostře" definovány - např. rozmazané elektrony v
atomu vytvářejí dobře definovanou energii daného orbitalu.
Tuto obávanou překážku tak můžeme v některých případech
důmyslně obejít a na kvantové úrovni můžeme využívat
speciální vlastnosti mikrosystémů v nových pokročilých
zařízeních jako jsou lasery, integrované obvody,
nanotechnologie, nové možnosti v informatice a počítačích (viz níže "Kvantová teleportace",
"Kvantové počítače").
........ srov. též diskusi v "Přírodní zákony, modely
a fyzikální teorie".................
Na nejhlubší úrovni je svět diskrétní
nebo spojitý ?
Toto je důležitá gnoseologická
otázka, na kterou se názory fyziků různí. V moderní
terminologii by se tato otázka dala parafrázovat: "Je
fyzický svět v zásadě analogový
či digitální?"
Fyzikální vztah mezi spojitou (kontinuální)
a diskrétní povahou mikrosvěta může být v
zásadě dvojí :
× Diskrétnost je základní: ® sekundárně generuje spojitost
(zdánlivou)
Toto je nejobvyklejší přístup v moderní fyzice, vychází z
atomistiky, termodynamiky a statistické fyziky. Z hledíska
atomové fyziky jsou veškeré látky složeny z diskrétních atomů,
které mají konkrétní celočíselný počet
protonů v jádře a elektronů v obalu. A spektrometrie
záření vydávaného a pohlcovaného atomy ukazuje, že
elektrony v atomu zaujímají diskrétní
energetické hladiny, určované celými čísly.
Na tom je založen Bohrův model atomu (viz níže "Bohrův model atomu"). V souborech velkých
počtů atomů a molekul pak metody statistické
fyziky umožňují odvodit zákony kinetiky plynů a
termodynamiky, které jsou spojité. Avšak
základními "vstupními hodnotami" teorie jsou diskrétní
celá čísla. Spojitost se "vynořuje" ze
zprůměrovaného velkého množství
diskrétních dějů. Voda ve sklenici se jeví jako kontinuální
prostředí, avšak když se na ni podíváme s velkým
zvětšením, uvidíme molekuly a atomy z nichž se skládá.
Tyto atomy mají dále vnitřní strukturu elektronů, protonů a
neutronů.
Na
nejzákladnější úrovni současného poznání je hmota
tvořena fundamentálními leptony a kvarky (§1.5,
část "Standardní model
- jednotné chápání elementárních částic "), které jsou považovány za diskrétní
částice, které lze v zásadě "odpočítávat
jednu po druhé" *).
*) Gnoseologická poznámka:
O úloze celých čísel se v klasické
matematice metaforicky říká, že "Bůh stvořil pouze
celá čísla, všechno ostatní v matematice jsou výmysly lidí".
Pro modelování přírody však matematika zavedla obecnější
množiny, především reálných čísel (viz
§3.1"Geometricko-topologické vlastnosti
prostoročasu", část
"Množiny a zobrazení" ) pro
něž vytvořila rozsáhlý aparát diferenciálního a
integrálního počtu.
× Spojitost je základní:® sekundárně generuje diskrétnost
(opět jen zdánlivou?)
Kvantová fyzika mikrosvěta vychází z korpuskulárně-vlnové
představy. Vlnové rovnice kvantové fyziky (Schrodingerova
rovnice) obsahují jen spojité veličiny.
Názorným příkladem této koncepce je Broglieho vlnové
vysvětlení Bohrových kvantových drah elektronů
kolem jádra atomu - viz níže, obr. AtomBroglie.gif . Zde diskrétnost drah elektronů je formována kontinuitou
vlnových funkcí elektronů - jejich "vlnovou
návazností".
Ve standardním
modelu částic se učí, že výchozími stavebními
kameny hmoty jsou základní diskrétní částice
- leptony (především elektrony) a kvarky. Avšak na
fundamentálnější úrovni, v unitární teorii pole
(§B.1 "Proces
sjednocování ve fyzice"
v knize "Gravitace, černé díry ...."), základním stavebním médiem fyzikálních teorií
je pole - spojitá "fluidní"
substance rozprostřená v prostoru (nejznámějším
příkladem je elektrické a magnetické pole). Z pohledu unitární teorie pole "fundamentální
částice" nejsou fundamentální, ale
jsou složeny ze spojitých polí (a jejich vln
či kvant) - viz níže. Částice jsou
"zhuštěninami" unitárního pole.
Příroda
je patrně opravdové kontinuum, v němž na
žádné úrovni zvětšení nenalezneme žádné již dále
nedělitelné stavební prvky. Fyzikální veličiny obecně nejsou
celá čísla, ale spojitá čísla reálná,
u nichž se s postupným zpřesňováním měření stále
zvyšuje počet míst za desetinnou čárkou. Celá čísla si
zde pak zachovávají jen význam počtu druhů
význačných částic z hlediska typu jejich interakcí (3 druhy neutrin, 6 druhů kvarků),
vyjádření počtu elektronů v atomových obalech, počtu
protonů a neutronů v jádrech, příp. pořadí a počtu
excitovaných stavů.
Je prostor a čas
spojitý nebo diskrétní ?
Ve většině disciplin klasické i kvantové fyziky se prostor a
čas považují za plynulé neomezeně dělitelné kontinuum
- za jakési "jeviště", na jehož pozadí se
odehrávají fyzikální děje, interakce částic a polí. Co
když však spojitost prostoročasu je stejná iluze, jakou byla
do 19.stol. spojitost hmoty? Tak, jak moderní fyzika došla k
poznání o diskrétní kvantové struktuře hmoty, nabízí se
hypotéza, že i prostoročas je kvantován -
skládá se z obrovského, ale spočetného množství
velmi malých již nedělitelných elementárních
"buněk", z jakéhosi "prostoročasového
prachu". Pokud tato hypotetická "kvanta
geometrie" jsou dostatečně malá, např.
velikosti řádu Planckovy délky 10-33cm, jeví se prostoročas jako zcela spojitý, neboť
žádné dosud zkoumané fyzikální procesy nedovedou rozlišit
jemnější vzdálenosti než asi 10-15cm.
Existuje
tedy možnost, že spojité veličiny by v bližším
(zvětšeném) pohledu ve skutečnosti mohly být diskrétní:
mohou ležet na husté mřížce jednotlivých
oddělených bodů, které při nám dostupném pohledu dává iluzi
kontinua. Je to podobné jako pixely na obrazovce
počítače, pozorované při základním zvětšení a při
zoomu.
Pozn.: Stojí za
zajímavost, že v kvantové fyzice byla vyvinuta diskretizovaná
verze kvantových polí - mřížkové pole,
kde kontinuální časoprostor je nahrazen (modelován)
rovnoměrně uspořádanou sadou bodů, jedině v nichž se
stanovují veličiny polí. Je to však jen model usnadňující
kvantové výpočty, neplyne z něho, že je to tak ve
skutečnosti.
Vedle
obecně přijímané koncepce kontinuálního prostoru je
tedy možné alternativně postulovat, či axiomaticky zavést, primární
diskrétnost prostoru: prostor je tvořen jednotlivými
oddělenými "buňkami", jedině v nichž jsou
definovány hodnoty polí (potenciály, intenzity). Tato pole
jsou tím pádem také diskrétní co do prostorové distribuce.
Pokud je prostorová mřížka (matice) dostatečně hustá či
jemná (třebas v rozměrech Planckových délek 10-33cm), jeví se nám
prostor "iluzorně" jako kontinuum. Avšak na
nejhlubších mikroměřítcích by prostor mohl být primárně diskrétní
- "pixelovaný", či "voxelovaný"..?..
Obecná
teorie relativity pojímá gravitační pole jako zakřivený
prostoročas (viz §2.2 "Univerzálnost
- základní vlastnost a klíč k pochopení podstaty gravitace" v knize "Gravitace, černé díry a
fyzika prostoročasu"). Pokud
chceme kvantovat gravitaci, je nutno "kvantovat"
prostoročas. Spojení obecné teorie relativity a kvantové
fyziky tím v samotném časoprostoru odhaluje
(či postuluje) diskrétní strukturu, ať již
fundamentální, nebo indukovanou - viz
§B4 "Kvantová geometrodynamika" a §B5 "Kvantování gravitačního
pole", část "Smyčková
teorie gravitace" v již zmíněné
monografii).
Reflexe
kontinuálních versus diskrétních aspektů přírody je
patrně nezbytná při vytváření unitární teorie
fyziky - teorie všeho - TOE (§B.6 "Sjednocování
fundamentálních interakcí. Supergravitace. Superstruny." monografie "Gravitace,
černé díry a fyzika prostoročasu").
Autorská poznámka:
Já osobně mírně upřednostňuji názor, že fundamentální
je spojitost (dokonce snad kauzální?), která indukuje
zdánlivou diskrétnost (a snad i kvantovou
stochastičnost)..?.. Avšak i koncepce diskrétní superhusté
prostoročasové mřížky by snad mohla být nosnou myšlenkou
pro pochopení mikrosvěta..?..
Záporný čas v mikrosvětě ? -
Asi ne ..!..
Při průchodu elektromagnetického
záření - fotonů vhodné energie - látkovým prostředím
dochází k jejich absorpci atomy, které se tím dočasně excitují
na vyšší energetické stavy. Následně dochází k deexcitaci
při níž vyzařují fotony spektrálních energií (je
podrobněji diskutováno níže v pasáži "Excitace a
spektra záření atomů").
Za normálních okolností jsou tyto sekundární fotony časově
následné, s určitým (většinou
velmi malým) časovým zpožděním.
Při vysoce citlivých experimentech s velmi krátkými
(pikosekundovými) laserovými impulsy se však někdy
překvapivě ukazuje, jakoby některé sekundární fotony
opustily materiál nepatrně dříve,
než do něj primární fotony vstoupily! Jako kdyby mezi procesm
excitace a deexcitace atomů uplynul "záporný
čas"..?..
Vyskytly se spekulace o existenci skutečného
"negativního času", který by se dal využít k
cestování časem do minulosti ("Cestování
časem - fantazie nebo fyzikální realita?")... Reálné vysvětlení
těchto paradoxních pozorování však toto odmítá jako
zavádějící a obrací se ke dvěma fyzikálním okolnostem :
1. Fázový posun na dráze fotonů, který
může "simulovat" drobné časové posuny mezi emisí
a detekcí fotonů. 2. Kvantové relace
neurčitosti, kterým podléhají i fotony a atomy, které jsou
"rozmazané" v prostoru i v čase. Takže v kvantové
fyzice efektivně i čas může drobně fluktuovat kladným i
záporným směrem...
Je svět poznatelný ?
Tato základní gnoseologická
otázka se často diskutuje z nejrůznějších pohledů
filosofických. Z přírodovědného hlediska
poznatelnost našeho světa můžeme reflektovat v zásadě na
třech úrovních :
1.
Fenomenologická
poznatelnost
Zkoumání konkrétního průběhu jednotlivých přírodních
dějů je základem přírodovědného poznání. Přesnost
tohoto poznání je dána úrovní (rozlišovací schopnosti)
fyzikální přístrojové techniky, optických pozorovacích
systémů, chemicko-analytických metod. Principiální
omezení ve fenomenologickém poznávání nám v
mikrosvětě kladou kvantové relace neurčitosti
(viz např. část "Kvantová
fyzika" v §1.1), v makro- a megasvětě pak horizonty
událostí relativistické astrofyziky (§3.3 "Cauchyova úloha,
příčinnost a horizonty"
v monografii "Gravitace, černé díry....").
2.
Poznání
vnitřních příčin, mechanismů, zákonitostí
Toto je hlavní náplní pokročilého vědeckého zkoumání. Z
podrobné analýzy průběhu přírodních dějů za různých
podmínek a srovnáváním z jinými ději se formulují obecné přírodní
zákony, pokud možno s univerzální platností
pro širší třídu jevů. Toto umožňuje porozumět
fungování přírody (je
diskutováno v části "Přírodní
zákony, modely a fyzikální teorie" §1.1 v již zmíněné knize "Gravitace,
černé díry...").
3.
Absolutní
deterministická poznatelnost
Maximalistický požadavek úplné poznatelnosti
světa by vyžadoval, abychom u všech elementárních částic,
atomů, molekul a dalších struktur dokázali předpovědět
jejich přesné prostorové polohy ve všech
časových okamžicích, jakož i předpovědět přesné hodnoty
polí (potenciálů, intenzit) ve všech místech
prostoru. Naše dosavadní poznání ukazuje, že toto není
možné! Kromě technické nerealizovatelnosti tomu na
mikroskopické úrovni brání kvantové relace
neurčitosti, na všech úrovních pak zvláštní
nepravidelnosti v chování souborů částic, zvané "deterministický
chaos", generující náhodu - je
podrobněji diskutováno v části "Determinismus-náhoda-chaos
?" §3.3 v knize "Gravitace, černé díry a fyzika prostoročasu". Dále, pokud je prostor spojitý
(viz diskusi výše "Je
prostor a čas spojitý nebo diskrétní?"), nekonečná a dokonce nespočetná
množina jeho bodů by vyžadovala nekonečné množství
dat pro každý, byť sebemenší okrsek zkoumaného systému!
Vyvozovat z negativního vyznění úrovně 3.
kategorické tvrzení o nepoznatelnosti světa
však není opodstatněné a může být zavádějící *)! Svět
je totiž v zásadě poznatelný v tom smyslu,
že rozumíme mechanismům jeho fungování, na
jejichž základě dovedeme často dlouhodobě a s velkou
přesností předpovídat chování mnohých důležitých
systémů v přírodě a vesmíru. Např. pohyby planet ve
Sluneční soustavě dovedou astronomové na základě
Newtonových a Keplerových zákonů (gravitace a mechaniky) s
vysokou přesností předpovídat na mnoho staletí dopředu. V
horizontu miliónů až miliard let však drobné gravitační
poruchy nakonec vyústí v chaotické odchylky, které výrazně
změní pohyby planet (některé z nich
mohou i ze soustavy uniknout...). Není
tedy výstižné říkat, že "svět je nepoznatelný",
ale že "poznatelnost světa má svá omezení".
*) Takové ostré tvrzení, že
"svět je nepoznatelný", by
mohlo vyvolávat skepsi, nihilismus, agnosticismus. Nahrávalo by
též různým "alternativcům" a šarlatánům,
kteří bagatelizují impozantní úspěchy seriózního
vědeckého poznání a tvrdí, že jen oni, díky svým
"zázračným schopnostem", mají dar "pravého
poznání" a mohou ovládat svět (či spíše některé
důvěřivé lidi...).
Některé neobvyklé a
paradoxní důsledky kvantové fyziky
Kvantový tunelový jev
Jestliže se částice pohybuje v určitém silovém poli, je
při pohybu podle klasické fyziky v každém bodě trajektorie
splněn zákon zachování energie - součtu
kinetické energie částice a její potenciální energie v
daném poli. Zajímavým případem pohybu částice je pohyb v
silovém poli, jehož potenciál má tvar potenciálové
bariéry - v nejjednosušším případě pohybu ve
směru osy X na částici působí takové síly, že její
potenciální energie Ep je všude nulová, s výjimkou oblasti x1<x<x2, kde má hodnotu Ep=Vo. Pokud kinetická
energie částice Ekin je menší než výška Vo potenciálové bariéry, měla by se podle klasické
fyziky částice při pohybu od místa bariéry odrazit a
pohybovat se zpět proti původnímu směru pohybu - částice
není nikdy schopna překonat potenciálovou bariéru.
Potenciálovou bariéru může částice překonat pouze když
má dostatečně velkou kinetickou energii Ekin>Vo.
V kvantové mechanice, kde je částice popsána vlnovou
funkcí (podle korpuskulárně-vlnového dualismu je
Broglieho vlnou), však existuje nenulová pravděpodobnost, že
vlna "prosákne" bariérou a částice se může
najednou ocitnout na druhé straně bariéry. Vlny se totiž, na
rozdíl od klasických částic, mohou díky ohybu
dostat i za překážku a pak pokračovat v dalším pohybu
prostorem. Rozbor vlnové funkce pomocí Schrödongerovy rovnice
ukazuje, že rovinná vlna dopadající na stěnu bariéry se od
ní částečně odráží (a interferuje s původní vlnou) a
částečně proniká dovnitř bariéry. Je-li
šířka d=x2-x1 bariéry dostatečně
malá ve srovnání s hloubkou proniknutí vlny, dosáhne
Broglieova vlna druhé stěny bariéry, kde potenciál náhle
klesá - vlna vstupuje do volného prostoru a pokračuje ve svém
pohybu směrem od bariéry jako rovinná vlna, s nižší
amplitudou (vyjadřující pravděpodobnost
průchodu částice na druhou stranu bariéry). Částice prošla potenciálovou
bariérou i tehdy, když energie částice je podle klasické
fyziky nedostačující na překonání bariéry!

Symbolické znázornění kvantového tunelového jevu.
Vlevo: Kulička kutálející se s kinetickou energií Ekin proti vyvýšené
terénní vlně (kopci - gravitační potenciálové bariéře
výšky Vo)
ji může překonat jen tehdy, když má dostatečnou energii Ekin>Vo. Uprostřed:
Pokud je v terénní překážce proražen tunel, může ji
těleso překonat i při podstatně nižší energii než je
potenciálová výška Vo. Vpravo: Zjednodušené znázornění
pravoúhlé potenciálové bariéry výšky Vo, kterou mohou
částice (~vlny) s určitou pravděpodobností projít i při
nižší kinetické energii než je Vo - jako kdyby přes bariéu vedly "skryté
tunely".
Z energetického hlediska se
popsaný fenomén dá vysvětlit pomocí kvantové relace
neurčitosti DE . Dt ł h mezi energií a časem (bylo
rozebíráno výše). Hodnota okamžité
energie částice v kratičkých časových okamžicích
fluktuuje kolem své střední velikosti, nahoru
i dolů. V okamžiku, kdy částice dorazí k potenciálové
bariéře, může být ("shodou okolností") na
krátký čas její energie momentálně zvýšená,
což jí umožní bariéru překonat. Během aktu vlastního
průniku, v rámci relace neurčitosti, nemusí platit zákon
zachování energie. Čím kratší je okamžik fluktuace Dt, tím větší je
její možný rozsah DE. Pokud se částice nestihne dostat na druhou stranu
bariéry za tuto dobu trvání dostatečně velké fluktuace,
vrátí se zpátky - odrazí se; to se samozřejmě stane i v
případě, že v okamžiku dosažení bariéry je fluktuace
energie negativní. Čím je potenciálová bariéra širší a
vyšší, tím menší je pravděpodobnost úspěšného
proniknutí částice; většina částic proniká do bariéry
jen zčásti a od potenciálového valu se nakonec odráží. U
dostatečně úzké bariéry je větší pravděpodobnost, že v
důsledku dostatečně vysoké krátkodobé fluktuace energie ji
částice stihne úspěšně překonat.
Tento efekt, kdy částice prochází
potenciálovou bariérou vyšší než energie částice, se
nazývá tunelový jev - částice, která nemá
dostatečnou kinetickou energii (a nemůže tudíž
"proletět" nad potenciálovou bariérou), může
přesto s určitou pravděpodobností proniknout bariérou, jako
kdyby v ní byl vyvrtán nějaký skrytý "tunel".
Částice se na druhou stranu bariéry jakoby "protunelovala".
Tunelový jev má pravděpodobnostní charakter. Projevuje se
buď u velkého počtu dopadajících částic, z nichž
některým se podaří "protunelovat", nebo jednotlivá
částice musí mít možnost vykonat nejprve řadu
"neúspěšných pokusů", než se jí
"podaří" uvolnit se z vazby v jádře (např. alfa-radioaktivita) nebo v
materiálu (např. termoemise).
Pravděpodobnost w kvantového tunelového
průchodu částice s kinetickou energií Ekin potenciálovou bariérou výšky Vo (>Ekin) a šířky d je přibližně rovna
w » exp(-2d.Ö[2m.(Vo-Ekin)/h2]) .
Tato pravděpodobnost exponenciálně klesá s šířkou d
potenciálové bariéry.
Jedním ze základních parametrů, kterým
charakterizujeme fyzikální systémy je jejich energetický
obsah. Pokud má nějaký systém k dispozici stav s nižší
energií než je ta aktuální, jeho dynamika (působící síly) má snahu
dostat ho do tohoto nižšího energetického stavu. Často však
vznikají situace složitějších závislostí potenciálu, kdy
dosažení tohoto nižšího energetického stavu nejprve
vyžaduje lokální vystoupení do vyššího energetického
stavu - je v cestě potenciálová bariéra, kterou je nutno
"přelézt". V klasické fyzice je taková překážka
nepřekonatelná a k dosažení nižšího stavu nedojde,
vyšší stav je metastabilní. Musíme nejdříve
"investovat" určitou energii, abychom
překonali energetickou bariéru a teprve pak můžeme "profitovat"
z uvolněné energie. Kvantový systém umožňuje překonat tuto
bariéru i bez dodání vnější energie. To, co je v klasické
fyzice nemožné, je v kvantové fyzice jen méně
pravděpodobné... Při tunelování bariérou systém nikdy
není možné pozorovat v přechodovém stavu s vyšší energií
než měl na počátku, ale jen před tunelováním s danou
počáteční energií a po tunelování ve výsledném stavu s
nižší energií a s uvolněnou energií v určité jiné formě
(jako je záření, teplo, ...). Pro celkovou energetickou bilanci přesně platí
zákon zachování!
Tunelový jev, který je typicky
kvantově-mechanický efekt spojený s vlnovými vlastnostmi
částic, se výrazně uplatňuje v řadě jevů mikrosvěta - v
atomech i atomových jádrech (např. v radioaktivitě
alfa, jaderných reakcích -
především v termonukleární fúzi), v elektrických jevech ve vodičích a
polovodičích. V elektrickém poli může docházet k emisi
elektronů z kovů (termoemise, fotoemise) i tehdy, když
kinetická energie elektronů je nižší než příslušná výstupní
práce; na kvantové tunelové emisi elektronů z povrchu
vodivých látek je založen tunelový rastrovací
mikroskop. Řada procesů na mikroskopické úrovni
může díky tunelovému efektu probíhat i při podstatně nižších
energiích, než jaké by byly nutné podle klasické
fyziky. Bez něho bychom neměli šanci využívat přírodní
energii - ani šanci na život!
Schrödingerova
kočka - chybná
interpretace kvantové fyziky ?
Je to poněkud morbidní *) a absurdní myšlenkový experiment,
který rakouský fyzik E.Schrödinger v r.1935 zformuloval, aby
ukázal paradoxní vlastnost superpozice stavů v
kvantové fyzice. Víme, že když v mikrosvětě je nějaký
stochastický jev pozorován - změřen, ovlivňuje to jeho stav.
Jestliže máme nějakou částici, např. elektron, změřením
jeho polohy nebo rychlosti dostaneme určitý výsledek. Avšak
při samotném změření jsme trochu narušili jeho polohu a
rychlost, takže vyvstává otázka, jak to vypadalo předtím
než jsme to změřili a narušili? Kvantová mechanika nabízí
interpretaci, že když změříme určitou vlastnost elektronu
(polohu nebo rychlost), dostaneme určitý výsledek, ale než
jsme to změřili, existoval tento elektron ve všech možných
stavech najednou. A teprve akt změření je to, co ho donutí
přijmout jeden určitý stav. Schrödinger se tímto
"kočičím experimentem" snažil poukázat na
absurdnost této interpretace, která však později byla v
kvantové fyzice většinou akceptována...
*) Virtuální morbidita tohoto
experimentu byla za několik let bohužel vystřídána
skutečnou morbiditou, které se dopouštěli jeho němečtí
soukmenovci, kteří tentýž kyanovodík používali k
vraždění tisíců lidí v koncentračních táborech..!..
Samotný Schrödinger byl ovšem rozhodným odpůrcem
hitlerovského fašismu.
V hermeticky uzavřené neprůhledné krabici jsou umístěny
následující objekty :
1. Živá kočka; 2. Uzavřená
baňka s jedovatým plynem - kyanovodíkem (v
první verzi se jednalo o pušku namířenou na kočku);
3. Vzorek radioaktivního
materiálu obsahující jeden atom radionuklidu s poločasem
rozpadu 1 hodina;
4. Detektor záření elektronicky
spojený s mechanismem schopným otevřít baňku. Když se
radioaktivní atom rozpadne, detekční přístroj to
zaregistruje, elektrické zařízení uvnitř krabice odzátkuje
baňku s jedovatým plynem a kočka zemře.
Schmatické znázornění myšlenkového pokusu
"Schrödingerovy kočky".
Rozpad radioaktivního atomu je stochastický
kvantový jev - nedovedeme předpovědět čas kdy se jádro
rozpadne, jen příslušnou pravděpodobnost; po jedné
hodině je zhruba 50% pravděpodobnost, že se nuklid rozpadl.
Podle interpretace kvantové mechaniky se radionuklid, který
není pozorován, nachází v superpozici rozpadlého a
nerozpadlého jádra, jako by byl v obou stavech zároveň.
Takže i celá navazující soustava v krabici by se měla
nacházet v superpozici stavů: [rozpadlý
radionuklid - mrtvá kočka] a [nerozpadlý
nuklid - živá kočka]. Pokud však otevřeme
krabici, uvidíme samozřejmě jen jeden z těchto stavů.
Paradox spočívá v tom, že v interakci s
vhodným kvantovým systémem (radionuklidem) se kočka může
dostat do stavu, kdy je jakoby živá i mrtvá současně. Podle
kvantové mechaniky je systém v krabici popsán vlnovou funkcí,
která obsahuje kombinaci (superpozici) těchto dvou možných
vzájemně se vylučujících stavů - tedy v každém časovém
okamžiku je kočka živá i mrtvá zároveň. Až když
provedeme pozorování (otevřením krabice), v tu chvíli
donutíme systém aby přijal jednu nebo druhou možnost. Takže
když otevřeme víko krabice, vnější pozorování rozhodne,
zda kočka opravdu žije nebo ne. Myšlený experiment poukazuje
na nedokonalost (neúplnost, nekompletnost) této interpretace
kvantové mechaniky při komplexním chápání přírody, při
přechodu mezi mikro- a makrosvětem.
Tento myšlený experiment byl populární zejména v období
budování koncepcí kvantové mechaniky, kdy sehrál určitou
heuristickou úlohu. Z dnešního pohledu již není
příliš přesvědčivý... Spíše než rozpornost
fyzikální skutečnosti vyjadřuje paradoxnost jejího
formálního popisu. Je to chybná, často
se vyskytující interpretace kvantové mechaniky (srov. též shora uvedenou diskusi o Kodaňské
interpretaci kvantové mechaniky "Vlnové
funkce. Interpretace kvantové fyziky."
a jejich problémech "Superpozice
různých stavů a kolaps vlnové funkce: někdy chybná
interpretace kvantové fyziky?").
Ve
skutečnosti částice před pozorováním-měřením není
ve všech možných stavech najednou - je jen v jednom
stavu, který neznáme. My před měřením
můžeme stanovit jen pravděpodobnost, v jakém stavu
by mohla být. A po měření pak známe konkrétní stav jistě.
Poznámka: Možné
řešení tohoto paradoxu se někdy uvažuje z hlediska hypotézy
nekonečného množství paralelních světů, v
nichž se realizují všechny možnosti (je diskutováno v §5.7
"Antropický princip a existence více vesmírů", pasáž "Koncepce více
vesmírů"). V jednom vesmíru je kočka
mrtvá, v "sousedním" vesmíru experiment přežila...
Kvantová provázanost a teleportace.
Kvantové počítače.
Zajímavým a pro klasickou fyziku zcela překvapivým důsledkem
principiální nelokálnosti kvantového popisu
částic pomocí vlnových funkcí je jev zvaný kvantová
provázanost. Spočívá v představě, že dvě
částice, jejichž kvantový stav je "provázán"
původně společnou vlnovou funkcí, zůstávají v jistém
smyslu spojeny i nadále jakýmsi
"neviditelným poutem", a to i na libovolně velkou
vzdálenost. Změní-li se stav jedné z provázaných částic,
dojde i ke změně stavu druhé částice, a to
"okamžitě" - nastává jakási "teleportace"
informace, podle některých názorů "nadsvětelnou
rychlostí"..?.. (bude
diskutováno níže).
Jak bylo výše uvedeno, evoluce kvantového
systému je popsána vlnovou funkcí. Je to (myšlená) vlna šířící se
prostorem, přičemž objekt ("částice") se
"vyskytuje", v nelokálním smyslu, všude na čele
této vlny. Při interakci objektu s jiným kvantovým objektem
či s měřícím přístrojem dochází ke "kolapsu vlnové
funkce", přičemž se objekt dočasně lokalizuje
a může být popsán částicově. Kolaps vlnové funkce přitom
probíhá nelokálně - vlnová funkce, podle
této interpretace, vymizí náhle z celého prostoru..?.. Je to
jen teoretická-hypotetická představa...
Podle obvyklé tzv. Kodaňské interpretace
kvantové mechaniky se vyšetřovaný systém skládá ze
samotných kvantovaných objektů a z klasických měřících
přístrojů či pozorovatelů. Kolaps vlnové funkce lokalizuje
informaci, kterou pozorovatel získal měřením.
Máme-li dvojici prostorově
oddělených kvantových subsystémů, které tvoří součást
jediného systému, jsou tyto podsystémy vzájemně
vázány přes společnou původní vlnovou funkci.
Změření (interakce) jednoho takto vázaného subsystému
"nutí" druhý vázaný subsystém okamžitě přejít
do odpovídajícího (komplementárního) stavu, bez ohledu na
prostoročasovou vzdálenost. Tento jev se označuje jako EPR-nelokalita
(Einsteinova-Podolského-Rosenova), či jako EPR-paradox.
A.Einstein se spolupracovníky B.Podolským a
N.Rosenem zformulovali níže nastíněný myšlenkový
experiment aby ukázali vnitřní rozpornost a neúplnost
kvantové fyziky. .Jeví se paradoxní, že bez přítomnosti
výměnných (zprostředkujících) částic či polí lze
okamžitě ovlivňovat částici, která je třebas na opačném
konci vesmíru - jakési "strašidelné
působení na dálku"! Podle speciální
teorie relativity lze očekávat, že v kauzálním kontaktu
mohou být jen místa, mezi nimiž je prostoročasové spojení
omezené rychlostí světla. Kvantová mechanika však svou
nelokálností vlnových funkcí tento kauzální
požadavek relativistické fyziky může v určitém
smyslu dočasně porušovat. Nyní se kvantové
provázání již za paradoxní většinou nepovažuje.
Provedením měření u jedné částice se ke druhé částici
nepřenáší žádná hmota ani energie. A co se týče
informace, oba pozorovatelé pro konfrontaci naměřených
výsledků musí použít "klasickou" komunikaci
pomocí signálu s podsvětelnou rychlostí; tím je zajištěna
STR kauzalita obou měření (viz též
níže komentář k obr.1.1.3).
Vzájemné
nelokální provázání či "propletení"
kvantových stavů se anglicky označuje jako entanglement.
Je to kvantově korelovaný stav systému dvou či více
částic, v němž nelze změřit stav jedné částice, aniž
bychom ovlivnili druhou (a tudíž nemá
smysl mluvit o stavech jednotlivých částic). Obě částice mají společnou nelokální
vlnovou funkci.
Lze to názorně ilustrovat na příkladu
částice původně v klidu, s nulovým momentem hybnosti, která
se rozpadne na dvě od sebe letící stejné částice, každou
se spinem 1/2. Zákon zachování celkového momentu hybnosti
implikuje, že pokud naměříme u jedné částice projekci
spinu do určité osy 1/2, musí mít druhá částice projekci
spinu do téže osy -1/2 (a naopak). Pokd tedy provedeme
měření spinu na jedné částici, okamžitě se
dozvíme hodnotu spinu u druhé částice, ať je jakkoli daleko.
Podle některých názorů, jako by se tato informace šířila
okamžitě, v rozporu se speciální teorií relativity *) ! Z
kvantově-mechanického nelokálního pohledu při měření na
jedné částici "zkolabuje" společná vlnová funkce
v celém prostoru, což se projeví na stavu druhé částice.
Skutečné ověření a rekonstrukci změřeného kvantového
stavu druhé částice je však možné pouze klasickým
komunikačním kanálem s podsvětelnou rychlostí!
*) V tom spočívá často
uváděný mylný názor o nadsvětelné
rychlosti kvantové teleportace. Pokud víme, že obě částice
jsou kvantově provázány a mají opačně orientovaný spin,
změření spinu jedné částice samozřejmě implikuje opačný
spin druhé částice, bez nurnosti jejího měření a
teleportace informace. A když to nevíme, obecně je nutno
informace o stavu částic přenášet komunikačním signálem s
podsvětelnou či světelnou rychlostí.
Dalším
typickým příkladem "entanglovaných" částic je dvojice
fotonů vznikajících současně při určitém
kvantovém procesu. Může to být dvojice fotonů emitovaných z
atomu po jeho excitaci, jejichž polarizace může být
korelována (v nejjdenodušším případě
na opačnou, vzájemně kolmou). Pokud na
jednom fotonu naměříme polarizaci např. ve směru vodorobné
osy X, polarizace druhého fotonu bude ve směru Y. Může k tomu
docházet i u záření g vznikající při anihilaci částice a antičástice
(viz §1.2 a 1.5). Kvantově propletené fotony též vznikají v
nelineárních optických krystalech při dopadu koherentního
monochromatického záření z laseru, kdy některé dopadající
fotony se při interakci "rozdvojí" na dva vázané
fotony s nižší energií, jejichž polarizace jsou vzájemně
komplementární.
Kvantová
teleportace
Výraz "teleportace" (řec. tele=vzdálenost, lat. portare=nést,
přenést; tedy přenesení, přemístění na dálku), vyskytující se často ve vědecko-fantastické
literatuře, obecně označuje proces, kdy daný předmět (ve sci-fi dokonce i osoba) na
původním místě zmizí a objeví se na jiném místě
(ve sci-fi třebas na druhém konci
vesmíru, okamžitě či nadsvětelnou rychlostí). V sofistikovanějším provedení se jedná o nepřímé
přemísťování: objekt je na jednom místě rozebrán a
analyzován, získané kompletní informace o jeho
stavbě se přenesou na jiné vzdálené místo, kde se pak
pomocí těchto informací vytvoří (rekonstruuje) přesná
kopie původního objektu. Tato kopie se přitom nevytvoří
z původní hmoty, ale z částic stejného druhu (např. atomů)
na novém místě, které jsou sestaveny do stejné struktury,
jakou měl původní objekt - nejedná se o fyzický přenos
předmětů - jejich hmoty (látky), ale o přenos
informace. A rozhodně neprobíhá nekonečnou či
nadsvětelnou rychlostí!
Kvantově provázaných (entanglovaných) částic
lze v principu využít k tzv. kvantové teleportaci
informace o stavu další částice, která vstoupí do interakce
s jednou z nich. V r.1993 navrhl Ch.Bennet následující
nepřímý způsob (obr.1.1.3) :
Obr.1.1.3. Zjednodušený princip
uspořádání pro kvantovou teleportaci.
Mějme pozorovatele O1 (laboratoř odesílatele) a pozorovatele O2 (laboratoř příjemce). V
místě pozorovatele O1 vytvoříme dvojici entanglovaných částic
A a B tak, že částice A zůstává v místě O1 a částice B je vyslána k
pozorovateli O2.
Pozorovatel O1 pak
provede interakci částice A s třetí částicí C nesoucí
informaci (stav) jež má být teleportována; změří
výsledné stavy částice A a C po interakci. Původní stav
částice C se přitom vymaže, ale díky entanglementu se tato
informace objeví (v zakódované formě) na vzdálené částici
B, jejíž stav B´ změří pozorovatel O2. K tomu, aby pozorovatel O2 správně stanovil původní stav částice C který
byl v místě O1,
musí se pozorovatel O1 spojit s pozorovatelem O2 pomocí klasického (nekvantového, kauzálního)
komunikačního kanálu (např. elektromagnetickým signálem) a
sdělit mu, jaký výsledek stavů částice A a C po interakci
naměřil. Pozorovatel O2 pak zkonfrontuje výsledek svého měření stavu
částice B s údaji sdělenými pozorovatelem O1 (pomocí nich provede
dekódování svého výsledku metodou lineárních transformací
typu rotací ve vektorové bázi ...), přičemž konečným
výsledkem je stanovení (rekonstrukce) původního stavu
částice C v místě O1 - odpovídá to teleportaci této
informace.
Pro uskutečnění kvantové teleportace je tedy
zapotřebí jak nelokální "EPR" kanál
entanglovaných částic, tak normální (kauzální)
komunikační kanál. Jen tak lze teleportovanou informaci
dekódovat. Právě tato nutnost klasické komunikace efektivně
znemožňuje posílat informace nadsvětelnou rychlostí.
Kvantová teleportace tedy neporušuje principy kauzality
speciální teorie relativity - EPR již není paradoxem.
Proces kvantové teleportace v jeho dosavadním
chápání může fungovat jen v rámci elementárních částic
a nelze jej použít pro teleportaci makroskopických objektů.
Není znám žádný způsob, jak by soustava kvantově
vázaných stavů mohla cíleným způsobem interagovat s
makroskopickým objektem. Navíc tato metoda přenáší jen
hodnotu jedné pozorovatelné veličiny, nikoli kompletní
kvantový stav.
Kvantová teleportace polarizačního stavu UV
fotonů byla poprve experimentálně uskutečněna v r.1997 v
laboratoři kvantové optiky a spektrometrie v Innsbrucku.
Později byla kvantová teleportace provedena na excitovaných
stavech iontů vápníku 40Ca+ (v téže laboratoři v
Innsbrucku) a berylia 9Be+ (v Národním institutu pro
standardy a techologie v USA). V r.2017 se
podařilo teleportovat fotony mezi pozemní stanicí a čínskou
družicí Micius na vzdálenost 1400 kilometrů.
Kvantová
elektronika, kvantové počítače
Důležitou kvantovou vlastností částic, elektronů, protonů
i celých atomů je spin - vlastní vnitřní
rotační moment hybnosti částice. Částice s nenulovým
spinem se mohou chovat jako magnetické dipóly, které
reagují na vnější magnetické pole. Spin elektronu je
orientován dvěma opačnými směry (projekce
spinu), které se označují jako stavy
mířící nahoru |á> a dolů |â>. Při průletu takové částice vhodně
konfigurovaným (nehomogenním) magnetickým polem se částice se spinem |á> vychylí
na jednu stranu, zatímco částice se spinem |â> se
vychýlí na opačnou stranu. Dopadají proto do různých
míst elektronických detektorů. Na tomto principu se
rozvíjí tzv. spintronika - elektronika, která
kromě náboje elektronů využívá i orientace jejich spinu.
Digitální aplikace principů této kvantové elektroniky vede
ke kvantovým počítačům.
Na
tyto pozoruhodné kvantové vlastnosti se proto v poslední době
"vrhli" odborníci v oblasti informatiky,
kybernetiky a počítačů, kteří je
přeformulovali do své digitální terminologie a spolu s fyziky
začali pracovat na možnostech praktických aplikací
v této oblasti. V současné (již
klasické) digitální a počítačové
technice je základní jednotkou informace "bit"
- elektronický signál jehož stav nabývá dvou hodnot (je digitální), které se
vyjadřují jako "0" nebo "1".
Bývá realizován dvěma normalizovanými dobře odlišitelnými
hodnotami napětí v hradlovém obvodu. Skupiny
kombinací těchto bitů (byte -
"bajty", skupiny 8 bitů) pak ve dvojkové
soustavě vyjadřují kódy a číselné hodnoty všech dat.
V kvantové informatice se jako základní
jednotka zavádí tzv. kvantový bit neboli qubit
(quantum bit) jakožto kvantová verze bitu - digitální jednotky
informace. Zatímco klasický bit je vždy buď
ve stavu |0> nebo |1>, qubit během procesu nese i
libvolné hodnoty mezi 0 a 1 - zahrnuje navíc i
všechny superpozice pravděpodobností těchto stavů.
Ve vlnové funkci je paralelně nesena informace o všech
koeficientech superpozice.
Stav qubitu |q> se zapisuje jako: |q>
= A.|0> + B.|1>,
kde A a B jsou komplexní
koeficienty pravděpodobnosti stavů |0> a |1>, pro které
platí A2+B2 = 1.
Komplexní superpoziční stav "mezi 0 a
1" je implicitně obsažen pouze ve volném stavu, bez
jakékoli interakce. Konkrétní explicitní hodnotu |0> nebo
|1> nabývá qubit teprve v okamžiku měření
(interakce). Při interakci (když se na
něj "podíváme", detekujeme jej, dekódujeme) se stav qubitu "překlopí" - v kvantové
terminologii "zkolabuje" - na jednu či druhou
stranu, podle toho která je v tom okamžiku
nejpravděpodobnější.
Kvantové
počítače využívají především tři specifické jevy z
kvantového mikrosvěta: kvantovou superpozici
stavů, kvantovou provázanost a interferenci
(konstruktivní či destruktivní) kvantových stavů. Kvantový počítač je založen na
třech základních principech :
1. Technická
realizace qubitů 2. Kvantové
provázání (entaglement) qubitů 3. Detekce a
dekódování kvantových stavů (logické operace s qubity)
Ad 1:
Pro technickou realizaci qubitů lze
využít vhodných dvouúrovňových kvantově-mechanických
mikrosystémů (fotonů, elektronů,
atomů). Zatím jsou odzkoušené čtyři
způsoby pro realizaci qubitů :
¨
Využití polarizace fotonů; ¨ Využití
spinu částic, především
elektronů; ¨ Využití excitovaných atomů, především
atomů vodíku;
¨
Využití supravodivých vodičů,
uspořádaných do tzv. Josephsonových přechodů (jsou popsány v §2.5, pasáž "Mikrokalorimetrické detektory", odstavec "SQUID").
Použít by se mohlo i několik dalších
speciálních kvantových jevů (.....), které ale zatím nebyly
realizovány.
Ad 2:
Kvantové provázání (entaglement) qubitů
lze provádět vzájemnou interakcí částic, atomů či iontů.
Provázané kvantové stavy se často realizují pomocí
laserového impusu.
Pokud se podaří kvantově provázat N qubitů, je počet
superpozičních koeficientů 2N. Operace s těmito provázanými qubity jsou paralelní
(probíhá se všemi koeficienty
superpozice), což dává potenciál vysoké
výkonnosti elektronického ukládání, přenosu a
analýzy informací.
Ad 3:
Pro rozpoznání a dekódování
kvantových stavů qubitů a pro logické operace s nimi se
používají metody závislé na druhu použitých qubitů. Pro polarizované
fotony jsou to metody optoelektronické.
Měření roviny polarizace můžeme provádět tak, že do cesty
fotonu postavíme polarizační filtr, kterým projdou jen fotony
s určitou rovinou polarizace (stav |1>), zatímco fotony
polarizované kolmo na rovinu filtru neprojdou (stav |0>).
Fotony polarizované v jiných rovinách se budou chovat jako
qubit v superponovaném stavu - podle úhlu natočení polarizace
se bude měnit amplituda pravděpodobnost, že foton projde či
neprojde polarizačním filtrem. Pro orientace spinů
se používají metody magnetoelektronické.
Perspektivy
kvantových počítačů ?
Aplikace zákonitostí kvantových vlastností v informatice a
počítačové technice slibují lákavé možnosti kvantových
počítačů, které by některé výpočetní úkoly
mohly být schopné řešit mnohonásobně rychleji než
klasické počítače. Často uváděná, avšak ve skutečnosti
okrajová, je možnost dokonalé kvantové kryptografie (ochrana přenášených dat pomocí kvantových
klíčů).
Problémem je sestavit kvantové počítače s
dostatečně velkým počtem qubitů. Velké soubory částic se
již přestávají chovat podle zákonů kvantové fyziky a
začínají se řídit zákony klasické mechaniky a
elektrodynamiky. Zkoumají se možnosti vytvářet tzv. modulární
kvantové systémy: konstrukce mnoha malých kvantových
procesorů a jejich propojení malým počtem uzlových quibitů,
které by nenarušilo jejich kvantové vlastnosti (vlastní moduly zůstávají navzájem relativně
izolované). V "high-tech"
laboratořích mikroelektroniky se vyvíjejí kvantové
čipy, ve kterých jsou generovány a nalyzovány páry
entanglovaných iontů (v iontových
pastech) nebo entanglovaných fotonů (v optických krystalech či mikroprstencových
rezonátorech). Ty by se mohly stát
základními prvky skutečně použitelných kvantových
počítačů.
Velkým problémem je zabránění kvantové dekoherence
qubitů, k čemuž je potřeba dokonale odizolovat
systém od rušivých vlivů okolního prostředí, včetně
tepelných kmitů. Značnou technickou překážkou
praktického použití zatím vyvíjených kvantových
počítačů je proto pracovní teplota. Pro správnou
funkci qubitových obvodů je potřeba je chladit na velmi nízkou
teplotu blízkou absolutní nule (řádově
miliKelviny), což vyžaduje složitou kryogenní
techniku.
Zatím
jsou kvantové počítače ve stádiu experimentálního
ověřování a zdokonalování základních
fyzikálních a technických principů. Manipulace s qubity je
nesrovnatelně obtížnější než s bity v
elektronických počítačích. K vytvoření
skutečně použitelných a výkonných kvantových počítačů
povede ještě dlouhá a obtížná cesta..!..
Po počátečním enthusiasmu je nyní řada
počítačovách odborníků poněkud skeptická ke
kvantovým počítačům. Rozhodně nebudou
"samospasitelné"! Nebudou univerzální, aby mohly
nahradit klasické digitální elektronické počítače (kvantové PC asi nikdy mít doma nebudeme...). Budou vhodné pouze pro některé speciální
oblasti (např. vyhledávání
informací v roszáhlých netříděných datových souborech,
faktorizační rozklad čísel na koeficienty, rychlá Fourierova
transformace, ...), kde mohou podstatně
urychlit klasické algoritmy. Vzhledem ke
kvantově-stochastickému charakteru stavů qubitů používají
kvantové počítače pravděpodobnostní algoritmy (jednotlivé procesy se i milionkrát opakují), se snahou o rychlou opravitelnost a konvergenci. Celé
čistě kvantové (100-%)
počítače nejsou realizovatelné
- a asi by to ani nebylo rozumné. Spíše se bude jednak o kvantové
koprocesory k velkým specializovaným výpočetním
systémům.
Stručná rekapitulace :
Jaké
jsou základní rozdíly mezi klasickou a kvantovou fyzikou
Než se začneme zabývat vlastnostmi mikrostruktury hmoty -
atomy, molekulami, subatomárními částicemi, pro názornost si
zde stručně zrekapitulujeme, jaké jsou nejdůležitější
rozdíly mezi klasickou fyzikou a kvantovou fyzikou a jak tyto
rozdíly ovlivňují naše chápání dějů v přírodě
(pozemské i ve vesmíru) :
-> Měřítka,
velikosti :
Klasická fyzika se zabývá makroskopickými objekty -
předměty kolem nás a jejich systémy, jejich pohybem, silami
působícími mezi nimi, především elektrickými a
gravitačními.
Kvantová fyzika se zaměřuje na chování částic v
mikroskopických měřítcích - molekuly, atomy, subatomární
částice. Jejich pohyby, vzájemnými interakcemi, fyzikálními
poli a jejich kvanty.
-> Dualita
mezi částicemi a vlnami :
Klasická fyzika pracuje s částicemi jako s
odlišnými, lokalizovanými a oddělenými objekty.
V kvantové fyzice mohou částice vykazovat vlastnosti
příslušející zároveň částicím i vlnám. Částice
nejsou lokalizované. Může tak docházet k difrakci a
interferenci.
-> Determinismus
- pravděpodobnost :
Klasická fyzika je deterministická -
předpokládá se, že budoucí chování systému je přesně
určeno počátečními podmínkami v minulosti a lze přesně
předpovědět jaký bude výsledek. Náhodnost se považuje jen
za projev velkého množství interakcí v souborech částic, v
rámci statistické fyziky.
Kvantová fyzika vnáší do popisu pohybu a interakcí
částic stochastickou povahu - kvantobé fluktuace. Můžeme
pouze předpovídat pravděpodobnost určitého výsledku, který
bude v zásadě pokaždé poněkud jiný, i při stejných
výchozích podmínkách. Při mnohonásobném opakování, či
velkém počtu částic, se různé stochastické výsledky
zprůměrují, fluktuace se zahladí a vznikkne naopak velmi
přesný výsledek.
-> Princip
neurčitosti :
V klasické fyzice můžeme všechny
fyzikální veličiny částic, jako je poloha, rychlost,
hybnost, energie, měřit v zásadě s absolutní přesností;
kromě instrumentální přesnosti nám v tom nic nebrání.
V kvantové fyzice se však uplatňuje tzv. princip
neurčitosti (Heisenbergův), podle kterého určité dvojice fyzikálních
veličin, jako je poloha a hybnost částice, není možné
současně změřit s absolutní přesností. Čím přesněji
změříme jednu veličinu, tím neurčitější se stává
druhá veličina. Tato nejistota je zde důsledkem vlnové povahy
částic.
-> Pojetí
fyzikální síly :
V klasické fyzice se každému vzájemnému
působení těles a částic přisuzuje příslušné pole
- prostor, v němž na částice působí určité síly.V
klasické fyzice je to pole elektrické+magnetické a
gravitační. Změny internzity v poli se šíří konečnou
rychlostí (c), což je doprovázeno spojitým přenosem
energie, hybnosti, momentu hybnosti.
V kvantové teorii se pole modeluje jako soubor částic
- kvant pole. A vzájemné silové působení - interakce
částic - je způsobena vzájemnou výměnou těchto kvant - intermediálních
částic. Částice neustále přijímají a vysílají
kvanta intermediálních polí, což vyvolává jejich silová
působení. U elektromagnetických sil jsou intermediálními
kvanty fotony. Ve statickém případě jsou
intermediální fotony virtuální, při dynamickém
působení se virtuální fotony přemění v reálné,
dochází ke skutečnému vyzařování. Fyzikální veličiny se
přenášejí nespojitě po určitých "porcích - kvantech.
V
makroskopickém měřítku jsou kvantové procesy v zásadě
zanedbatelné, klasická fyzika zůstává v naprosté
většině jevů vysoce přesná, fungují podle ní všechny
stroje mechanické a elektrické v průmyslu i domácnosti,
automobily, letadla, kosmické rakety. A přírodní jevy na
pevnině, v moři, jezerech a lesích, v atmosféře, oběhy
planet kolem Slunce atd.
Kvantová
fyzika nám však umožnila chápat skryté atomové a
subatomární jevy, které jsou vnitřní podstatou veškeré
hmoty. Ve vesmíru se podílí na termonukleárních reakcích ve
hvězdách vedoucích k jejich zářivé energii a vzniku prvků ("všichni jsme potomky hvězd"), na vzniku vesmíru a prvotní kosmické
nukleosyntéze. Vedla či napomohla též k vývoji nových
technologií jako jsou tranzistory, integrované obvody, lasery,
pro konstrukci pokročilých elektronických zařízení.
Přispěla též ke konstrukci zařízení pro získávání
energie - fotovoltaika a především jaderná energie.
Kvantová a klasická fyzika se tak čím dál
častěji vzájemně prolínají, pro budoucnost bude zapotřebí
kombinovaný přístup ...
Atomová
struktura hmoty
Otázka stavby a složení
hmoty je jednou z nejzákladnějších a
nejdůležitějších otázek, které lidé kladou přírodě -
spolu s otázkami o původu, velikosti a stavbě vesmíru, či
otázkami vzniku života. V dřívějších dobách, kdy lidé
neměli prostředky k hlubšímu nahlédnutí do mikroskopických
rozměrů nitra hmoty, nebylo nikterak snadné činit jakákoli
věrohodná tvrzení o neviditelné mikrostruktuře hmoty.
Učenci se proto uchylovali k různým domněnkám a hypotézám,
tvořených podle analogií s tím, co pouhým okem vidět bylo.
V tomto kontextu vyvstávala zásadní otázka:
má hmota spojitou či zrnitou
strukturu? Jinými slovy: je hmota neomezeně dělitelná
na stále menší a menší částečky, nebo při tomto dělení
nakonec narazíme na nejmenší, již dále nedělitelné
izolované částečky?
Spletitý
historický vývoj koncepce atomů
Příznivcem této druhé možnosti nejmenších již
nedělitelných částeček byl řecký antický filosof Démokritos
(5.stol.př.n.l., navázal částečně na
názory svého učitele Leukippose Milétského), který argumentoval tím, že kdyby látka byla
neomezeně dělitelná, nezůstalo by nakonec nic, co by neslo
vlastnosti látky. Proto každá látka musí být složena z
nedělitelných částeček, které jsou nositeli vlastností
této látky. Tyto nejmenší nedělitelné částečky nazval
"atomos" - řec. "nedělitelný".
Pozn.: Bylo by
naprostým nedorozuměním považovat Démokrita za objevitele
atomů či za tvůrce atomové teorie! Démokritos o skutečných
atomech nic nevěděl, jeho názor byl jen jednou z mnoha
spekulativních hypotéz, vzájemně rovnocenných na tehdejší
úrovni poznání; jiní učenci tehdy stejným právem
považovali hmotu za neomezeně dělitelnou...
Mimochodem, zmíněná filosofická argumentace o nositelech
vlastností látky, by nyní již neobstála. Víme totiž, že
narůstáním kvantity, či kombinací více kvantit může
vznikat nová kvalita. Vlastnosti systému vznikají až
kombinací vlastností jeho dílčích složek. A stejné je to u
látek. Konkrétní látka nemusí mít žádného
elementárního nositele svých vlastností - tyto vlastnosti
vznikají až specifickým "sestrojením" látky z
částic, které samotné mají úplně jiné vlastnosti...
Představa atomů pak upadla
na dlouhou dobu v zapomění. Teprve od přelomu 17. a 18.stol.,
kdy feudalismus a církev ztráceli svou absolutní moc,
dřívější alchymisty - šarlatánské a často podvodné
"zlatostrůjce" ve službách bohatých a mocných -
postupně nahrazovali seriózní přírodovědci, kteří se již
nepachtili po receptu na výrobu zlata či různých elixírů,
ale snažili se proniknout do skutečné podstaty stavby
hmoty. Tehdy se opět začala objevovat představa o
základních stavebních částicích hmoty (Descartes, Hook) v
souvislosti se zkoumáním chování látek, především plynů
(závislost tlaku na objemu plynu). Od 18.stol., postupným
oprošťováním od dřívějších alchymistických pověr a
předsudků, vznikala chemie jako samostatný
vědní obor. Řadou pokusů dospěli R.Boyl a A.L.Lavoisier k
pojmu chemického prvku jako látky, kterou již
nelze rozložit na dvě či více jiných látek. Při
chemických pokusech byly zjišťovány důležité zákonitosti
chemických dějů :
- Zákon zachování hmotnosti a
energie látek do reakce vstupujících a výsledných
reakčních produktů v uzavřené soustavě (M.V.Lomonosov
r.1748, A.L.Lavoisier r.1774);
- Zákon stálých poměrů
slučovacích (J.L.Proust a J.Dalton r.1799), zákon
násobných poměrů slučovacích (J.Dalton r.1802) a zákon
stálých poměrů objemových (Gay-Lussac r.1805)
pozorovaných při reakcích v plynném skupenství.
Tyto zákony se staly experimentálními podklady
pro vyjasnění otázky vnitřní struktury prvků. Přirozené
vysvětlení všech těchto důležitých zákonitostí podal v
r.1808 J.Dalton ve své atomové hypotéze,
podle níž je každý prvek složen z velkého počtu navzájem
identických atomů, nedělitelných
částic vyznačujících se určitou charakteristickou
hmotností a dalšími vlastnostmi. Atomy téhož prvku jsou
stejné, atomy různých prvků se liší hmotnostmi a dalšími
"chemickými" vlastnostmi. Tyto atomy jsou základní
nedělitelnou stavební jednotku hmoty, která se zúčastňuje chemických
reakcí - slučování prvků spočívá ve spojování
dvou či několika atomů. Zákon zachování hmotnosti při
chemických reakcích je v této koncepci vnějším projevem
nezničitelnosti (a též "nevytvořitelnosti") atomů.
Nový vázaný celek, vzniklý sloučením celistvého počtu
atomů, byl nazván molekula (lat. moles = hmota);
název pochází od A.Avogadra z r.1811, který též zjistil
první vztahy mezi molekulovým, váhovým a objemovým
množstvím látek.
Pozn.: Nyní
víme, že zákon zachování hmotnosti a slučovací poměry se
nepatrně liší od ideálních hodnot. Je to v souvislosti se
vztahem ekvivalence hmotnosti a energie E = m.c2 dáno vazbovou
energií reakce, hmotnostní defektem atomů a jader, rozdílem
hmotnosti protonu a neutronu. Tyto aspekty budou na
příslušných místech rozebírány níže.
Důležitou úlohu pro
poznání složení látek a pro objev řady prvků
sehrála elektrolýza: rozklad látek (většinou jejich vodných roztoků) působením elektrického proudu z Voltových
elektrických článků (baterií). Nejprve to byla elektrolýza
vody na vodík a kyslík, pak elektrolýza různých louhů,
kyselin a solí na vodík, kyslík, sodík, draslík, vápník,
měď, zinek, chrom a další prvky. Vyvstala přitom zajímavá
otázka: "Jestliže elektřina dokáže rozkládat
látky na prvky, mohla by snad i spojovat prvky na složitější
látky?". Anticipovala pozdější poznatek o elektrickém
původu všech chemických reakcí (viz
níže "Interakce atomů").
Periodická tabulka
prvků
V r.1869 se D.I.Mendělejev systematicky zabýval chemickými
vlastnostmi různých prvků. Zjistil, že chemické vlastnosti
prvků periodicky závisejí na jejich
relativní atomové hmotnosti (atomové váze). Navrhl
uspořádat prvky do tabulky, v seřazení podle stoupající
atomové váhy do vodorovných řad (tvořících periody) tak,
aby se prvky podobných vlastností dostaly pod sebe.
Definitivní vysvětlení této Mendělejevovy
periodické tabulky prvků umožnil až rozvoj fyziky
atomů - viz níže "Bohrův kvantový model atomu", pasáž "Obsazování a konfigurace
energetických hladin atomů" a "Interakce
atomů - chemické
slučování atomů - molekuly".
Podobný příběh, vysvětlující podstatu pozorované pravidelnosti
a opakování struktur a vlastností v různých
škálách, se opakoval i v jiných oblastech přírodovědy :
- Ve fyzice částic - §1.5, pasáž
"Unitární
symetrie a multiplety částic"
a část "Standardní model -
jednotné chápání elementárních částic", pasáž "Preonová hypotéza";
- V astrofyzice hvězd - §4.1 "Úloha
gravitace při vzniku a evoluci hvězd" - Hertzprung-Russelův diagram v knize
"Gravitace, černé díry a fyzika prostoročasu".
Na
přelomu 19. a 20.stol., kdy se nashromáždilo dostatečné
množství experimentálních údajů z oblasti chemie a fyziky,
se tedy dospělo k poznání, že čisté prvky jsou složeny z
"nedělitelných" základních částeček - atomů
(ty jsou nositeli jejich vlastností), které se mohou spojovat - slučovat - v molekuly
u sloučenin. Další experimenty na počátku 20.stol. pak
ukázaly, že atom není nedělitelnou
(nestrukturovanou) elementární částečkou, nýbrž má svoji složitou
elektricko-mechanickou strukturu. Z hlediska stavby
hmoty atomy nejsou těmi posledními, nejmenšími a
nejzákladnějšími částicemi látky, ale jen jednou z
důležitých hierarchických jednotek struktury látek.
Struktura atomů
I když tedy fyzika a chemie v průběhu 19.století stále
přesvědčivěji ukazovaly, že látky se skládají z atomů a
molekul, o povaze a stavbě samotných atomů se do konce
19.stol. prakticky nic nevědělo. Že chemické sloučeniny
mají hodně společného s jevy elektrickými
ukázaly již pokusy s elektrolýzou, provedené
M.Faradayem v r.1836. Prvním významným průnikem do struktury
atomu byl objev elektronu, učiněný v r.1895
J.J.Thomsonem při studiu elektrických výbojů v plynech *) a
zjištění, že všechny atomy obsahují elektrony.
*) Elektrické výboje
Elektrické výboje ve vzduchu, známé jako přeskok
jiskry mezi tělesy dostatečně zelektrizovanými statickou
elektřinou, byly známy odedávna (o vývoji
poznatků o elektrických jevech viz též §1.1 "Historický
vývoj poznatků o přírodě, vesmíru, gravitaci", pasáž "Elektřina a magnetismus"
v knize "Gravitace, černé díry a fyzika prostoročasu"). V r.1743 M.Lomonosov vyslovil domněnku,
že blesk a polární záře jsou projevy elektrických výbojů
ve vzduchu (s tím bleskem měl pravdu, u
polární záře se jedná spíše o interakce
vysokoenergetických částic ze Slunce s horními vrstvami
zemské atmosféty). V posledních desítiletích 19.stol.
zkoumala řada badatelů elektrické výboje pod
vysokým napětím ve zředěných plynech (již v
r.1838 M.Faraday pozoroval podivný světélkující oblouk mezi
katodou a anodou, připojenými na elektrické napětí v trubici
se zředěným vzduchem). Používaly se k tomu skleněné
trubice či baňky se zatavenými elektrodami - výbojky,
naplněné vzduchem nebo jinými plyny, zředěnými pomocí
vakuové pumpy na tlak asi 10-3
atmosférického (cca 100 Pa). Nejznámnější byly tzv. Geisslerovy
trubice, používané od r.1850. Tyto různě tvarované
výbojky, krásně svítící v různých barvách (podle druhu
plynové náplně), byly velmi atraktivní; vyvinuly se z nich
"neonové" trubice. Nyní víme, že světelné projevy
elektrického výboje jsou způsobeny ionizací a excitací
atomů plynu, způsobenou nárazy elektronů (urychlených v
elektrickém poli), s následnou deexcitací za vyzáření
fotonů.
 |
|
| Výbojky - plynem plněné trubice s elektrodami, na něž je přiváděno vysoké napětí >100 V | Katodové trubice - velmi zředěným plynem naplněné trubice s elektrodami (výbojky - Crookesovy trubice), na něž je přiváděno velmi vysoké napětí > 1-10 kV |
Později se elektrické výboje zkoumaly v ještě zředěnějších plynech za tlaku kolem 10-6 atm., kdy viditelný výboj již ustává. V letech 1859-76 pozorovali J.Plücker, J.Hittorf a E.Goldstein slabé světélkování baňky naproti katodě: jako kdyby z katody vycházelo nějaké záření, nazvané proto katodové záření. V r.1880 W.Crookes zkonstruoval speciální skleněnou baňku se zatavenými elektrodami, tzv. Crookesovu katodovou trubici, do niž byly mezi katodu a anodu vkládány různé předměty, clony, minerály. Při napětích cca 1000V a vyšších Crookes zjistil, že při dostatečném zředění plynu vycházejí ze směru od záporné elektrody neviditelné tzv. katodové paprsky, způsobující světélkování baňky v místech ležících naproti katodě. Předměty a clony vložené mezi katodu a anodu přitom vrhaly v této luminiscenci ostré stíny, některé minerály vystavené katodovým paprskům světélkovaly. Z Crookesových katodových trubic se vyvinuly vakuové elektronky, obrazovky a rentgenky, přičemž ovšem zředěný plyn byl nahrazen vakuem a studená katoda žhavenou katodou, která termoemisí dodává potřebné elektrony ("katodové paprsky").
 |
| r. 1895: J.J.Thomson - objev elektronů => první model atomu |
J.J.Thomson v r.1895 studoval
vychylování těchto katodových paprsků v elektrickém a
magnetickém poli přičemž zjistil, že katodové paprsky jsou
tvořeny velmi lehkými záporně nabitými částečkami,
jejichž náboj odpovídal elementárnímu elektrickému náboji
(přibližně zjištěnému z Faradayových zákonů elektrolýzy
a později upřesněnému pokusy Millikanovými). Tím objevil
první elementární částice mikrosvěta - elektrony
- a odhalil korpuskulární podstatu katodových paprsků, které
jsou tvořeny proudem rychle letících elektronů. Nyní víme,
že tyto elektrony pocházely z atomů plynu, ionizovaných
nárazy dalších elektronů urychlených v elektrickém poli.
Název elektron (řec. elektron=jantar
; statická elektřina byla v antickém Řecku pozorována na
jantarových předmětech) pochází od
G.J.Stoneye, který se v r.1891 zabýval Faradayovými zákony
elektrolýzy v souvislosti s Daltovou atomovou představou a
přišel k závěru, že elektrické náboje potřebné k
vyloučení jednotlivých druhů atomů jsou celistvými násobky
určitého malého základního, elementárního náboje,
představujícího jakési "atomy" elektřiny
(elektřina byla do té doby považována za nějaké spojité
"fluidum"). Další pokusy s katodovými trubicemi
vedly k objevu X-záření (§3.2 "X-záření - rentgenová diagnostika").
Pozn.:
Elektrickými jevy ve výbojkách a katodových trubicích se v
daném období zabývala řada badatelů, ať již nezávisle
nebo ve vzájemné návaznosti či spolupráci. Je dále
pravděpodobné, že k novým objevným poznatkům přicházeli
ve svých odlehlých laboratořích i badatelé "zapadlí
vlastenci", kteří nepronikli do obecného povědomí.
Přít se proto o partikulární prvenství jednotlivých
konkrétních badatelů může být problematické - a je v
podstatě zbytečné... Důležité je, že společným
bádáním podstatným způsobem přispěli k odhalení
zákonitostí elektřiny a mikrosvěta (srov. též
pasáž "Významné přírodovědecké
objevy - náhoda nebo metoda?"v
§1.0).
Elektrony mají (konvenčně) záporný
elektrický náboj a podle prvních experimentů byly více než
1000-krát lehčí než elektricky neutrální atomy; nyní
víme, že elektrony jsou 1837-krát lehčí než atom vodíku.
Každý atom musí tudíž obsahovat dostatečné množství
kladně nabité hmoty k vyrovnání záporného náboje jeho
elektronů, přičemž tato kladně nabitá složka představuje
téměř veškerou hmotnost atomu. Na základě těchto
zjištění navrhl J.J.Thomson v r.1898 představu, podle níž
jsou atomy miniaturní homogenní koule kladně nabité hmoty, do
níž jsou vnořeny elektrony - obr.1.1.4 vlevo. Tento Thomsonův
model atomu se nazýval též "pudinkový model",
podle své podobnosti s anglickým pudinkem se zapečenými
rozinkami.
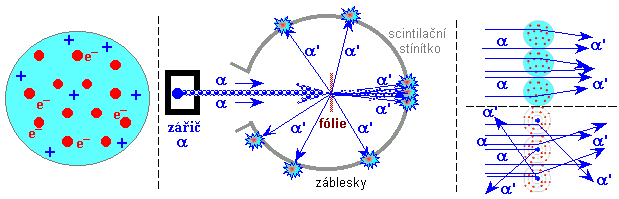
Obr.1.1.4. K vývoji představ o struktuře atomů.
Vlevo: Thomsonův "pudinkový" model
atomu. Uprostřed: Ruthefordovo experimentální
uspořádání rozptylu a-částic kovovou fólií. Vpravo:
Rozdílnost rozptylu a-částic atomy pro případ Thomsonova modelu a modelu
atomu s jádrem.
Detailnějšího experimentálního průzkumu
struktury atomů se ujal E.Rutheford, který se svými
spolupracovníky H.Geigerem a E.Marsdenem prováděli v letch
1909-11 důležité experimenty s rozptylem částic a (o max. energii 7,7MeV, emitovaných přírodním
radionuklidem 226Ra a jeho rozpadovými produkty, především poloniem) při jejich průchodu tenkou zlatou fólií (tloušťky cca 3.10-4mm, což odpovídá kolem 104 atomových vrstev) - obr.1.1.4
uprostřed; částice alfa po průchodu a rozptylu fólií jsou
označeny a'. Tyto částice sledovali Rutheford se
spolupracovníky vizuálně podle záblesků ve scintilační
vrstvě (sirník zinečnatý), kterou byla baňka, obklopující
ozařovanou fólii, zevnitř potažena.
Pozn.: Rozptylové
experimenty (většinou s vysokoenergetickými elektrony
a protony na urychlovačích) jsou obecně nejdůležitější
metodou zkoumání struktury mikrosvěta a vlastností interakcí
částic - viz §1.5 "Elementární
částice".
Podle Thomsonova modelu atomu se očekávalo, že
těžké a rychlé částice alfa snadno "prostřelí"
tenkou zlatou fólii - projdou fólií buď přímo, nebo jen s
malým rozptylem (obr.1.1.4 vpravo nahoře); rovnoměrné
řídké rozložení náboje a hmoty uvnitř
"pudinkového" atomu způsobuje při průchodu
těžkých částic a jen slabé elektrické síly. Prošlé částice alfa
by pak měly zanechat své světelné stopy jen na malé plošce
na zadní straně baňky, v přímém směru od zářiče.
Experiment však ukázal, že řada částic a' se rozptýlila o velký
úhel, některé byly dokonce odraženy do opačného
směru - obr.1.1.4 uprostřed *). Aby se těžké částice alfa
(jsou více než 7000-krát těžší než elektron),
pohybující se vysokou rychlostí (téměř 2.107m/s), takto
rozptýlily, musely na ně uvnitř atomů působit velké
síly, což by nebylo možné u Thomsonova modelu s
poměrně lehkou, řídce rozptýlenou kladnou hmotou v níž
jsou vnořeny lehké elektrony. I když většina částic alfa
snadno pronikla okrajovými částmi atomů, některé z nich se
musely odrazit od "něčeho" malého, těžkého a
kladně nabitého uvnitř atomu.
*) Většina záblesků se sice podle
očekávání objevila na zadní straně baňky v přímém
směru od zářiče, což odpovídalo průletu částic alfa
"mezerami" mezi atomy, daleko od jader. Částice
prolétající vnitřní částí atomů zlata však jevily
značné úhly odklonu.
K objasnění těchto experimentálních
výsledků Rutheford opustil Thomsonův model a navrhl obraz
atomu složeného z velice drobného jádra
(menšího než desetitisícina průměru celého atomu*), v
němž je soustředěn kladný náboj a téměř veškerá
hmotnost atomu, a z elektronů nacházejících se v určité
(relativně poměrně velké) vzdálenosti od jádra. Právě v
okolí tohoto extrémně malého, těžkého a kladně nabitého
jádra, kolem něhož podle Coulombova zákona panují velmi
vysoké intenzity elektrického pole, dochází k účinnému
rozptylu těch a-částic, které prolétají těsně kolem jádra
(obr.1.1.4 vpravo dole). Pokud částice alfa prolétala
poměrně daleko od jádra, nerozptýlila se téměř vůbec.
Čím více se dráha a-částice přibližovala k jádru, tím více se
rozptylovala (vzhledem větším elektrickým odpudivým silám).
*) Pozdější měření ukázaly, že
jádro je dokonce 100 000-krát menší než atom(!) a objasnily
stavbu atomového jádra (je popsáno níže v části "Atomové jádro").
Elektrony v tomto Ruthefordově modelu
atomu však nemohou být v klidu, protože by je elektrostatická
síla přitáhla k jádru a atom by zkolaboval - musejí se
pohybovat, obíhat kolem jádra )* po takových
drahách, kde elektrická přitažlivá síla je vyvážena
odstředivou silou oběhu, analogicky jako je tomu u planet
ve sluneční soustavě - planetární model.
*) V kvantové mechanice se někdy uvádí
i alternativní vysvětlení stavby atomů:
elektrony nemohou spadnout na jádro v důsledku
kvantově-mechanických relací neurčitosti
(diskutovaných výše v části "") a fermionového
charakteru elektronů. Menší vzdálenost, neboli
nižší energetickou hladinu v elektrickém poli jádra než je
ta nejnižší základní, nemohou elektrony nabývat; kdybychom
se je pokusili "natlačit" ještě blíže jádru,
"bránily" by se intenzívní odpudivou silou -
elektrony jako by se svou vlnovou povahou
"nevešly" do tak malého prostoru - jako by trpěly
"klaustrofobním efektem". Vzniká zde tzv. Fermiho
tlak degenerovaných elektronů, který působí proti
elektrickému přitahování jádra. Elektrony se v atomovém
obalu podle Pauliho vylučovacího principu
"párují" do dvojic s opačným spinem v oblastech
prostoru zvaných orbitaly a kvantově-mechanické kmity
plynoucí z korpuskulárně-vlnového dualismu jim zabraňují
zaujímat menší objemy. V našem výkladu se však pro lepší
srozumitelnost a kontinuitu mezi klasickou a kvantovou fyzikou
budeme přidržovat obvyklého "planetárního"
vysvětlení - obíhání elektronů kolem jádra.
Teprve v kvantovém modelu atomu použijeme
korpuskulárně-vlnový dualismus pro vysvětlení kvantování
elektronových orbit (obr.1.1.6) a "klaustrofobní
efekt" kvantových relací neurčitosti použijeme až k
vysvětlení odpudivých sil v jádře v subnukleárních
měřítcích (viz níže část "Silné
jaderné interakce").
Veškerá příroda je
téměř absolutní prázdnota !
Celá naše příroda je pouze prázdnota,
"znečistěná" téměř zanedbatelným množstvím
hmoty. Všechno kolem nás je tvořenou pouze nepatrným
množstvím skutečné - "pevné", koncentrované -
hmoty. Toto poněkud paradoxně znějící tvrzení jednoznačně
vyplývá z poznání struktury atomů. Atom není nějaká
pevná hmotná koule, ale skládá se z velmi hutného jádra o
velikosti jen 10-13cm a téměř prázdného elektronového obalu. Jádro,
nesoucí více než 99,9% hmotnosti atomu, je zhruba 100 000
menší než celý atom. Lze to přirovnat k velkému
sportovnímu stadionu (představujícímu atom), v jehož středu
je položena malá dětská hrací kulička představující
jádro; na zbylé ploše stadionu by kroužilo několik
elektronů a zbytek by byl zcela prázdný. Jak je vidět z
obr.1.1.4 vpravo, energetická částice při střetu s atomem ve
většině případů jím proletí jakoby prázdným prostorem;
pouze pokud náhodou narazí na jádro, dojde k odrazu či
interakci.
Atom je tedy vlastně prázdný prostor,
"znečistěný" několika protony, neutrony a
elektrony. Z asi 99,98% je každý atom tvořen prázdnem,
vakuem. I naše tělo, které je postaveno z těchto atomů, je
převážně tvořeno prázdnotou: celá "skutečná"
hmota našeho těla by se teoreticky dala stlačit do kuličky o
průměru zhruba 1mm, zbytek by tvořila prázdnota. Stejná prázdnota
tvoří i všechny předměty kolem nás...
Hmota je především
pole
Jestliže jsou tedy atomy převážně prázdným
prostorem, při mechanistickém pohledu vzniká paradoxní
otázka: "Jak je možné, že jednotlivé hmotné objekty se
vzájemně neprostupují? Proč pozorujeme
jasné hranice pevných objektů?" - proč neprocházíme
zdí, nebo proč se při sezení "nepropasírujeme" a
nepropadneme skrze židli vlivem gravitační síly? Odpovědí
na tuto paradoxní otázku, proč se hmota za normálních
okolností neprostupuje, je elektromagnetické pole -
síla, vzbuzovaná nabitými protony a elektrony v atomech.
Jestliže se k sobě tělesa těsně přiblíží, jejich atomy
se (vlivem zdeformování elektronové konfigurace) začnou
vzájemně elektricky odpuzovat a za běžných
okolností nemůže dojít k vzájemnému prostupování atomů.
Při sezení na židli se tedy ve skutečnosti vznášíme
("levitujeme") nad horní vrstvou atomů materiálu
židle, na "polštáři" elektrického pole. K
vzájemnému "prostupování" atomů dochází až při
větších silách a energiích, jak je rozebíráno níže v
části "Interakce atomů".
Podobně je tomu s hmotností. Součet klidových
hmotností základních stavebních prvků - kvarků a elektronů
- našeho těla by představoval jen cca 1% hmotnosti našeho
těla (§1.5, pasáž "Kvarková struktura hadronů"). Převážná část
hmotnosti našeho těla (a každého materiálního objektu) je
tvořena kinetickou energií stavebních částic a energií
polí, podle vztahu E = m.c2.
| Gnoseologická poznámka : |
| Trajektorie
a orbity částic <-->
kvantové stavy ? Naše chápání přírody je do značné míry založeno na zkušenosti, vyjádřené v klasické mechanice (a příp. teorii relativity). Proto i při přechodu ke kvantové fyzice pro lepší srozumitelnost používáme představu pohybu částic po určitých trajektoriích a obíhání elektronů po (kvantovaných) orbitách v atomu. Podle názoru současné kvantové fyziky však tyto trajektorie a orbity částic neexistují, částice zaujímají jen určité kvantové stavy..?.. |
| Tento duální gnoseologický pohled budeme reflektovat na řadě míst našeho pojednání o atomech, částicích a fyzice mikrosvěta. |
Planetární
model atomu
E.Rutheford tedy na základě výše zmíněných experimentů s
rozptylem a-částic při jejich průchodu tenkými kovovými
fóliemi sestavil první realistický model atomu - nyní
všeobecně známý planetární model, podle
něhož se atom skládá z kladně nabitého jádra,
kolem něhož obíhají záporně nabité elektrony
(obr.1.1.5 - kde je však planetární
model již ve zdokonalené verzi Bohrova modelu). Přitažlivá elektrická síla, působící
podle Coulombova zákona mezi zápornými elektrony a kladným
jádrem, je vyrovnávána odstředivou silou vznikající při
kruhovém oběhu elektronů.
Pro pohyb elektronu s nábojem -e a
hmotností me v elektrickém Coulombovském poli jádra s nábojem
+Z.e (Z je atomové číslo, nyní nazývané protonové - viz
níže "Atomové
jádro") platí podle
2.Newtonova zákona síly a Coulombova zákona elektrostatiky
pohybová rovnice
me.d2r/dt2 = F
= -(1/4peo).(Ze2/r2).ro,
kde r je polohový vektor od jádra do místa
elektronu, r je okamžitá vzdálenost elektronu od jádra, ro je jednotkový
radius-vektor směřující od jádra k elektronu. Jádro se
přitom považuje za nehybné a nekonečně těžké ve
srovnání s hmotností elektronu me. Tato pohybová rovnice vyjadřuje pohyb elektronu v
centrálním poli jádra po Kepplerových dráhách (obecně
elipsa, hyperbola, parabola), podobně jako je tomu u pohybu
planet v centrálním gravitačním poli (podrobný matematický
rozbor je v §1.2 "Newtonův gravitační zákon" monografie "Gravitace, černé díry a
fyzika prostoročasu"). V nejjednodušším případě
kruhové dráhy poloměru r dostáváme jednoduchou
pohybovou rovnici
me.v2/r = (1/4peo).Ze2/r2,
udávající oběhovou rychlost v elektronu v závislosti
na poloměru oběhu r. Tuto základní rovnici
planetárního modelu atomu můžeme též jednoduše získat
jako podmínku rovnováhy odstředivé síly me.v2/r, působící na
elektron při kruhovém pohybu, a přitažlivé elektrické síly
(1/4peo).Ze2/r2 jádra podle Coulombova zákona.
Původní planetární model
však měl nedostatek v tom, že byl v rozporu s klasickou
elektrodynamikou: Podle Maxwellových rovnic elektrodynamiky
každý elektrický náboj, pohybující se se zrychlením,
vyzařuje elektromagnetické vlny. Takže každý elektron
obíhající kolem jádra (kruhový pohyb
je nerovnoměrný - mění se směr vektoru rychlosti -
dostředivé zrychlení) by měl vytvářet
periodicky proměnné elektromagnetické pole, které by se
projevovalo vyzařováním elektromagnetických vln,
odnášejících kinetickou energii obíhajícího elektronu - viz §1.5 "Elektromagnetické pole.
Maxwellovy rovnice.",
Larmorův vzorec (1.61'), monografie "Gravitace,
černé díry a fyzika prostoročasu". Takto brzděný elektron by ve spirále obíhal a
klesal stále blíže a blíže k jádru, intenzita a frekvence (rovná frekvenci kruhového pohybu elektronu) vyzařování by se zvyšovala, až by elektron nakonec
dopadl na jádro *). Takový "elektrický kolaps"
planetárního atomu by přitom proběhl velmi rychle, asi za 10-10 sekundy pro atom
vodíku.
*) Dosazením do zmíněného Larmorova
vyzařovacího vzorce -(dE/dt) = (2/3).(1/4peo).q2a2/c3 náboje elektronu q=e
a zrychlení jeho kruhového pohybu a = v2/r = (1/4peo)Ze2/mer2 dostaneme pro
časovou změnu poloměru oběhu r (zmenšování r,
klesání po spirále) diferenciální vztah dr/dt = -(4/3).(1/4peo).(Ze4/me2c3r2). Integrací jeho
inverzního tvaru od r(t=0) = rat - původní poloměr atomu rat » 10-10m ve výchozím čase t=0, do r(t=tcol) = rnuc - dopad na jádro poloměru rnuc » 10-14m, dostaneme pro čas kolapsu tcol hodnotu tcol = (4p2eo2me2c3/Ze4).(rat3 - rnuc3) » 10-10/Z [sec].
Nic takového ovšem naštěstí nepozorujeme -
atomy zde existují a jsou stabilní! Kromě toho by atomy s
elektrony na nejrůznějších oběžných drahách vysílaly spojitě
různé frekvence elektromagnetického záření, což je v
rozporu s experimentálně pozorovanými diskrétními spektry
záření atomů, složenými z jednotlivých spektrálních
čar o přesně daných vlnových délkách (frekvencích a energiích),
charakteristických pro různé atomy (viz
níže "Záření
atomů").
 |
Obr.1.1.5. Schématické
znázornění planetární stavby atomu, v němž
záporné elektrony obíhají kolem kladně nabitého
jádra.. Podle Bohrova modelu obíhají elektrony kolem jádra pouze po kvantovaných diskrétních dráhách, na nichž nevyzařují. Při přeskoku elektronu z vyšší na nižší dráhu se příslušný rozdíl energií vyzáří jako kvantum (foton) elektromagnetického záření. |
| Je to
atom ? Při pohledu na tento obrázek téměř každý vzdělaný člověk řekne, že "je to atom". Tato odpověď je správná jen částečně, protože ve skutečnosti se jedná jen o model atomu. Kdybychom se ve sci-fi představě dokázali zmenšit na pidimužíky velikosti jednoho pikometru a vnikli do atomu, žádné "kuličky" - elektrony, obíhající kolem jiné "kuličky" - jádra, bychom neviděli. Mohli bychom vidět nanejvýš jen fluktuující a vlnící se pole, s různou hustotou rozložené kolem orbitalů. Tento nákres je však docela výstižný (srov. s pasáží "Kuličkový model" v §1.5 "Elementární částice"), dovede názorně zobrazit a pochopit většinu důležitých procesů v atomech - excitace a deexcitace, emise fotonů charakteristického záření, chemické slučování atomů, procesy interakce atomů s ionizujícím zářením, vnitřní konverzi záření gama a X s emisí konverzních a Augerových elektronů, další doprovodné jevy při radioaktivitě.... Proto jej budeme často používat. |
|
Bohrův kvantový model
atomu
Zmíněný vážný nedostatek planetárního modelu atomu
napravil r.1913 dánský fyzik Niels Bohr, který na základě
experimentálních poznatků a v duchu idejí tehdy vznikající kvantové
mechaniky doplnil původní planetární model atomu o
tři důležité postuláty :
Planetární model, doplněný těmito třemi postuláty, představuje proslulý Bohrův model atomu (obr.1.1.5), který úspěšně vysvětluje nejdůležitější kvantové vlastnosti stavby atomu, m.j. diskrétní (nespojitá) čárová spektra záření vysílaného atomy (viz níže). Bohrův model si svou platnost zachoval dodnes (s příslušnými zobecněními zmíněnými níže).
Atom a
planetární soustava: podobnosti a rozdíly
Po zjištění skutečnosti, že atom je systémem kladně
nabitého jádra a záporně nabitých elektronů vázaných
elektrickou silou, se inspirací pro vyjasnění struktury tohoto
systému stala již dobře prozkoumaná Sluneční soustava,
vázaná gravitační silou. Je zde zjevná analogie
ve třech bodech :
Na základě těchto analogií vznikl Ruthefordův planetární model atomu. Mezi planetární soustavou a atomem jsou však i zásadní rozdíly :
Tyto rozdílnosti si vynutily výše
uvedenou Bohrovu modifikaci planetárního modelu atomu. Přesto
se ale při některých názorných kvalitativních úvahách
planetární představa atomu dosud užívá.
Jedním z hlavních rozdílů mezi klasickým
elektro-mechanickým a kvantovým chápáním atomů je mechanismus
záření atomů. Záření z atomů není vyzařováno
plynule, ale po kvantech a frekvence záření f není
dána frekvencí periodického oběhu elektronů, ale
energetickým rozdílem E stacionárních orbit
elektromů, v kombinaci se vztahem E = h.f mezi energií
elektromagnetického kvanta (fotonu) a frekvencí f
příslušné elektromagnetické vlny (srov. výše uvedený
"Korpuskulárně-vlnový
dualismus").
Atomy jsou nesmírně
prázdné !
Srovnáme-li typickou velikost atomu 10-8cm, dráhy oběžných drah elektronů a rozměr
hutného jádra 10-13cm, vidíme jak nesmírně prázdný je atom:
celých 99,9999999999999 % objemu atomu tvoří prázdný
prostor (vakuum). Tento zdánlivě prázdný prostor je
však vyplněn intenzívním elektrickým
(elektromagnetickým) polem, které dává atomu
charakter pevného objektu.
Proč
atomy v klidu nezáří? - vlnový mechanismus
kvantování
Mechanismus kvantování v Bohrově modelu atomu lze
nejnázorněji pochopit pomocí představy o
korpuskulárně-vlnovém chování elektronu při jeho pohybu na
oběžné dráze kolem atomového jádra. Budeme nejdříve
uvažovat nejjednodušší případ - atom vodíku.
Z korpuskulárního hlediska na elektron o hmotnosti me a náboji -e,
obíhající kolem protonu o náboji +e po kruhové dráze
poloměru r rychlostí v, působí odstředivá
síla FC=
mev2/r a Coulombovská
přitažlivá elektrostatická síla FE= (1/4peo).e2/r2. Podmínka rovnováhy
(stability) dráhy pak je FC=FE, tj. mev2/r
= (1/4peo).e2/r2, z čehož pro poloměr dráhy a oběžnou rychlost
elektronu plynou vztahy
| e2
e r = ---------------- , v = ----------------- . 4peomev2 Ö(4peomer) |
Při splnění těchto vztahů by však
elektron podle klasických představ mohl obíhat v libovolné
vzdálenosti r od středu atomu.
Z vlnového hlediska je možno obíhající elektron
považovat za vlnu, jejíž Broglieho vlnová délka je l = h/mev. Aby takováto
"elektronová vlna" mohla trvale a plynule obíhat po
dráze poloměru r, musí se na tuto dráhu
"uložit" celistvý počet vlnových délek
l
elektronu, tj. buď jedna úplná Broglieova elektronová vlna l, nebo 2 vlnové
délky na obvod 2pr, 3l/obvod, 4l/obvod atd. - obr.1.1.6 nahoře. Jen tehdy všechny
elektronové vlny na sebe hladce navazují
podél celého obvodu dráhy. Pokud by podél dráhy vznikl
necelý počet vlnových délek (obr.1.1.6 dole), vlnová
návaznost se poruší a dráha nebude stabilní, dojde k
diskontinuitě a rušivé interferenci, která se zformuje do
kvanta elektromagnetického záření - vyzáří se foton,
který odnese příslušné množství energie a elektron přejde
na nejbližší stabilní dráhu s celočíselným počtem
Broglieho vlnových délek.
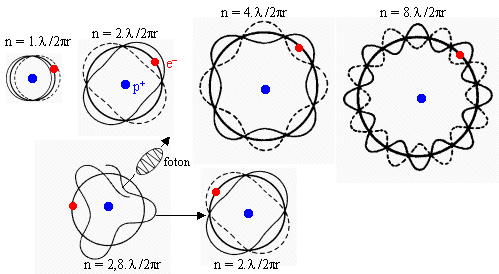
Obr.1.1.6. Nahoře: Elektron obíhá kolem
jádra po stabilní dráze neomezeně dlouho a bez vyzařování,
pokud jeho dráha obsahuje celočíselný počet n
Broglieho vlnových délek elektronu. Dole: Při
necelistvém počtu vlnových délek je porušena "vlnová
návaznost" a dráha je nestabilní - dochází k
vyzáření fotonu a elektron přejde na stabilní dráhu s
celočíselným počtem vlnových délek.
Kruhová dráha poloměru r má obvod 2pr, takže podmínka
pro stabilitu dráhy zní
2p rn = n . l , n = 1,2,3,4, .....,
kde rn
označuje poloměr dráhy jež obsahuje n vlnových délek
l = h/mev. Dosazením za
oběžnou rychlost z planetárního modelu v = e/Ö(4peomer)
dostáváme, že stabilní jsou jen ty elektronové dráhy,
jejichž poloměr je dán vztahem
| h2 eo rn = n2 ------------ , n = 1,2,3, ..... . p me e2 |
Pro n=1 dostáváme nejnižší
(základní, neexcitovanou) orbitu elektronu v atomu vodíku o
poloměru r1 = 0,529.10-8cm. Tato hodnota se nazývá Bohrův poloměr
a považuje se též za jednu z modelových hodnot poloměru
elektronu re (viz diskusi v §1.5, pasáž
"Velikost elementárních
částic...").
Celé číslo n se
nazývá hlavní kvantové číslo a určuje
nejen pořadí "dovolené" kvantové dráhy, ale také
energii elektronu na dané kvantové dráze:
Celková energie E elektronu na oběžné dráze je dána
součtem jeho kinetické energie Ek= (1/2)mev2 a potenciální energie Ep = -e2/(4peor) v Coulombově
elektrickém poli jádra (bod nulového
potenciálu volíme v nekonečnu; znaménko "-"
značí, že síla působící na elektron je přitažlivá). Tedy E = Ek + Ep = mev2/2
- e2/(4peor), což po dosazení v = e/Ö(4peomer)
dává E = e2/(8peor). Pro dovolené
dráhy orbitálního poloměru rn pak vycházejí diskrétní hodnoty energie
En :
| me e4 1 En = - ---------- . ---- , n = 1,2,3, ..... , 8eo h2 n2 |
které se označují jako energetické
hladiny či slupky. Tyto hladiny jsou
všechny záporné (souvisí to s tím, že
jsme potenciál elektrostatického pole zvolili nulový v
nekonečnu), což značí, že kinetická
energie elektronu na kvantové dráze nestačí k tomu, aby se
elektron vyprostil z přitažlivé síly jádra a unikl z atomu.
Absolutní hodnota energie elektronu |En| udává práci
(energii), kterou bychom museli elektronu dodat, abychom jej
přenesli z dané kvantové dráhy n do nekonečna, tj.
vyprostili z přitažlivosti jádra, čili uvolnili jej z atomu.
Obíhá-li elektron na nejnižší kvantové
dráze n=1, říkáme že je v základním
(nevzbuzeném) stavu. Přechod na vyšší kvantovou dráhu je
možný jen dodáním energie - vzbuzením
neboli excitací atomu, k němuž může dojít
buď absorbcí fotonu, nebo působením Coulombových
elektrických sil při průletu nabité částice či nárazu
dalšího atomu (při vyšší teplotě). Při přechodu z této
vyšší energetické hladiny n na nižší energetickou
hladinu n-1, tj. při deexcitaci, se
energetický rozdíl vyzáří ve formě kvanta
(fotonu) elektromagnetického vlnění o energii E = En-1-En a vlnové délce
.....
Je-li elektronu dodána energie vyšší než vazbová |En|, uvolní se elektron z pole jádra a vyletí ven -
dojde k ionizaci atomu.
Zdokonalený
Bohrův model; kvantová čísla
Původní Bohrův model se vztahoval na atom vodíku a uvažoval
jen kruhové orbity elektronů. Se zdokonalováním
experimentálních spektrometrických metod se ukázalo, že
spektrální čáry atomů nejsou jednoduché, ale dvojité i
vícenásobné - spektra vykazují jemnou strukturu.
Pro vysvětlení této jemné struktury Bohrovi následovníci,
zvláště A.Somerfeld, doplnili a zdokonalili původní Bohrův
model atomu.
Vedle kruhových drah byly navrženy i eliptické
dráhy elektronů s delší (hlavní) poloosou danou hlavním
kvantovým číslem n, přičemž vedlejší (kratší)
poloosa je charakterizována druhým kvantovým číslem l,
které může nabývat diskrétních hodnot z rozmezí 0 Ł l Ł n-1. Toto
kvantové číslo l, dříve označované jako vedlejší
kvantové číslo, se nyní nazývá orbitální
kvantové číslo a určuje velikost momentu
hybnosti Ml elektronu na dané dráze (orbitu). Kvantově
mechanický rozbor dává pro moment hybnosti kvantové hodnoty :
Ml = (h/2p) . Ö[l(l-1)] , l = 0, 1 ,2, ......, n-1.
Duplicita a jemná struktura spektrálních čar se pak dá
vysvětlit přechody mezi energetickými hladinami s různým
kvantovým číslem n na různé podhladiny
lišící se hodnotou l, na níž celková energie E
závisí jen málo.
Elektron obíhající rychlostí v po
kruhové dráze poloměru r představuje z elektrického
hlediska miniaturní proudovou smyčku protékanou elektrickým
proudem I = e.v/2pr (v/2pr udává, kolikrát prošel elektron s nábojem e
daným bodem dráhy za jednotku času). Tato proudová smyčka
vzbuzuje magnetické pole a její magnetický
moment je me = pr2.I = r.e.v/2 = (e/2me).me.r.v = (e/2me).M, kde M je
oběžný moment hybnosti elektronu. Jelikož moment hybnosti M
je kvantován (Ml = l.h/2p, l = 0,1,2, ......, n-1), orbitální magnetický
moment elektronu me na dané kvantové
dráze je
me = ml . e h / 2me = ml . mB , ml = 0, ±1, ±2, ....., ±l ,
kde ml je magnetické
kvantové číslo a konstanta mB se nazývá Bohrův magneton
(představuje nejmenší, elementární kvantum magnetického
momentu).
Vedle orbitálního magnetického momentu,
vyvolaného pohybem elektronu po oběžné dráze, má elektron
ještě svůj vlastní tzv. spinový magnetický moment
a svůj vlastní "rotační" moment hybnosti - spin.
Tyto vlastnosti se často zjednodušeně
vysvětlují rotací elektronu kolem vlastní osy - rotující
elektron by měl svůj rotační moment hybnosti a
odpovídající magnetický moment. Toto vysvětlení však není
konzistentní, neboť "obvodová rychlost" elektronu by
musela značně převyšovat rychlost světla (v rozporu se
speciální teorií relativity) a nebylo by možné vysvětlit,
jaká síla kompenzuje obrovskou odstředivou sílu a udržuje
elektron pohromadě. Spin je nutno považovat za čistě
kvantovou vlastnost částice, pro kterou nemáme přesný
klasický model.
Pro vlastní moment hybnosti, tj. spin elektronu, pak
platí, že jeho průmět do osy rotace může nabývat jen dvou
hodnot: buď - 1/2h, nebo + 1/2h; spinový magnetický
moment elektronu je pak dán Bohrovým magnetonem: ±mB. Pro vlastní moment hybnosti elektronu Ms a spinový
magnetický moment elektronu ms platí: Ms = s . h , ms = -(e/me).Ms = ±mB, kde s=1/2 nebo -1/2.
Číslo s se nazývá spinové číslo a
u elektronu může nabývat hodnot ±1/2 (v §1.5 "Elementární
částice" se setkáme s částicemi, např. mezony p, u nichž jsou
možné tři hodnoty spinového čísla: -1, 0, +1).
Interakce mezi magnetickými poli buzenými
spinovým a orbitálním momentem hybnosti elektronů, tzv. spin-orbitální
interakce, vede k rozštěpení energetických hladin
elektronů v atomech na blízko sebe ležící
"podhladiny", což se ve spektrech záření z atomů
projevuje příslušným rozštěpením spektrálních čar na jemnou
strukturu.
Např. u vodíku je nejnižší
energetická hladina elektronu n=1 rozštěpena na dvě
podhladiny se souhlasným a nesouhlasným spinem elektronu a
protonu. Přechod mezi těmito dvěma stavy odpovídá pohlcení
nebo vyzáření elektromagnetického záření o vlnové délce
21cm. Emise a absorbce tohoto záření atomárního vodíku je
velmi důležitá při radioastronomickém pozorování
vzdáleného vesmíru.
a - konstanta jemné
struktury
Pro stavbu atomů (a též i atomových jader) má obzvláštní
důležitost, s jakou silou interagují částice s
elektromagnetickými poli. Obecně je tato síla vyjádřena
Coulombovým zákonem elektrostatiky a Lorentzovou silou
působící na náboj pohybující se v magnetickém poli. V
kvantové fyzice, kde je elektrický náboj kvantován v
násobcích elementárního náboje elektronu e, vystupuje
zajímavý poměr, který vyjadřuje elektrické, kvantové a
relativistické vlastnosti elektromagnetických interakcí
nabitých částic ve vakuu: je to tzv. konstanta jemné
struktury *)
a = e2/2eohc =
0,0072973525376 = 1/137,03599968 ,
kde e je elementární náboj elektronu, h Planckova
konstanta (redukovaná), c rychlost světla, eo elektrická permitivita vakua. Konstanta jemné
struktury je bezrozměrná veličina, její
číselná hodnota nezávisí na volbě jednotek.
*) Název pochází z toho, že tato
konstanta vystupuje ve vztazích pro rozštěpení spektrálních
čar záření atomů do jemné struktury vlivem tzv. spin-orbitální
interakce mezi spinovým a orbitálním momentem hybnosti
elektronů, resp. mezi jimi buzenými magnetickými poli. Tuto
konstantu již v r.1916 poprve použil jeden z průkopníků
atomistiky A.Sommerfeld při studiu jemné struktury
elektronových hladin v atomu. Vyextrahoval tuto bezrozměrnou
hodnotu s dřívější Rydbergovy konstanty vyjadřující
vlnové délky spektrálních čar při přeskocích elektronů
mezi jednotlivými hladinami v atomu a interpretoval ji jako
míru relativistické odchylky spektrálních čar o Bohrova
modelu (poměr rychlosti v1 elektronu na první orbitě Bohrova modelu atomu
vodíku k rychlosi světla ve vakuu a = v1/c).
Tato důležitá fyzikální konstanta charakterizuje sílu
elektromagnetické interakce, vystupuje jako vazbová
konstanta v kvantové elektrodynamice. Spoluurčuje
vlastnosti atomů, molekul a z nich složených látek, jakož i
vlastnosti atomových jader včetně jaderných reakcí. Občas
se diskutuje o možné proměnnosti základních
přírodních konstant v průběhu evoluce vesmíru,
přičemž konstanta jemné struktury by mohla být vhodným
nástrojem k citlivým spektrometrickým analýzám záření ze
vzdáleného vesmíru (viz též pasáž "Původ
přírodních konstant" v
§5.5 "Mikrofyzika a kosmologie" monografie
"Gravitace, černé díry a fyzika prostoročasu").
| Gnoseologická poznámka : |
| Trajektorie
a orbity částic <-->
kvantové stavy ? Naše chápání přírody je do značné míry založeno na zkušenosti, vyjádřené v klasické mechanice (a příp. teorii relativity). Proto i při přechodu ke kvantové fyzice pro lepší srozumitelnost používáme představu pohybu částic po určitých trajektoriích a obíhání elektronů po (kvantovaných) orbitách v atomu. Podle názoru současné kvantové fyziky však tyto trajektorie a orbity částic neexistují, částice zaujímají jen určité kvantové stavy..?.. |
| Tento duální gnoseologický pohled budeme reflektovat na řadě míst našeho pojednání o atomech, částicích a fyzice mikrosvěta. |
Obsazování a
konfigurace elektronových hladin atomů
Přejděme nyní od atomu vodíku ke složitějším atomům s
více elektrony. Představme si, že jsme vytvořili jádro se Z
protony a umístíme jej do prostoru obsahujícího volné
elektrony. Elektrickými silami bude toto jádro přitahovat
elektrony, které budou postupně obsazovat jednotlivé
"dovolené" kvantové orbity kolem jádra tak dlouho,
až se vytvoří elektronový obal tvořený Z elektrony a
atom se stane elektricky neutrální.
Elektronové
orbity, slupky, hladiny, orbitaly
Elektronové orbity jsou kvantovány, takže z energetického
hlediska by bylo nejvýhodnější, kdyby všechny elektrony
obsadily nejnižší energetickou hladinu s hlavním kvantovým
čístem n=1. Takové "natěsnání" elektronů na
jednu hladinu se však neuskutečňuje. Naopak, podle tzv. Pauliho
vylučovacího principu *) ve stejném kvantovém stavu
může být pouze jeden elektron, takže pokud jsou nejnižší
energetické hladiny obsazeny, musejí další elektrony
obsazovat stále vyšší a vyšší hladiny.
*) Tento vylučovací princip odvodil
švýcarský fyzik W.Pauli v r.1925 na základě řady
experimentálních zkoumání rozložení elektronů v atomech.
Později byl tento vylučovací princip teoreticky zdůvodněn
jako důsledek kvantově-statistického chování částic s
antisymetrickými vlnovými funkcemi (vůči transpozici
částic) - tzv. fermionů, mezi něž elektrony
patří (viz §1.5 "Elementární částice").
S použitím Pauliho vylučovacího principu
můžeme stanovit, kolik elektronů může současně obíhat v
drahách (podslupkách) příslušných k hlavnímu kvantovému
číslu n: je zde možných n-1 hodnot orbitálního
kvantového čísla l, přičemž pro každé l
existuje 2.l +1
různých hodnot magnetického kvantového čísla ml a dále dvě možné
hodnoty spinového magnetického čísla ms (+1/2,-1/2). Každá podslupka tedy může obsahovat
maximálně 2.(2.1+1) elektronů a každá slupka s hlavním
kvantovým číslem n maximálně n-1 těchto podslupek,
tj. maximálně celkem
l=0Sn-12.(2.l - 1) = l=0Sn-14.l + 2.n = 4.(n-1).n/2 + 2n = 2 n2
elektronů. Uvedený soubor elektronů tvoří n-tou
slupku (sféru, hladinu) atomu. Tyto energetické
hladiny, odpovídající diskrétním hodnotám hlavního
kvantového čísla n, se označují písmeny (ve směru
zevnitř od jádra): K, L, M, N, O, P. Počet elektronů, které
mohou obíhat na dané hladině, není tedy libovolný, ale je omezený
maximálním číslem 2n2 :
K(n=1) : max. 2 elektrony , L(n=2)
: max. 8 elektronů, M(n=3): max. 18 elektronů,
N(n=4): max. 32 elektronů, O(n=5):
max. 50 elektronů, P(n=6): max. 72 elektronů.
Elektrony obsazují dráhy postupně,
počínajíc slupkou K.
Tento systém obsazování elektronových slupek
a podslupek v atomech, spolu s analýzou vazbové elektrické
síly elektronů, umožňuje pochopit nejdůležitější
zákonitosti chemického chování prvků.
Seřadíme-li chemické prvky v pořadí podle atomového
čísla, opakují se prvky s podobnými chemickými a
fyzikálními vlastnostmi v pravidelných intervalech. Tento
empiricky zjištěný periodický zákon zformuloval
D.I.Mendělejev v r.1869 ve své periodické tabulce
prvků, která byla jeho následovníky doplněna a
zpřesněna do nynější podoby (viz
níže část "Interakce atomů", pasáž "Periodické chemické
vlastnosti atomů").
Z rozboru elektronových konfigurací
především plyne, že elektrony v plně obsazené slupce,
označované jako uzavřená slupka, jsou silně
vázané, neboť kladný náboj jádra značně převyšuje
záporný náboj vnitřních elektronů způsobujících
elektrické "stínění". Rozdělení efektivního
náboje v atomu obsahujícím pouze uzavřené slupky je dokonale
symetrické, atom nemá žádný dipólový moment, nepřitahuje
jiné elektrony a jeho vlastní elektrony jsou silně vázané.
Takové atomy nevstupují do chemických vazeb, jsou chemicky inertní
- to se projevuje u hélia 2He, neonu 10Ne, argonu 18Ar, kryptonu 36Kr, xenonu 54Xe, radonu 86Rn *).
*) Plně obsazená sféra K je u
hélia a plně obsazené sféry K a L u neonu. U
těžších inertních plynů Ar, Kr, Xe, Rn však k inertnímu
chování stačí zaplnění vnější slupky jen 8 elektrony,
což souvisí se závislostí vazbové energie na orbitálním
kvantovém čísle, v důsledku čehož se zaplnění některých
podslupek může stát energeticky nevýhodným.
Naproti tomu
atomy s jedním elektronem ve vnější slupce tento elektron
snadno ztrácejí, neboť je slabě vázán: je poměrně daleko
od jádra, jehož náboj vnitřní elektrony odstiňují na
efektivní hodnotu pouze +e - tím se vysvětluje vysoká
chemická reaktivnost alkalických kovů (a též vodíku) s
valencí +1. Naopak atomy, jimž ve vnější slupce chybí k
uzavřenosti jeden elektron, se snaží tento elektron získat
přitažlivou silou neúplně odstíněného jaderného náboje,
což vysvětluje např. zvýšenou reaktivitu halogenů. O
chemických reakcích viz níže část "Interakce
atomů", pasáž "Chemické
slučování atomů - molekuly".
Orbitaly
V důsledku vlnových-stochastických zákonitostí kvantové
fyziky elektrony v atomovém obalu neobíhají po přeně
stanovené dráze (orbitě), je možné určit pouze
oblast ve které se elektron nachází s určitou pravděpodobností.
Oblast, ve které je nejvyšší pravděpodobnost
výskytu elektronu (>95%) se nazývá orbital.
Elektrony ve slupce jsou seskupeny do jemnějších prostorových
konfigurací, orbitalů, v závislosti na vedlejším
(orbitálním) kvantovém čísle l,
které určuje typ orbitalu a hodnotu magnetického momentu
elektronu (bylo rezebíráno výše). V dané slupce se podle
rostoucího vedlejšího kvantového čísla orbitaly označují
postupně písmeny s,p,d,f. Na základní slupce
n=1 je pouze jeden orbital 1s, na slupce n=2 jsou
orbitaly 2s a 2p, ..., na slupce n=4 mohou být
postupně orbitaly 4s, 4p, 4d, 4f.
V důsledku kvantového vylučovacího principu elektrony
obsazují postupně s-orbital slupky K, následují s-
a p-orbitaly slupky L, s-, p- a d-orbitaly
M slupky atd... Každý orbital se zaplňuje jedním a pak i
druhým elektronem s opačnými spiny. Způsob obsazování
orbitalů se někdy nazývá Hundovo pravidlo. Orbitaly
mohou být různě orientovány v prostoru, podle magnetických
kvantových čísel m (nabývá hodnot
-l,...,0,...+l). Tyto orbitaly stejného typu, které se liší
jen prostorovou orientací, mají stejnou energii - jsou energeticky
degenerované.
Je-li atom
vložen do vnějšího magnetického pole, původně jednotná
energie elektronů v rámci orbitalu se rozestoupí do několika
různých (i když blízkých) energetických hladin, podle
příslušnosti k odlišným orientacím orbitalů. Pohyb
každého elektronu uvnitř slupky totiž vytváří magnetický
moment (jehož vektor závisí na
prostorovém uspořádání orbitalů), na
který ve vnějším magnetickém poli působí síla. Tato
interakce vede k jemnému rozštěpení energetických hladin
elektronů. K velmi jemnému rozestoupení energetických hladin
uvnitř orbitalů dochází i vlivem opačných spinů
(+1/2, -1/2) elektronů (Stern-Gerlachův
pokus).
Označení atomů
prvků
V souvislosti se stavbou atomových jader (viz
níže část "Atomová jádra") jsou atomy charakterizovány dvěma základními
parametry:
- Protonové číslo Z (dříve
nazývané atomové číslo A), udávající
počet protonů v jádře - a u neutrálního (neionizovaného)
atomu i počet elektronů v obalu. Je tím dána i pozice prvku v
Mendělejevově periodické tabulce prvků.
- Nukleonové číslo N (dříve
nazývané hmotové číslo) udává celkový počet
nukleonů v jádře atomu - součet protonů a neutronů.
Charakterizuje hmotnost atomu (neboť nukleony v jádře
představují více než 99,99% hmotnosti atomu).
Běžně používaný způsob zápisu těchto čísel u
určitého prvku X je pomocí dolního a horního indexu: NXZ. Např. vodík 1H1,
dusík 14N7, sodík 23Na11. Podrobněji bude
rozebíráno níže v části "Atomová jádra".
Excitace
a spektra záření atomů
Podle Bohrova modelu vzniká elektromagnetické záření v
elektronových obalech atomů tehdy, když elektrony
přecházejí z vyšších hladin na nižší. Jelikož
energetické hladiny atomů jsou kvantovány, jsou z obalu atomu
vyzařovány fotony záření o zcela určitých energiích -
spektrální rozložení energií a vlnových délek není
spojité, ale diskrétní.
Excitace, deexcitace a ionizace atomů
Excitace
atomů
K tomu, aby mohlo dojít k přechodu elektronu z vyšší
na nižší hladinu, musí být atomu předtím dodána
energie vedoucí k jeho excitaci *) - k
přechodu elektronu na vyšší energetickou hladinu. Tato
energie může být dodána buď Coulombickou elektromagnetickou
interakcí přilétající nabité částice (elektronu, protonu,
srážky s jiným atomem), nebo fotonovým zářením.
*) Uvažujeme zde "již hotové"
atomy, nikoli situaci, kdy atomy teprve vznikají - vznik atomů
je samozřejmě rovněž doprovázen kvantovými excitacemi a
vyzařováním.
Za běžných okolností dochází k excitaci
elektronových hladin v atomech s hlavním kvantovým číslem n
většinou na hodnoty n+1, n+2 či (n+několik málo hodnot)
hlavního kvantového čísla n. Pomocí silných impulsů
elektrického pole se však elektrony mohou dostat i do vysoce
excitovaných stavů s hodnotami n~100 i více. Takové atomy s
vysoce excitovanými elektrony se někdy nazývají Rydbergovy
atomy (podle J.R.Rydberga,
který měřil spektra excitovaných atomů, především
vodíku, počátkem 20.stol.). Průměr
takových atomů již dosahuje makroskopických rozměrů
řádově mikrometry. Sofistikovanými metodami s kombinací
laserového a mikrovlnného záření se podařilo připravit
excitované atomy s rozměry téměř jeden milimetr!
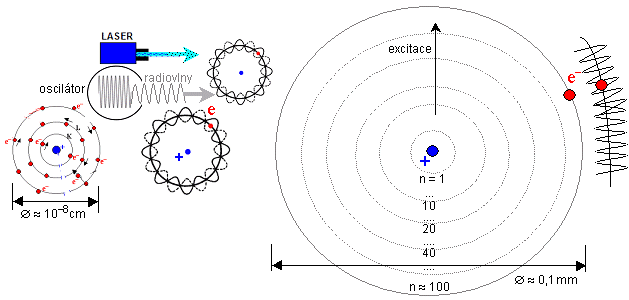
Silnými elektrickými impulsy nebo
zářením se elektrony v atomech mohou dostat i do vysoce
excitovaných stavů - vznikají Rydbergovy atomy.
Důležitou vlastností
Rydbergovských atomů je jejich vyšší citlivost na gradient
elektrického pole. To umožňuje "operativně"
manipulovat s atomy v náročných atomových a částicových
experimentech - viz např. §1.5, pasáž
"Umělá výroba antihmoty".
Excitované atomy jsou samy o sobě zpravidla
velmi nestabilní. Deexcitují buď jednorázově na
základní stav s emisí viditelného nebo UV světla, nebo i
přeskoky mezi vyššími hladinami s emisí mikrovlnného
záření. Rydbergovské
valenční elektrony jsou excitovány do vysokých orbitalů
značně vzdálených od jádra. Poněkud neočekávaným
důsledkem vysoké excitace elektronů do velkých hodnot
hlavního kvantového čísla je prodloužená doba
života atomu. Je to způsobeno tím, že elektron
může absorbovat či emitovat foton jen s vhodnou energií
rovnající se rozdílu mezi hladinami (u
Rydbergových elektronů jsou to energie hluboko v infračervené
oblasti). Životnost Rydbergovského atomu
je úměrná n4.
Vysoce excitované
Rydbergovy atomy se při přiblížení mohou navzájem vázat
sdílením elektronů a vytvářet pravidelné uspořádání do
hexagonálních rovinných klastrů, tzv. Rybdergovu
hmotu. Při formování tohoto klastru dochází k
delokalizaci valenčních vysoce excitovaných elektronů a k
jejich zachycení v potenciálových jámách vzniklých mezi
jádry atomů. Toto uvěznění zabraňuje elektronům opustit
klastr a způsobuje dlouhou životnost
Rydbergovy hmoty. Další vlastností je značně slabá
interakce této hmoty s elektromagnetickým zářením -
její "temnost". Tyto vlastnosti dělají z
Rydbergovy hmoty určitého kandidáta na temnou hmotu
ve vesmíru, nebo na nějakou její část (§5.6, část "Budoucí
vývoj vesmíru. Temná hmota"
v knize "Gravitace, černé díry ....).
Deexcitace
atomů
K dexcitaci atomu a emisi záření již pak
dochází většinou samovolně (podle některých koncepcí kvantové teorie pole je
spontánní deexcitace a emise záření iniciovaná
neustálými kvantovými fluktuacemi vakua). Elektrony mohou v atomech přecházet pouze mezi
existujícími diskrétními energetickými hladinami.
I zde však existují určitá omezení,
způsobená zákonem zachování momentu hybnosti. Foton
odnáší uvolněný rozdíl momentu hybnosti mezi
příslušnými hladinami prostřednictvím svého spinu,
který je roven 1. Přechod mezi hladinami,
jejichž moment hybnosti se liší např. o 1/2, není tedy
fotonovou deexcitací možný - říkáme že tento přechod je
"zakázaný". Obsadí-li elektron
takovou vyšší energetickou hladinu, nemůže samovolně
přejít do nižšího (základního) energetického stavu -
zůstává dlouhodobě "uvězněn" na vyšší
hladině: takový stav se nazývá metastabilní,
či izomerní (atomy, které
uvízly v metastabilním stavu se od původních atomů liší
jen energetickým stavem). Deexcitace
může být vyvolána buď Coulombicky (neradiačně) interakcí
s okolními atomy či částicemi, nebo přes vyšší hladinu
radiačně.
S podobným mechanismem "dovolených"
a "zakázaných" přechodů - gama-deexcitací
- se setkáme i v atomovém jádře v §1.2,
část "Záření gama",
pasáž "Jaderná izomerie
a metastabilita".
Metastabilní stavy atomů se využívají
v některých radiačních aplikacích :
- Kvantové generátory světla - LASERy
pomocí ozáření světlem "čerpají" elektrony do
metastabilních hladin a rovněž pomocí světla spouštějí
hromadný zpětný přechod, lavinovitou deexcitaci,
vedoucí k intenzívnímu světelnému záblesku.
- Termoluminiscenční dozimetry, v jejichž
citlivé látce se elektrony vlivem expozice ionizujícím
zářením excitují do metastabilního stavu a při pozdějším
vyhodnocení je deexcitace vyvolána ohřevem (§2.2 "Fotografická
detekce ionizujícího záření",
pasáž "Termoluminiscenční dozimetry").
Samotný proces deexcitace vzbuzené
energetické hladiny a formování vyzářeného fotonu je velmi
rychlý, avšak ne okamžitý. Podle zákonitostí kvantové
elektrodynamiky proces deexcitace elektronu v atomovém obalu
činí cca 10-16 s.
Ionizace
atomů
Pokud je atomu či některému jeho elektronu dodána
energie vyšší než vazbová energie elektronu
na určité energetické hladině, uvolní se
tento elektron a vyletí z atomu - dojde k ionizaci
atomu, z něhož se stává iont (řec. ión=poutník, jdoucí). Při vyražení elektronu se z neutrálního atomu
stane kladně nabitá částice, kationt. Je-li v okolí
dostatek elektronů, dojde k opětovnému záchytu elektronu - k rekombinaci
elektronu s iontem, za vzniku neutrálního atomu a fotonového
vyzáření vazbové energie elektronu. Podobně může být
neutrálnímu atomu předán elektron "navíc" (v
elektrickém výboji, jiným atomem); výsledkem je
převládající záporný elektrický náboj, vznikne aniont
(záporný iont).
K ionizaci dochází při nárazech rychle
letících částic - ionizujícího záření - do atomů, dále
v elektických výbojích, při srážkách rychle se
pohybujících atomů v látce zahřáté na vysokou teplotu (několik tisíc stupňů), při
rozpouštění solí ve vodě, při mechanickém tření látek
("statická elektřina"). Jako ionty se mohou chovat i molekuly,
u nichž dojde k nerovnováze elektrického náboje. Kdykoli atom
nebo molekula ztratí nebo získá elektron a počet elektronů
již neodpovídá počtu protonů v jádře, vzniká iont
- atom či molekula nese kladný nebo záporný elektrický
náboj. Atomy a molekuly, které mají jeden či více volných
nebo chybějících elektronů, mají zvýšený sklon k
chemickým reakcím (viz níže "Interakce
atomů") vlivem k elektrických interakcí s dalšími atomy.
Mohou přitom vnikat atomy a molekuly, které jsou sice již
elektricky neutrální (mají stejný
počet protonů a obíhajícch elektronů, nejsou tedy ionty), ale mají na svých orbitech nespárované elektrony:
označují se jako radikály, protože
jsou chemicky velmi reraktivní, mezi sebou i s
dalšími okolními atomy a molekulami (jejich
zásadní význam pro radiační účinky na hmotu a živou
tkáň je podrobněji rozebírán v kap.5 "Biologické účinky ionizujícího záření").
Emitované
záření
Energie vyzařovaných fotonů je dána energetickým rozdílem
mezi hladinami elektronů v atomu. Energetické rozložení
elektronových hladin je pro atomy daného prvku zcela charakteristické,
takže změřením spektra vysílaného určitou látku můžeme
stanovit prvek, jehož atomy se tam nacházejí - to tvoří
náplň atomové spektrometrie.
Spektrální
rozložení vlnových délek, resp. fekvencí či energií
fotonů elektromagnetického záření vysílaného látkami
může mít v krajních případech sva diametrálně odlišné
tvary :
Z hlediska pozičního vztahu mezi primárním zdrojem energie, zářícími atomy a spektrometrem se setkáváme se dvěma druhy spekter :
Interakce
atomů
Atomová struktura hmoty
umožňuje přirozeně a z jednotného fyzikálního hlediska
vysvětlit řadu důležitých jevů na atomární a
subatomární úrovni, od nichž se odvíjí všechny vlastnosti
a projevy hmoty - chemické reakce a vlastnosti molekul, stavba a
vlastnosti pevných, kapalných a plynných látek, pružnost a
pevnost, všechny tepelné jevy (kinetická teorie tepla),
elektrické, magnetické a optické vlastnosti látek.
Chemické
slučování atomů - molekuly
Každý atom do svého elektronového obalu naváže počet
elektronů přesně rovný počtu protonů, aby byl atom elektricky
neutrální. Tato elektrická neutralita atomů se však
plně projevuje pouze ve větších vzdálenostech, kde pole
kladně nabitého jádra je dokonale "odstíněno"
zápornými elektrony v obalu. V těsné blízkosti atomu se ale
můžeme setkat se zbytkovými projevy elektrických sil
*), způsobenými vektorovým skládáním intenzit elektrického
pole od protonů v jádře a od elektronů nacházejících se v
různých místech elektronové konfigurace obalu. Při těsném
přiblížení dvou atomů mohou tyto elektrické síly vést k
takovému přeskupení konfigurace elektronů na vnějších
slupkách (např. ke sdílení nebo předání elektronů), že
mohou vzniknout elektrické přitažlivé síly,
které trvale svážou atomy k sobě - vznikne molekula.
Říkáme že došlo k chemickému sloučení
atomů. Kombinací přeskupených elektronových orbitalů
jednotlivých atomů vznikají společné molekulové
orbitaly. Z energetického hlediska při chemické vazbě
dochází k takovému přeskupení elektronů (elektronové
hustoty) ve vnějších valenčních vrstvách blízkých atomů,
které má nižší energii než izolované
atomy, a proto je stabilnější.
*) Je zajímavé, že ačkoli elektrické
síly mají dlouhý (neomezený) dosah, jejich "zbytkový
projev" - "chemické" síly mezi atomy - jsou krátkodosahové.
Při vektorovém skládání elektrických sil od protonů v
jádře a elektronů v obale se ve větších vzdálenostech tyto
síly ruší, avšak v krátkých vzdálenostech zůstává
nenulový "zbytek". S podobným mechanismem se
setkáváme i v atomovém jádře u krátkodosahových jaderných
sil mezi nukleony, které jsou zbytkovým projevem
dlouhodosahových silných interakcí mezi kvarky - viz níže
"Stavba
jádra", část "Silné
jaderné interakce".
V důsledku
energie, uvolněné při chemické vazbě atomů, vznikají
molekuly v energeticky excitovaném stavu.
Deexcitace nastává buď vyzařováním kvant infračerveného
záření, nebo přímou elektromagnetickou interakcí s
okolními atomy a molekulami. Radiační deexcitace se uplatňuje
při reakcích v řídkém plynném prostředí, zatímco v
hustém prostředí kapalin a pevných látek je dominantní
přímá dexcitace za účasti okolních atomů a molekul. V obou
případech se nakonec energie uvolněná při chemickém
sloučení přenese na okolní atomy a molekuly látky ve formě kinetické
energie jejich pohybu - látka se zahřívá,
vzniká reakční teplo (máme zde na mysli
reakce exotermické, viz níže).
Při vzájemném přibližování atomů dochází zpočátku
k jejich elektrickému odpuzování (souhlasně
nabité elektrony v obalech). K dostatečnému přiblížení
atomů - takovému, aby došlo k prolnutí jejich orbitalů a
mohla vzniknout chemická vazba - musí být tedy překonána
určitá elektrická odpudivá bariéra. Atomům
musí být dodána příslušná aktivační energie.
To se děje kinetickou energií tepelného pohybu atomů - k
uskutečnění chemických reakcí je zapotřebí určitá
minimální teplota reakční směsi. Za
nízkých teplot chemické reakce neprobíhají *). Při
vysokých teplotách látky sice dochází k rychlejšímu
průběhu chemických reakcí, avšak střední kinetická
energie atomů a molekul může převýšit vazbovou energii
atomů v molekulách - při srážkách dochází k rozbití
molekul, k rozkladu chemické sloučeniny.
*) Další možností stimulace chemických
reakcí je ozáření ionizujícím zářením. V ozářené
látce se z atomů uvolňují elektrony a vznikají kladné
ionty. Vzniklé elektrické síly umožňují slučování atomů
bez nutnosti udělení kinetické energie pro překonání
odpudivých sil. Radiační stimulace chemických reakcí hraje
významnou úlohu v chladných plyno-prachových oblacích ve
vesmíru (viz "Kosmické
záření"). Avšak na již
"hotové" molekuly působí ionizace zářením
rozkladně - dochází k radiolýze sloučenin.
Zatím neprobádanou možností chemických reakcí za nízkých
teplot je vzájemný průnik vlnových funkcí atomů tunelovým
jevem.
Energie a
kinetika chemických reakcí
Jak bylo shora zmíněno, pro uskutečnění sloučení dvou
atomů je třeba jim dodat určitou aktivační kinetickou
energii QA.
Při vlastním sloučení se naopak uvolňuje vazbová energie
atomů v molekule QR. Z hlediska energetické bilance je důležitý jejich
rozdíl Q = QR-QA - energie reakce. Podle znaménka
energie reakce se chemické reakce dělí na dvě skupiny :
¨
Endotermické (endoenergetické) reakce Q<0,
kde vazbová energie atomů v molekule je menší než kinetická
energie interagujících atomů, "spotřebovaná" na
překonání odpudivých elektrických sil. Endotermické reakce
se nemohou udržovat samovolně, aktivační energii je třeba
nepřetržitě dodávat zvenčí; rychlost takových reakcí je
pak dána "přísunem" této energie. Příkladem je
vznik siruohlíku při průchodu par síry přes rozžhavený
uklík: C + 2 S ® CS2.
¨
Exotermické (exoenergické) reakce Q>0,
kde dochází k "uvolňování" a zisku energie, která
se čerpá z vazbové energie atomů v
molekulách. U exotermických reakcí je několik možností
jejich kinetiky. Časový průběh - kinetika
exotermické reakce - rozhodujícím způsobem závisí na
koncentraci interagujících atomů v reakční směsi, na tlaku,
teplotě, přítomnosti jiných druhů atomů či molekul.
Při dostatečně
vysoké koncentraci reagujících atomů může nastat situace,
kdy uvolněná reakční energie při sloučení dvou atomů je
elektromagnetickou interakcí účinně předána okolním
atomům. Tyto atomy tím získají kinetickou energii,
způsobující jejich okamžité sloučení, čímž se uvolní
další energie - ta se předá dál a způsobí sloučení
dalších atomů. Po dodání počáteční (iniciační)
aktivační energie tak vzniká řetězová chemická
reakce *). Pokud je v reakční směsi obsaženo velké
množství atomů v dostatečně vysoké koncentraci, má tato
řetězová reakce charakter exploze: její
rychlost exponenciálně narůstá, během nepatrného okamžiku
(řádu ms) se prakticky všechny atomy v reakční směsi
sloučí. Náhle uvolněné reakční teplo zahřeje směs na
vysokou teplotu (řádově tisíců stupňů), což způsobí
prudkou expanzi - výbuch reakční směsi.
Známým příkladem je zapálení směsi vodíku s kyslíkem,
stačí maličká jiskra lokálně zvýšené teploty. Pokud je
koncentrace jedné ze složek nižší, nebo jednotlivé složky
jsou do reakčního prostoru přiváděny postupně, může se
ustavit rovnovážná řetezová reakce, mající
charakter plynulého hoření.
*) Podobnou kinetiku, ale poněkud jiný
mechanismus, má jaderná řetězová reakce
štěpení těžkých jader uranu či plutonia působením
neutronů - viz §1.3, část "Štěpení atomových jader".
Při nízkých
koncentracích reagujících atomů řetězová reakce nenastane.
Při sloučení atomů v molekulu se sice uvolní vazbová
energie, která se vyzáří ve formě fotonů infračerveného
záření. Tyto fotony však odletí pryč, pravděpodobnost
jejich absorbce jinými vzdálenými atomy v řídkém
prostředí je nepatrná. Pro probíhání chemických reakcí v
řídkém prostředí musí být aktivační energie dodávána
zvenčí nepřetržitě (situace je podobná jako u
endotermických reakcí).
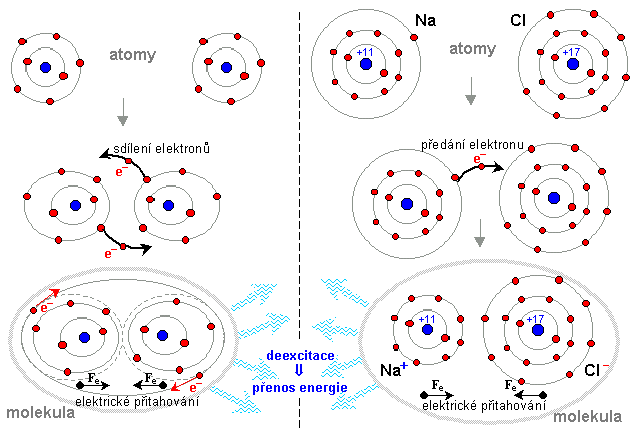
Obr. 1.1.7. Symbolické znázornění mechanismu slučování
atomů a jejich elektrické vazby v molekulách.
Vlevo: Kovalentní vazba dvou atomů způsobená
sdílením elektronů. Vpravo: Iontová vazba
atomů způsobená předáním elektronu jednoho atomu druhému
atomu.
Druhy chemické vazby
Při vzájemném přiblížení dvou atomů mohou nastat v
zásadě tři krajní možnosti jejich interakce :
Kromě zmíněné čistě kovalentní a čistě
iontové vazby dochází v mnoha molekulách ke smíšenému typu
vazby, při níž atomy sdílejí elektrony nestejnou měrou.
.............
Kovová vazba
Vedle kovalentní a iontové vazby mezi dvěma atomy existuje
ještě jiný druh vazby, kdy elektrony vnější valenční
vrstvy nejsou sdíleny dvěma jádry či atomy, ale velkým
množstvím atomů. Toto se uplatňuje v kovech. Atomy kovů se
vyznačují malým počtem elektronů ve vnější slupce,
většinou jeden či dva elektrony. Tyto vnější valenční
elektrony z většího počtu blízkých atomů pak mohou
vytvořit jediný souvislý oblak - tzv. elektronový
plyn, v poli pravidelně rozmístěných jader
obklopených elektrony vnitřních vrstev. Krystal kovu
představuje jakousi obrovskou "molekulu", tvořenou
pravidelně rozloženými kationty, mezi nimiž se volně
pohybují vazebné elektrony. Elektrostatické přitažlivé
síly mezi těmito kationty a elektrony v oblaku pak tvoří
vazbu zvanou kovová.
Z fyzikálního hlediska se chemické vazby popisují pomocí několika parametrů, z nichž zde zmíníme čtyři :
Podobným způsobem jako atomy spolu mohou
dále reagovat i molekuly, či atomy s
molekulami. Podrobnější rozbor mechanismů vazby atomů
patří do oblasti fyzikální chemie.
Slučování konkrétních druhů atomů a vlastnosti vzniklých
molekul (reakce jejich dalšího slučování či rozkladu) pak
tvoří hlavní náplň chemie.
Periodické
chemické vlastnosti atomů
V předvědeckém období se zkoumáním látek zabývali alchymisté.
Ti ovšem neměli potuchy nejen o atomech a jejich jádrech, ale
nerozeznávali ani prvky a sloučeniny. Látky posuzovali podle
jejich vnějších projevů a několika jednoduchých
"lučebných" reakcí, které dokázali uskutečnit. V
18.stol., kdy byly postupně opuštěny dřívější omyly
alchymie a řadou pokusů rozlišovány chemické prvky
a sloučeniny, vznikla klasická chemie,
jakožto věda o slučování prvků, vlastnostech sloučenin,
jejich dalších vzájemných reakcí slučování a rozkladu.
Nejdůležitějším zjištěním byl objev periodicity
vlastností prvků podle jejich relativní atomové váhy (nyní
víme že o tom rozhoduje atomové neboli protonové číslo Z):
jsou-li prvky řazeny postupně podle svého atomového čísla,
jejich chemické vlastnosti se po určité sekvenci prvků
opakují (viz též výše část "Atomová
struktura hmoty", pasáž
"Periodická tabulka prvků").
Systematickým vyvrcholením klasické chemie bylo vytvoření periodické
tabulky prvků (Mendělejev její první verzi sestavil
v r. 1869), ve které jsou prvky řazeny podle stoupajícího
atomového čísla do vodorovných řad (tvořících periody)
tak, aby se prvky podobných vlastností dostaly pod sebe (do
sloupců). Mendělejev ponechal v tabulce několik prázdných
míst a vyslovil odvážnou hypotézu, že později budou
objeveny nové prvky, které tyto mezery zaplní; to se opravdu
splnilo.
V první polovině
20.stol. bylo odhaleno, že periodicita prvků má základ v
kvantovém chování elektronů obíhajících kolem atomového
jádra, v zákonitostech obsazování
jednotlivých orbitalů (bylo vysvětleno
výše v části "Planerární a Bohrův model atomu", pasáž "Obsazování a
konfigurace elektronových hladin").
První perioda má pouze
jeden typ orbitalu zvaný "s", který může být
obsazen jedním (u vodíku) nebo dvěma (u hélia) elektrony.
Atomy druhé a třetí periody mají vedle jednoho orbitalu
"s" ještě tři orbitaly typu "p". Každý z
těchto 4 orbitalů může být zaplněn opět jedním nebo
dvěma elektrony, s celkovým možným počtem 8 elektronů,
čímž vzniká perioda po osmi prvcích. Čtvrtá a pátá
perioda mají kromě orbitalů "s" a "p"
ještě třetí typ "d", který přidává navíc
dalších 10 míst pro elektrony - délka periody se tím
prodlužuje na 18 prvků. Poslední dva řádky tabulky obsahují
těžké atomy se čtyřmi orbitaly typů
"s","p","d" a "f" a mají
periodu délky 18+14 = 32 prvků. Poslední prvek se Z=118 má
všechny orbitaly "s,p,d,f" zaplněné elektrony. Pokud
se podaří syntetizovat další těžší prvky (supertěžké
transurany - viz §1.3, část "Transurany"), bude pro ně muset být vytvořen zcela nový
řádek tabulky. Od prvku 121 by pak přibyl nový, zatím
neznámý typ orbitalu "g", čímž by se periodicita
(počet sloupců) prodloužila až na 50 prvků. Z hlediska
chemických vlastností atomů to však má jen diskutabilní
význam, supertěžká jádra se okamžitě rozpadají a příp.
jejich prchavé atomy mají jiné vlastnosti než odpovídá
periodické tabulce :
Narušení periodicity
?
Přesná periodicita fyzikálně-chemických vlastností platí
pouze u lehčích prvků. Princip podobného chování prvků ve
stejném sloupci periodické tabulky může být pro těžké
atomy narušen v důsledku relativistických efektů
v elektronovém obalu. Při vysokém počtu protonů je vysoký
elektrický náboj jádra, což vede také k vysoké rychlosti
elektronů na vnitřních orbitalech. U těžkých atomů
vnitřní elektrony dosahují orbitálních rychlostí, které se
částečně přibližují rychlosti světla (stávají se
"relativistické"), takže se zde začínají
uplatňovat efekty speciální teorie relativity. Vlivem
relativistické kontrakce dochází ke zmenšení velikosti
(smrštění) vnitřních orbitalů. Zmenšení poloměru
vnitřních orbitalů má za následek zvýšení elektrického
"stínění" kladného náboje jádra těmito
elektrony, takže vzdálenější elektrony (již
nerelativistické) jsou k jádru přitahovány menší silou.
Vnější orbitaly, především valenční, jsou u těžkých
atomů méně vázány, než by odpovídalo běžnému
nerelativistickému kvantovému modelu atomu. A též energetický
odstup mezi vnějšími hladinami je menší.
Projevuje se to v optických vlastnostech prvků a v některých
specifických chemických reakcích. Relativistické kvantově
mechanické efekty způsobují, že se atomy velmi těžkých
prvků v oblasti transuramů mohou chovat chemicky jinak,
než bychom předpokládali na základě jejich umístění ve
sloupcích Mendělejevovy periodické tabulky (bude diskutováno v §1.3, na konci části "Transurany", v pasáži "Chemické
vlastnosti transuranů").
Vazby
atomů a molekul v pevných a kapalných látkách
Vedle výše zmíněných radiačních jevů a procesů
chemického slučování atomů jsou elektrické síly, dané
elektronovými konfiguracemi atomových obalů, zodpovědné i za
těsné shlukování velkého počtu atomů a molekul do pevných
látek a kapalin, jakož i za jejich
vlastnosti - pružnost, pevnost, stlačitelnost, elektrické,
magnetické a optické vlastnosti, tepelné vlastnosti.
V pevných
látkách se projevují v prvé řadě analogy iontové
a kovalentní vazby, které byly výše
zmíněny v souvislosti s chemickým slučováním atomů na
molekuly. Kromě toho se v kapalinách (a částečně i v
amorfních pevných látkách) uplatňují podstatně slabší
tzv. van der Waalsovy síly.
Van
der Waalsovy síly
Všechny atomy a molekuly (i atomy inertních plynů hélia
argonu, xenonu atd.) vykazují slabé vzájemné přitahování
krátkého dosahu, které je způsobováno tzv. van der
Waalsovými silami *). Základem van der Waalsovy síly
jsou přitažlivé síly mezi elektrickými dipólovými
momenty atomů nebo molekul. U polárních molekul,
které mají permanentní elektrický dipólový moment (jako je
molekula H2O,
kde konec molekuly s atomem kyslíku má větší koncentraci
elektronů a je zápornější než opačná část molekuly s
vodíkovými atomy), se molekuly k sobě navzájem orientují
svými konci opačné polarity, přičemž vzniká přitažlivá
elektrická síla.
*) Tyto přitažlivé "kohesní" síly (síly
soudržnosti) mezi molekulami zavedl na základě
fenomenologických úvah v r.1873 J.D. van der Waals do své
známé stavové rovnice nedokonalého (tj.
reálného) plynu, zobecňující stavovou rovnici pro dokonalé
plyny, aby bylo možno vysvětlit kondenzaci
plynů.
Polární
molekula může ale přitahovat i molekuly, které normálně
nemají permanentní dipólový moment: elektrické pole
polární molekuly při přiblížení způsobí takové
přerozdělení náboje ve druhé molekule, že se v ní indukuje
dipólový elektrický moment ve stejném směru jako je moment
polární molekuly - výsledkem je přitažlivá síla.
Podrobnější elektrický rozbor ukazuje, že velikost této
síly FW ~ a.d2/r7 je úměrná čtverci dipólového momentu d a
nepřímo úměrná 7.mocnině vzdálenosti r ; a je konstanta
udávající polarizovatelnost molekuly..
Avšak i u nepolárních molekul a u atomů s uzavřenými
slupkami, kde je rozdělení elektronů v průměru symetrické a
střední dipólový moment d je nulový, okamžitý
dipólový moment vykazuje kvantové fluktuace co do velikosti a
směru. I když střední hodnota dipólového momentu <d> je nulová,
střední hodnota čtverce dipólového momentu <d2> není nulová, ale má malou konečnou hodnotu -
vzniká tím efektivní přitažlivá síla mezi oběma
fluktuujícími elektrickými dipólovými momenty, která je
úměrná ~<d2>/r7.
Van der Waalsovy síly jsou mnohem slabší než síly
iontových a kovalentních vazeb. Navíc vysoká mocnina jejich
nepřímé závislosti na vzdálenosti, r -7, způsobuje, že se
jedná o síly krátkého dosahu, které se
uplatňují jen když jsou molekuly či atomy těsně u sebe
(zdvojnásobení vzdálenosti mezi dvěma molekulami sníží
přitažlivou sílu působící mezi nimi více než 120-krát).
Van der Waalsovy síly způsobují kondenzaci plynů na
kapaliny a tuhnutí kapalin na pevné látky i tehdy, když se
mechanismus iontové nebo kovalentní vazby neuplatňuje (např.
u inertních atomů s uzavřenými slupkami). Tyto síly jsou
též základem dalších vlastností látek, jako je viskozita,
povrchové napětí, adheze, tření.
Podle skupenství dělíme
látky na známé tři základní skupiny :
Tepelné
pohyby atomů a molekul
Atomy a molekuly, tvořící látky, nejsou nikdy vzájemně v
klidu, ale vykonávají neustálé pohyby. Podle kinetické
teorie tepla jsou právě pohyby atomů a molekul v
látkách příčinou a podstatou všech tepelných jevů. V
pevných látkách vykazují atomy a molekuly kmitavý
pohyb v krystalové mřížce. V plynech a kapalinách
probíhá neuspořádaný pohyb pružně se
srážejících *) atomů a molekul (může být pozorován jako
známý Brownův pohyb).
*) Při dostatečně vysokých teplotách
však již tyto srážky atomů a molekul nejsou pružné,
dochází k excitaci atomů a molekul s
následnou deexcitací doprovázenou zářením. Při ještě
vyšších teplotách pak dochází k ionizaci
atomů a rozkladu molekul, vzniká plasmatický
stav, nazývaný někdy 4.skupenství (viz níže
pasáž "Plasma-
4.skupenství hmoty")...
Mechanické nárazy atomů a molekul plynu na
stěny nádoby vyvolávají síly reakce, které jsou příčinou
tlaku plynu.
Okamžitá rychlost jednotlivých srážejících se molekul
plynu je různá a s časem se nepravidelně mění jak co do
velikosti, tak co do směru. Ve statistické mechanice se
odvozuje tzv. Maxwellův-Boltzmannův zákon
statistického rozdělení kinetických energií pohybujících
se molekul v (ideálním) plynu ........ . V plynu zahřátém na
(absolutní) teplotu T je střední kinetická energie <ek> na jednu
molekulu úměrná teplotě podle vztahu: <ek> = (3/2).k.T,
kde k je tzv. Boltzmannova konstanta,
jejíž číselná hodnota je k = 1,380.10-23 Joule/Kelvin. Tato konstanta je jakýmsi
"přepočítávacím faktorem" mezi energetickou
mírou teploty látky a fenomenologicky zavedenou teplotní
stupnicí ve stupních Kelvina (°K; vztah mezi
absolutní Kelvinovou stupnicí a "vodní" Celsiovou
stupnicí je T[°K] = 273 + t[°C] ).
Jelikož kinetická energie ek molekuly o hmotnosti m
souvisí s její rychlostí v známým vztahem ek = (1/2)mv2, vychází pro rychlost molekul (tzv. střední
kvadratickou rychlost <vkv> - je druhou
odmocninou ze střední hodnoty čtverce rychlosti molekul)
vztah: <vkv> = Ö<v2> = Ö(3kT/m). Pro běžné plyny za teplot obvyklých v
zemském ovzduší jsou tyto rychlosti řádu stovek metrů za
sekundu. Např. pro vodík za teploty 0°C (= 273°K) je <vkv> » 1300 m/s.
Mechanické nárazy atomů a molekul na stěny nádoby
vyvolávají síly reakce, které jsou příčinou tlaku
plynu. Tlak P se vyjadřuje jako síla působící na
jednotku plochy, přičemž tato síla je dána rychlostí
časové změny hybnosti dopadajících
částic. Hybnost p = m.v
molekuly hmotnosti m souvisí s její kinetickou energií
vztahem ek = p2/m. Při každém
pružném nárazu na stěnu změní molekula svoji hybnost na
opačnou, tj. celková změna její hybnosti je Dp = 2.p. Hybnosti
částic jsou orientovány chaoticky do všech tří směrů v
prostoru, takže počet částic dopadajících na stěnu činí
v průměru jen 1/3 celkového jejich počtu. Počet
dopadajících částic je dále dán jejich počtem no v objemové jednotce.
Po započtení všech těchto okolností je tlak daný vztahem: P
= (1/3).m.no.<v2>, resp. P = (1/3).r.<v2>, kde r je hustota plynu. Tlak plynu na stěny nádoby je tedy
přímo úměrný hustotě plynu a střední hodnotě čtverce
rychlostí jeho molekul.
............stavová rovnice....
...................
Šíření tepla
Teplo, tj. neuspořádané či kmitavé pohyby atomů a molekul,
se v látkách šíří z jednoho místa na
druhé třemi základními způsoby :
Pro tepelné vlastnosti látek je důležitá
závislost mezi pohlceným množstvím tepla (energie) DQ a vzrůstem
teploty DT zahřívaného tělesa o hmotnosti m. Tato
závislost má obecně složitý nelineární průběh, avšak
pokud nedochází k fázovým přechodům (změnám skupenství)
a nepohybujeme se ve velkém rozmezí teplot (v limitě DT®0), je tato
závislost přibližně lineární: DQ = m.C.DT. Koeficient C
v této závislosti se nazývá specifické či měrné
teplo dané látky.
...................
..............
Podrobnější studium tepelné energie a teplotních vlastností
látek tvoří náplň speciální oblasti fyziky - termiky
a termodynamiky.
Elektromagnetické
a optické vlastnosti látek
Atomová a molekulová struktura hmoty umožňuje přirozeně a z
jednotného fyzikálního hlediska vysvětlit interakce
elektrického a magnetického pole, elektromagnetického vlnění
(a speciálně světla), s látkami. Právě ze základních
stavebních částic atomu - elektronů,
jakožto nositelů elementárního záporného elektrického
náboje, a protonů nesoucích kladný
elementární náboj - pramení veškeré elektrické a
magnetické jevy. A silová působení - interakce -
elektrických a magnetických polí s atomy a molekulami
látkového prostředí způsobují všechny zvláštnosti a
rozdílnosti elektromagnetických jevů ve srovnání s těmito
jevy ve vakuu. Níže bude ukázáno, že z makroskopického
hlediska lze elektromagnetické pole v látkovém prostředí
(především v dielektrickém) v zásadě popsat stejnými
Maxwellovými rovnicemi jako ve vakuu, v nichž jsou hodnoty
elektrické permitivity eo a magnetické
permeability mo vakua nahrazeny
příslušnými koeficienty e a m pro danou látku.
Z obecného teoretického
hlediska je to diskutováno v §1.5 "Elektromagnetické
pole. Maxwellovy rovnice"
knihy "Gravitace, černé díry a fyzika prostoročasu".
Elektrické
jevy v látkovém prostředí
Na základě vlastností atomů a molekul lze především
vysvětlit elektrostatické jevy, včetně
samotného "vzniku" elektrického náboje. Při
interakcích atomů a molekul v látkách (v nejjednodušším
případě při mechanickém tření dvou těles) může
docházet k uvolňování určitého počtu vnějších
elektronů z atomů. Shromáždí-li se větší počet těchto
elektronů na jednom z interagujících těles, vykazuje toto
těleso s přebytkem elektronů záporný elektrický náboj,
zatímco u druhého tělesa s přebytkem protonů se uplatňuje
kladný elektrický náboj. Takováto elektricky nabitá
tělesa o náboji Q1 a Q2, umístěná ve vakuu ve vzdálenosti r, na sebe
budou silově působit podle známého Coulombova zákona
F = k . Q1.Q2/r2, kde k je koeficient vyjadřovaný v soustavě
jednotek SI pomocí tzv. permitivity vakua eo: k = 1/4peo.
Jsou-li elektricky nabitá tělesa umístěna v látkovém
prostředí, vedle jejich vzájemného Coulombovského
působení bude docházet i k jejich elektrickým interakcím s
atomy a molekulami látky. Základní charakter této interakce
bude záviset především na té okolnosti, zda jsou nebo nejsou
v látce obsaženy volně pohyblivé nosiče
elektrického náboje.
Fyzika pevných látek
popisuje elektrické vlastnosti těchto látek pomocí tzv. pásové
teorie, podle které jsou elektrony v látce sdruženy
do energetických pásů, navzájem oddělených neobsazenými
pásy "zakázaných" energií. Diskrétní energetické
stavy elektronů obíhajících kolem jednotlivých atomů v
pevných látkách na orbitálních drahách se vlivem interakce
s dalšími atomy v pevné látce rozšiřují do energetických
pásů, přičemž však mezi těmito pásy zůstávají
určité mezery - tzv. pásy zakázaných energií,
které elektrony nemohou nabývat. Energeticky nejvýše
položený obsazený pás je pás valenční,
následuje zakázaný pás a nad ním leží tzv. vodivostní
pás elektronů, které se již chovají jako volné.
Je-li zakázaný pás široký, je v rovnovážném (základním)
stavu vodivostní pás zcela neobsazen, všechny
elektrony jsou vázané a látka je elektricky nevodivá. V opačném případě do
vodivostního pásu přeskakující elektrony způsobují elektrickou
vodivost látky.
Z tohoto elektrického hlediska se tedy
látky rozdělují na dvě krajní skupiny :
1. Vodiče
- látky které obsahují volně pohyblivé elektrické náboje
(resp. jejich nosiče). Elektrické pole svými silovými
účinky uvede nosiče elektrického náboje do pohybu
- vznikne elektrický proud, který trvá tak
dlouho, dokud přeskupené elektrické náboje nevyruší
elektrické pole; náboje se vyrovnají. Podle charakteru
pohyblivých nosičů elektrického náboje se elektrická
vodivost rozděluje na dva druhy :
-> Elektronová vodivost
způsobená volně pohyblivými elektrony. Vodivostní pás je
natolik blízko, že se překrývá s pásem valenčním a
vnější elektrony volně přecházejí do vodivostního pásu.
Vyskytuje se především v kovech, kde část
vnějších elektronů není vázána v atomech v krystalové
mřížce, ale je volně rozptýlena a tvoří tzv. elektronový
plyn. Kovy jsou proto velmi dobrými vodiči elektrického
proudu a též tepla. Zajímavou vlastností těles z vodivého
materiálu je tzv. skin-efekt - když se toto vodivé
těleso nabije, elektrický náboj se shromáždí pouze na povrchu
a dovnitř nepronikne; a v příp. dutině uvnitř nebude
působit elektrické pole. Tento jev se využívá pro
elektrické stínění - viz níže "Faradayova klec".
Velké
množství slabě vázaných elektronů ve vodivostním pásu
kovů umožňuje poměrně snadné uvolnění elektronů
z jejich povrchu. Zahřátí kovu (na
teplotu nad cca 400°C) zvýšením
kinetické energie elektronů způsobuje termoemisi
elektronů. Podobně dopad elektromagnetického
záření, světla a tvrdšího záření, vede k fotoemisi
elektronů - fotoelektrický jev (byl
podrobněji analyzován výše v části "Korpuskulárně-vlnový
dualismus", pasáž "Fotoelektrický
jev").
-> Iontová vodivost
způsobená pohybem kladně či záporně nabitých iontů -
atomů s chybějícími či nadbytečnými elektrony v obalu.
Tento druh vodivosti se vyskytuje v roztocích s
disociovanými molekulami - tzv. elektrolytech,
nebo v ionizovaných plynech (elektrické
výboje).
Pohyb elektrických nábojů ve vodičích není
zcela volný, nosiče elektrického náboje narážejí na atomy
a molekuly v látce, čímž jim předávají část své
elektricky získané kinetické energie. Elektrický proud
vytváří teplo, vodiče kladou elektrickému proudu odpor
(vyjadřuje se v Ohmech). Jedinou výjimkou je jev tzv. supravodivosti,
kdy elektrony (spojené v tzv. Cooperovy
páry vytvářející Bose-Einsteinův kondenzát) se ve vodiči pohybují zcela volně a elektrický
odpor poklesne na nulu (§1.5, pasáž
"Fermiony v úloze bosonů;
Supravodivost").
-> Polovodivost. Zvláštní
skupinou látek jsou polovodiče, látky s
úzkým zakázaným pásem, kde elektrony
přeskakující z valenčního do vodivostního pásma (tepelným
pohybem či fotoexcitací) se stávají zápornými nosiči
vodivosti a prázdná místa ve valenčním pásu - tzv. díry
- se efektivně jeví jako kladné nosiče vodivosti. Zanesením vhodných
příměsí prvků, které poskytují vodivostní
elektrony (donory), nebo přijímají elektrony z vazeb
valenčního pásu (akceptory) do polovodičových
materiálů, lze dosáhnout zvýšení jejich vodivosti
a převahy volných nosičů záporných ("n") nebo
kladných ("p"). Velmi důležité elektrické jevy
vznikají na rozhraní k sobě přiložených
polovodičů typu "n" a "p" - usměrňovací
"diodový" efekt na rozhraní n-p,
zesilující "tranzistorový" efekt na
rozhraní p-n-p nebo n-p-n, dále jevy optoelektrické.
Nejdůležitějšími polovodičovými materiály jsou germanium
a křemík.
Vedle
širokého použití v elektronice (tranzistory,
diody, LED, integrované obvody, počítačové procesory,
paměťové čipy, optoelektrické zobrazovací čipy, ...) se germanium a křemík používá i v polovodičových
detektorech ionizujícího záření (§2.5 "Polovodičové detektory"). Pro některé účely se
zde používá i kombinace teluru, kadmia a zinku - CZT
detektory.
2. Nevodiče
(izolanty, izolátory, dielektrika)
- látky v nichž nejsou přítomny volně pohyblivé elektrické
náboje (vodivostní pás je od
valenčního oddělen širokým pásem zakázaných energií,
takže se do něj elektrony z atomů nedostávají). Zde může elektrický náboj vložených těles
přetrvávat, nevodivá látka je schopna oddělovat od sebe (izolovat)
náboje různých velikostí a znamének. Atomy a molekuly
zůstávají celkově elektricky neutrální, avšak silovým
působením elektrického pole dochází k určitému
přeskupování rozdělení náboje v atomech a molekulách - k
tzv. polarizaci dielektrika (obr.1.1.8 vpravo).
Původně prostorově v časovém průměru symetrické
rozložení náboje *) se vlivem elektrických sil mírně
zdeformuje - kladný náboj se efektivně posune ve směru pole,
záporný náboj ve směru opačném. Vzniká efekt tzv. posuvných
nábojů.
*) Toto platí pro atomy a tzv. nepolární
molekuly se symetrickým prostorovýn rozložením kladných a
záporných nábojů. Kromě toho existují molekuly polární,
v nichž atomy jsou vázány iontovými vazbami, s nesymetrickým
rozložením náboje tvořícím miniaturní elektrický dipól.
Orientace těchto molekulových elektrických dipólů je ale v
látce vlivem tepelných pohybů zcela neuspořádaná, takže se
jejich elektrické účinky navenek ruší (obr.1.1.8
uprostřed). Vnější elektrické pole však silově působí na
jednotlivé dipóly a částečně je orientuje ve směru pole -
dochází k orientační polarizaci dielektrika
(obr.1.1.8 vpravo). Kromě toho silové působení pole ještě
poněkud zvětší dipólový moment takto orientovaných
polárních molekul.
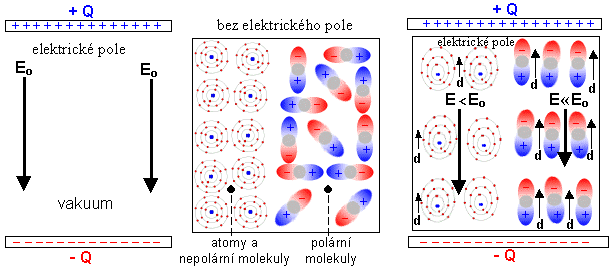
Obr.1.1.8. Polarizace atomů a molekul dielektrika a vznik
posuvných nábojů.
Vlevo: Elektrické
pole mezi dvěma elektrodami o náboji +Q a -Q má ve vakuu
intenzitu Eo. Uprostřed: Bez
přítomnosti vnějšího elektrického pole mají atomy a
nepolární molekuly v průměru symetrické rozložení náboje
a polární molekuly mají náhodné chaotické orientace svých
dipólových momentů. Vpravo:
Působením vnějšího elektrického pole se deformuje původně
symetrické rozložení náboje v atomech a nepolárních
molekulách - stávají se z nich elektrické dipóly; u
polárních molekul dochází k orientaci dipólových momentů.
V obou případech jsou dipólové momenty orientovány
protisměrně vzhledem k vektoru elektrické intenzity Eo
vnějšího pole - polarizace dielektrika efektivně snižuje
intenzitu působícího pole z maximální vakuové hodnoty Eo na
hodnotu E.
Výsledkem elektrické interakce s atomy a molekulami (nepolárními i polárními) dielektrika je vznik elektrických dipólů orientovaných ve směru pole. Elektrické pole takto indukovaných elektrických dipólů d se skládá s původním působícím polem Eo - a jelikož je opačného směru, efektivně zmenšuje hodnotu intenzity elektrického pole, snižuje elektrickou sílu na hodnotu E<Eo. Pro nepříliš silná elektrická pole je polarizace P přímo úměrná intenzitě elektrického pole: P = k.E, kde koeficient k se nazývá dielektrická sucseptibilita (polarizovatelnost) dielektrika. Pro silové působení elektrických nábojů v látce pak platí i nadále Coulombův zákon, avšak v konstantě úměrnosti místo permitivity vakua eo vystupuje permitivita látky e, zvaná též dielektrická konstanta: e = eo+k = er.eo, kde er=1+k je tzv. relativní permitivita látky. Relativní permitivita látek je vždy větší než 1, u nepolárních a řídkých látek jen nepatrně (pro vzduch jen 1,006), u polárních látek může být značně vysoká (pro vodu je er=81).
Magnetické jevy v látkovém
prostředí
Magnetické jevy jsou projevem interakcí pohybujících se
elektrických nábojů. Pohybující se náboje, vytvářející
v délkovém elementu dl proud I,
vzbuzují ve vzdálenosti r magnetické pole o intenzitě B
*) podle Biot-Savart-Laplaceova zákona: dB
= k . I .[dl´ro]/r2, kde ro je jednotkový směrový vektor od měřeného místa k
proudovému elementu a k je konstanta úměrnosti
vyjadřovaná v soustavě jednotek SI pomocí tzv. permeability
vakua mo: k = mo/4p. Magnetické pole pak vykazuje silové účinky na
každý elektrický náboj q pohybující se rychlostí v:
F = q.[B´v]; tato
tzv. Lorentzova síla působí kolmo na směr pohybu
náboje.
*) Veličina B se z
historických důvodů nazývá nikoli intenzita, ale magnetická
indukce.
Buzení
magnetického pole v látkovém prostředí lze opět vyjádřit
pomocí Biot-Savart-Laplaceova zákona, avšak v
konstantě úměrnosti místo permeability vakua mo vystupuje magnetická permeabilita látky
m = mr.mo, kde mr = m/mo je tzv. relativní
permeabilita látky, udávající "zesilující"
či "zeslabující" efekt látky na magnetické pole. Význam slova "permeabilita" je
"propustnost, prostupnost" - zde pro
magnetické pole.
Pro diamagnetické látky je mr<1, pro
paramagnetické látky je mr>1; v obou těchto
případech je však hodnota mr velmi blízká 1. Pro
ferromagnetické látky však dosahuje mr vysokých hodnot řádově 103-105 (zde to však není konstanta,
ale proměnná veličina, jejíž hodnota závisí na intenzitě
magnetického pole; pro silná pole se dosahuje stavu nsasycení
magnetizace, dále se projevuje efekt hysterese - viz níže).
Vložíme-li látku do magnetického pole, bude
docházet k interakcím atomů a molekul látky s magnetickým
polem, vedoucí k magnetizaci látky. Elektrony
pohybující se v atomových obalech totiž vytvářejí své elementární
elektrické proudy ("proudové smyčky"),
vzbuzující svá elementární magnetická pole vyjádřená
tzv. magnetickým momentem m = I.S,
definovaným jako součin proudu I a plochy S
proudové smyčky. V atomech jsou elementární proudové smyčky
a magnetické momenty způsobeny dvěma druhy pohybu elektronů :
a) Oběhem elektronu po jeho dráze - dráhový či orbitální
magnetický moment; b) V
důsledku spinu elektronu - spinový magnetický moment.
Výsledný magnetický moment atomu je vektorovým součtem
momentů všech jeho elektronů. Při tomto vektorovém
sčítání mohou nastat tři význačné případy :
1.
Diamagnetismus
Všechny momenty se navzájem kompenzují, výsledný
moment je nulový. V takovýchto atomech se při
vložení do magnetického pole deformují dráhy elektronů tak,
že se indukují přídavné magnetické momenty,
jejichž pole směřuje (v souvislosti s
tzv. Lencovým pravidlem opačného účinku) proti směru vnějšího pole.
Dochází tedy k zeslabení pole, takové látky
se nazývají diamagnetické. Je to
např. uhlík, měď, síra, voda, zlato, plasty a většina
dalších látek.
2.
Paramagnetismus
Kompenzují se pouze spinové momenty. Ve vnějším magnetickém
poli pak dochází ke stáčení magnetických momentů
jednotlivých atomů do směru souhlasného s vnějším polem,
čímž dochází k zesilování výsledného
magnetického pole. Takové látky se nazývají paramagnetické.
Proti tendenci orientace magnetických momentů však působí
tepelný pohyb atomů, který naopak uvádí atomy do stavu
chaotické neuspořádanosti - podle tzv. Curieova zákona
je magnetický zesilovací efekt, magnetická susceptibilita,
nepřímo úměrný absolutní teplotě. Paramagnetické látky
jsou např. hliník, kyslík, vápník, sodík, hořčík,
mangan, baryum, platina ...
3.
Feromagnetismus
Atomy mají nekompenzované spinové momenty (to se vyskytuje u
atomů, které nemají úplně obsazenou některou elektronovou
hladinu). V takovém případě u některých látek může
dojít k tomu, že v určitých malých oblastech dojde ke spontánní
orientaci všech magnetických momentů do jednoho směru -
vznikne tzv. magnetická doména, která je
zmagnetována do nasyceného stavu (velikost těchto domén je
cca 10-6 -10-2 cm). Za normálních
okolností jsou tyto domény v látce náhodně rozloženy a
orientovány, takže jejich magnetizace se ruší. Při vložení
vnějšího magnetického pole se však tyto domény snadno
orientují tak, že vektor jejich magnetizace směřuje ve směru
pole - dochází k celkové magnetizaci látky, která výrazně zesiluje
působící magnetické pole. Takovéto látky s výraznými
magnetickými vlastnostmi se nazývají feromagnetické
(podle železa, které je
nejstarší známou látkou tohoto druhu).
Feromagnetické vlastnosti zanikají při vyšších teplotách,
kdy nastává rozpad domén spontánní magnetizace a látka
nabývá paramagnetických vlastností (příslušná
hraniční teplota, charakteristická pro danou látku, se
nazývá Curieova teplota). Kromě
železa feromagnetické vlastnosti vykazují např. kobalt, nikl,
gadolinium, neodym a některé slitiny kovů, jako je slitina
Al-Ni-Co hliníku, niklu, kobaltu, železa; Sm-Co
samarium-kobalt; Sr-Fe stroncium s železem; železa, niklu,
molybdenu; železa a chromu; železa, neodynu a boru.
Feromagnetické látky jsou především
zmíněné kovy, které jsou elektricky vodivé. V elektronice se
dále uplatňují elektricky nevodivé (resp. s vysokým elektrickým odporem) feromagnetické materiály zvané ferity
(ferimagnetické materiály). Jsou to sloučeniny oxidů feromagnetických prvků
železa se stronciem, manganem, baryem. Používají se
především jako jádra cívek pro vysofrekvenční signály.
Magneticky měkké a tvrdé
feromagnetické látky. Magnetická hysterese. Permanentní
magnety. Magnetický záznam.
Většina feromagnetických materiálů, např. železo bez
legujících přísad, se sice v magnetickém poli zmagnetuje,
ale při odstranění z magnetického pole se atomy v
magnetických doménách vracejí zpět do své původní
konfigurace a materiál magnetické vlastnosti ztrácí
- nazývá se magneticky měkký materiál.
Avšak některé feromagnetické materiály, když
se zmagnetují při vložení do magnetického pole, i po
odstanění tohoto vnějšího magnetického pole si trvale zachovají
své zmagnetování. Část magnetických domén zůstane
zorientovaných do směru magnetického pole. Jeví tzv. magnetickou
hysteresi (řec. hysteresis =
zpoždění) - závislost aktuálního
fyzikálního stavu magnetismu na předchozích reakcích na
hodnotu aplikovaného magnetického pole. Tyto látky se
nazývají magneticky tvrdé. Tyto vlastnosti
má železo-ocel legovaná příměsí uhlíku, některé slitiny
kovů vzácných zemin jako je samarium-kobalt,
neodym-železo-bor ...
Látky vykazující vysokou magnetickou hysteresi (velkou plochu pod hysteresní křivkou) se používají pro přípravu permanentních
magnetů. Vedle vysoce legované oceli jsou to slitiny
samaria-kobaltu, železa-niklu, kobaltu-niklu-hliníku a několik
dalších. Zvláště vysoká intenzita permanentní magnetizace
(cca 1,3 Tesla) se dosahuje u neodymových
magnetů, vyrobených ze slitiny neodymu, železa a boru -
Nd(2)Fe(4)B.
Tenké
vrstvy feromagnetických materiálů se používají v
elektronických záznamových médiích. Magnetické
pásky - zvukové (audio, magnetofonové), obrazové
(video), datové - jsou tvořeny magnetickou vrstvou nanesenou na
plastovém pásku, který se posunuje kolem jádra cívky. Do
této cívky se přivádí elektrický signál, vznikající
magnetické pole zmagnetovává pásek - vzniká magnetický
záznam. Při čtení se nahraný pásek posunuje kolem
čtecí cívky, v níž se indukuje elektrický signál, který
se po zesílení reprodukuje či zpracovává.
Počítačové disky mají
magnetickou vrstvu nanesenou na plastovém nebo hliníkovém
kotouči, který rotuje a v těsné blízkosti magnetického
povrchu se v radiálním směru mezi středem a okrajem pohybuje
nahrávací a čtecí cívka. Nahrávání a čtení se provádí
v soustředných kružnicích.
Feromagnetické vrstvy u záznamových disků nebo
pásků bývají vytvářeny z práškových feritů (Fe2O3,
Cr2O3, ...) s plastovým pojivem, nanášených v mikronové
vrstvě. V poslední době se u počítačových hard-disků
začala používat nová technologie čtecí hlavy,
využívající spinovou závislost rozptylu elektronů
v magnetických vrstvách. Ve
dvou feromagnetických vrstvách, buzených vnějším
elektromagnetickým signálem, se projevuje rozdílná
magnetorezistence *) v závislosti na orientaci spinů
elektronů - efekt zvaný ("obří")magnetorezistence
GMR. Ve čtecí hlavě se používají dvě
feromagnetické vrstvy, oddělené nemagnetickou vrstvou.
Tento GMR senzor k detekci bitů, kterým jsou
přiřazeny logické "0" a "1", používá
opačný směr magnetizace příslušných elementů na
magnetickém záznamovém médiu, který vyvolává změny
elektrické vodivosti (odporu) senzoru. To způsobuje modulaci
elektrického proudu v obvodu připojeného k GMR senzoru, který
se dekóduje a digitalizuje pro vznik výsledné bitové
informace. Nové technolgie umožnily podstatné zvýšení
kapacity hard disků, z původních cca 10 MB na 500 GB a
později i několik TB. Spintronika
se snaží tohoto efektu využít i u počitačových pamětí
MRAM, které by na nové úrovni mohly mít výhody trvalého
uchování informace, jaké bylo dříve u feritových pamětí.
*) Magnetorezistence
je jev pozorovaný ve vícevrstevných strukturách, složených
z tenkých střídajících se feromagnetických a
nemagnetických vrstev. Projevuje se jako
změna elektrického odporu v závislosti na tom, zda jsou
magnetizace sousedních feromagnetických vrstev směrovány
paralelně nebo protisměrně. Odpor je relativně nižší pro
paralelní směrování a vyšší pro antiparalelní orientaci.
Je to způsobeno závislostí rozptylu elektronů na jejich
spinové orientaci.
Počítačová záznamová média
K záznamu velkého množství dat
v počítačové technologii a informatice byla vyvinuta řada
technologií. Pomineme-li některé historické
před-elektronické pokusy o záznam informací, můžeme
postupný vývoj záznamu informací heslovitě shrnout takto :
-> Papírové děrné štítky a pásky,
kde v určitých přesných pozicích byly v papíru vyražey
malé otvory. Pozice každé dírky nesla jednotku (bit)
informace. Ojediněle se děrné pásky místo papíru
zhotovovaly i z plastové nebo kovové fólie pro menší
opotřebování a větší životnost při opakovaném častém
používání. Počítačové tiskárny (které
tehdy byly často jen upravené elektrické psací stroje) měly někdy nainstalované i děrovače pásků;
informace se tiskla a zároveň děrovala na pásku. Děrné
štítky a pásky se pak vkládaly do elektro-mechanické či
opto-elektronické čtečky kterou procházely,
přečetly z nich zapsaný kód a podle něho vykonaly
požadovanou funkci ve stroji, nebo zadaly počítači data či
funkci jakou má vykonat. Děrné štítky se používaly
především u obráběcích strojů, děrné pásky v
informatice a vědeckém výzkumu, kde bylo velké množství
dat.
-> Magnetická páska, která měla
podstaně větší kapacitu záznamu a dala se zmazat a
následně přepsat novou informací.. Procházela těsně kolem
čtecí či záznamové cívky, která na feromagnetickou vrstvu
pásku elektromagneticky zaznamenala příslušnou magnetizaci. A
při přehrávání (čtení) zmagnetovaná páska při průchodu
kolem čtecí cívky indukovala elektrické napětí, které se
zesilovalo a zpracovávalo. Používala se nejvíce pro
analogový akustický záznam (magnetofonová páska), záznam
obrazu (videomagnetofon) a digitální záznam dat.
-> Magnetický výměnný disk, zvaný
též disketa či floppy disk. Uvnitř
čtvercového plastového obalu byl plochý plastový kotouč
(disk) pokrytý feromagnetickou vrstvou, na niž se pomocí
záznamové cívky ukládaly informace. Data se na rotující
disketu zapisovala v kružnicích a četla se cívkami, které se
po povrchu disku mohly různě posouvat v radiálním směru.
-> Magnetický pevný disk (hard disc)
je nainstalován v počítači pro dlouhodobé uchování
informací, jejich operativní zápis a čtení. Jsou to
především počítačové programy a operační systémy,
nahraná data a soubory. Skládá se z jednoho či několika
kotoučů (disků) na jejichž magnetických vrstvách je v
kruhových stopách zapsána informace (stejně, ale s větší
hustotou, jako na disketě). Kromě pevného vnitřního disku se
někdy používají i další externí disky připojené
konektorem, nyní většinou USB.
-> Optický disk je plochý disk s
lesklým světelně reflexním povrchem, na kterém je
informace uložena pomocí drobných výstupků a prohlubenin,
které jsou zapsány kruhově ve spirále (podobně jako jsou
kružnice u disket a hard disků). Vypalují se většinou
laserem, při větším počtu kopií se někdy mechanicky
vylisují. Jsou čteny laserem, směrovaným na reflexní vrstvu.
Pokud papsek dopadne na vystouplý vrcholek, odrazí se do
čtecího elementu a je převeden na elektrický sigál
"1". Při dopadu do dolíku se neodrazí, čtecí
element nic nezaznamená, což znamená logickou "0".
Byly vyvinuty především dva typy optických disků. CD
(Compact Disc) s kapacitou cca 700 MB a DVD
(Digital Video Disc či Digital Versatile Disc),
který dokáže nahrát až 7-krát větší množství dat než
CD. Na tyto optické disky se nahrává především hudba a
videa, dále počítačové programy a datové soubory.
Speciální miniaturizovanou verzí optického disku je hudební
tzv. MiniDisc (podrobně popsaný v článku "Minidisk.htm").
-> Feritová paměť je tvořena velkým
počtem drobných feritových kroužkových jadérek, které jsou
obtočeny tenkými drátkovými vodiči - miniaturními
"cívečkami" které zapisují a čtou magnetickou
informaci. Každý takový feritový kroužek představije jeden
bit. Není závislá na elektrickém napájení, takže data
zůstávají zachována i po vypnutí počítače.
-> Paměť RAM (Random Acces Memory)
se používá jako operační paměť počítače. Skládá se z
polovodičových elementů, do kterých se pomocí vodivých
materiálů vedou signály, které některé polovodiče
spínají a jiné uzavírají. Sepnuté polovodiče nabíjejí
kondenzátory, což představuje "1", nenabité
"0". Je závislá na stálém elektrickém napájení,
po vypnutí počítače se data anulují; po zapnutí se opět
nahraje operační systém a případná data z pevného disku.
-> "Flash disk" je kompaktní
miniaturizovaná přenosná paměť, která po nahrání není
závislá na elektrickém napájení. Používá se, jakožto
paměťová karta, k přenosu dat mezi počítači a jinými
přístroji. Data se elektricky zapisují do elementárních
tranzistorů uvnitř destičky flash. Každá buňka je tvořena
dvěma tranzistory oddělenýmí vrstvičkou oxidu křemíku.
Pokud je tento oxid vodivý, je buňka ve stavu "1",
pokud je nevodivý ve stavu "0". Vodivost této
vrstvičky se reguluje elektrickým nábojem. Flash disk se k
počítači a jiným digitálním zařízením snadno připojuje
konektorem přes USB (Universal Serial Bus)
interface, který kromě zápisu a čtení dat má též piny pro
elektrické napájení a nabíjení externích zařízení.
Používá se pro připojení počítačové klávesnice a myši,
tiskárny, externích paměťových jednotek, digitálních
fotoaparátů a kamer a dalších.
Pozn.: "Flash
disk" není ve skutečnosti ani "flash"
- blesk (není tam žádný elektrický výboj), ani "disk"
- má tvar malé obdélníkové destičky. Je to jen metaforický
název. Paměťová média v informatice je zvykem nazývat
"disk", i když mají jiný tvar a nerotují. A název
"flash" pramení z toho, že nahrávání a mazání
obsahu je operativní a tím pádem "bleskově rychlé"
ve srovnání s dřívějšími paměťovými technologiemi, kde
byl proces mazání a přepisování dat postupný a relativně
pomalý.
-> Paměť F-RAM (Ferroelectric Access
Memory) je elektricky nezávislá paměť s přímým
přístupem, která dokáže uchovat data i po vypnutí el.
napájení, podobně jako feritová paměť. Buňky paměti F-RAM
využívají zbytkové polarizace feroelektrického materiálu po
vystavení elektrickému poli.
-> Paměť M-RAM (Magnetoresistent
Access Memory) je založený na tzv. ("obří")magnetorezistenci
ve dvou feromagnetických vrstvách, oddělených
nemagnetickou vrstvou (bylo nastíněno výše v pasáži "Magnetický
záznam"). Je ve stadiu vývoje,
zatím nemůže konkurovat F-RAM ...
Spintronika
Klasická elektronika je založena
na elektrickém náboji elektronů a na jejich
pohybu - elektrickém proudu a jím buzeného magnetického
pole. Kromě tohoto náboje však elektrony mají svůj
vlastní rotační moment hybnosti - spin a s
ním spojený magnetický moment. V magnetickém poli (generovaném
třebas cívkou) se elelektrony pohybují, kromě působení
základní Lorentzovy síly, po zlehka odlišných trajektoriích
podle orientace spinu. U volných elektronů je to poměrně
subtilní efekt, detekovaný pouze v některých částicových
experimentech.
V 80.letech 20.stol. se však začal vyvíjet nový obor
spinová elektronika či zkráceně spintronika,
která kromě základního náboje elektronů využívá i jejich
spinovou orientaci a vazbu spin-náboj
pro různá elektromagnetická chování lítek, především
feromagnetických a polovodičových elementů. V praxi se
výrazně uplatňuje ve vícenásobných feromagnetických a
nemagnetických vrstvách, buzených vnějším
elektromagnetickým signálem, jako rozdílná magnetorezistence
v závislosti na orientaci spinů elektronů (GMR senzory byly zmíněny v předchozím odstavci o magnetickém
záznamu).
Přírodní magnety
Již od dob antiky známé magnetické silové působení
nerostů - permanentních magnetů -
bylo dlouhou dobu v chápání přírodovědy oddělené od jevů
elektrických. Nynější teorie magnetických momentů atomů a
molekul ukazuje, že i v permanentních a přírodních magnetech
spočívá původ magnetického pole v interakcích
pohybujících se nábojů. Jedná se o tzv. magneticky
tvrdé feromagnetické látky (většinou obsahující
železo), které si určitou remanentní magnetizaci
zachovávají i bez vnějšího magnetického pole. I zemské
jádro (a jádra některých dalších planet a plasmatické
nitra hvězd) vytvářejí přírodní magnetické pole - viz
"...." .....
Elektromagnetické vlny v
látkovém prostředí
Šíření elektromagnetických
vln v látkovém prostředí je na klasické úrovni dáno Maxwellovými
rovnicemi ( §1.5 "Elektromagnetické
pole. Maxwellovy rovnice"
knihy "Gravitace, černé díry a fyzika
prostoročasu".), v nichž místo vakuových hodnot elektrické
permitivity eo a magnetické
permeability mo vystupují
příslušné koeficienty e a m pro danou látku (jejich původ
byl diskutován výše v pasážích "Elektrické
a magnetické jevy v látkovém prostředí"). Pokud látkové prostředí obsahuje volné nosiče
náboje, bude na pravé straně Maxwellových rovnic vystupovat
nenulová proudová hustota j, která je v
nejjednodušším (lineárním) případě dána Ohmovým
zákonem - ten vyjadřuje přímou úměru mezi specifickou vodivostí
materiálu s a hustotou proudu j, který
materiálem poteče po přiložení elektrického pole E:
j = s.E. Pomocí ohmického měrného
odporu rohm= 1/s se hustota proudu
dá ekvivalentně vyjádřit jako: j = E/rohm .
Tyto Maxwellovy rovnice v látkovém prostředí
mají vlnové řešení
¶2E/¶x2 + ¶2E/¶y2
+ ¶2E/¶z2
= e.m .¶2E/¶t2 + s.m .¶E/¶t ,
které se od běžné vakuové vlnové rovnice liší tím, že
má navíc člen s první derivací podle času s.m .¶E/¶t, který popisuje
ztráty - tlumení - absorpci vlnění v daném
materiálu v důsledku buzení proudů (nazývá
se někdy "telegrafní rovnice",
neboť analogickým způsobem se chová útlum signálu v
telegrafním vedení). Takto vznikající
útlum způsobuje, že pokud do látky dopadá elektromagnetická
vlna kruhové frekvence w=2pf o vstupní intenzitě I0, s rostoucí hloubkou d se bude její intenzita I
snižovat podle exponenciálního zákona
I(d) = I0 . e-[Ö(w.s.m/2)].d
s absopčním koeficientem Ö(w.s.m/2), rostoucím s
frekvencí vlny a měrnou vodivostí materiálu. Někdy se
zavádí hodnota efektivní hloubky průniku
elektromagnetické vlny do látky de = Ö(2/w.s.m) = Ö(rohm/p.f.m), při níž
amplituda elektromag. vlny poklesne na 1/e. Dobrými dielektriky
s nepatrnou vodivostí (s®0, rohm®Ą) procházejí elektromagnetické vlny téměř bez
útlumu do velkých hloubek. Naopak do kovů s velmi dobrou
vodivostí pro volné elektrony (s®Ą, rohm®0) elektromagnetické vlny téměř neproniknou *) , odrážejí se od jejich povrchu
(v elektronice se to projevuje z druhé
strany jako tzv. "skin efekt" u vodičů
jimiž protéká vysokofrekvenční střídavý proud - protéká
pouze při povrchu vodičů). Prostor
odklopený dostatečně hustou drátěnou sítí proto funguje
jako tzv. Faradayova klec, odstíněná proti vnějším
elektromag. vlnám.
*) Např. pro měď s vodivostí s =5,8x107 S/m, neboli měrným elektrickým odporem rohm= 1,68x10-8 W.m
, proniká elektromagnetická vlna frekvence 1MHz do hloubky cca
65 mikrometrů, při frekvenci 300MHz činí hloubka průniku de
jen 3,8 mikrometru.
Faradayova
klec
Na skutečnosti, že v elektricky vodivém předmětu se
elektrické náboje shromáždí na jeho povrchu a dovnitř
neproniknou, je založena tzv. Faradayova klec
či stínící štít *). Máme-li pracovní prostor ze
všech stran obklopený vodivým materiálem - je to dutina
ve vodivém předmětu - okolní elektrické pole způsobí, že
volně pohyblivé elektrické náboje ve vodivém obalu se
kontinuálně rozmístí takovým způsobem, že uvnitř dutiny
se zruší účinek pole .
*) Nazývá se po významném
průkopnikpovi elektromagnetismu M.Faradayovi, který první
takovou klec sestavil a pomocí elektroskopu změřil, že náboj
přivedený na vnější stěnu nezpůsobuje žádné elektrické
pole uvnitř.
Skutečná téměř
dokonalá Faradayova klec je tvořena souvislým obalem z dobře
vodivého materiálu (např. z měděného plechu), bez otvorů a
mezer, kolem vnitřního prostoru. V praxi se však většinou
používají drátěné mřížky či sítě z takových
materiálů. Faradayova klec odstíní vnitřek od elektrického
pole. Nemůže eliminovat stabilní nebo pomalu proměnné
magnetické pole, ale pouze vysokofrekvenční (f~300MHz/d, kde d je velikost klece v metrech). Pro permanentní magnetické pole není kovová
nádoba z dia- nebo paramagnetického materiálu překážkou,
pro střídavé magnetické pole jen částečně v důsledku
elektromagnetické indukce. Feromagnetický kov s vysokou
permeabilitou dokáže částečně odstínit permanentní
magnetické pole tím, že „odkloní“ jeho siločáry kolem
vyšetřovaného prostoru.
Do
značné míry může Faradayova klec odstínit vnitřek i od
elektromagnetických vln. Pro účinné odstínění je nutné,
aby případné mezery, otvory, "oka" v síti byly
podstaně menší než je vlnová délka signálu který
potřebujeme odstínit. Např. vnitřek automobilu je značně
nedokonalá Faradayova klec, která zhorší nebo znemožní
poslech rádia na dlouhých a středních vlnách (bez vnější antény), ale
mobilní telefony tam fungují uspokolivě (k
odstínění nejčastěji používané frekvence 900MHz by okna v
autě musela být velká jen cca 15-20 cm).
Jako účinná Faradayova klec fungují koaxiální kabely
používané v elektronice.
U
elektromagnetické vlny se elektrická a magnetická složka ve
Faradayově kleci chovají poněkud odlišně. Elektrická
složka je ve vodiči vlivem elektrické indukce eliminovaná,
zatímco magnetická složka může lokálně na chvilku proniknout
do určité hloubky stěny a elektromagnetická indukce ji
nemusí stačit okamžitě anulovat. Mohou tím vznikat některé
anomálie poněkud menší stínící účinnosti..?..
Složitější situace je s odstíněním velmi
krátkovlnného - fotonového - záření X a gama. Pro toto
záření i v souvislém obalu Faradayovy klece již samotné
mezery mezi atomy vytvářejí "oka", kterými
vlny~fotony mohou procházet. Zde stínící schopnost nezávisí
na elektrické vodivosti obalových stěn, nýbrž na elektronové
hustotě obalových elektronů atomů materiálu se kterého
je obal vytvořen - na hustotě a pronovém čísle
materiálu. Měděný plech by zde již nebyl optimální,
tvrdší záření gama by jím mohlo snadno procházet. Lepší
by zde byl plech z olova nebo uranu (238U). Nemusel by ani být elektricky vodivý, mohl by to
být třebas barytový beton nebo olovnaté sklo.
Je stručně diskutováno níže
(podrobněji pak v §1.6, pasáž "Absorbce záření v látkách") :
Velmi krátkovlnné
elektromagnetické záření
Tyto obvyklé zákonitosti, plynoucí z klasické elektrodynamiky
kontinua, platí dostatečně přesně pro
"běžné" elektromag. vlny delších vlnových délek (mnohem větší než meziatomární vzdálenosti) a ne příliš vysokých frekvencí (max. do "optických" frekvencí cca 1014Hz, v ojedinělých
případech u některých opticky průzračných dielektrik až
do 1015Hz). Pro hodně vysoké frekvence a krátké vlnové délky
"nestíhají" atomy tak rychle reagovat, odezva látky
již není synchronní. Rozkmitávají se
atomy v krystalové mřížce a v molekulách (kde se mohou excitovat jejich vibrační a rotační
módy), pro vyšší energie se
rozkmitávají i elektrony v atomech (může
docházet k excitacím a ionizacím).
Začínají se uplatňovat kvantové zákonitosti diskrétních
energetických hladin, objevují se elektrony vyzdvižené z
valenčního do vodivostního pásu. Absorpce záření
spočívá ve výměně energie pronikajících fotonů s
prostředím, při níž se část energie přeměňuje na
kinetickou energii atomů látky - teplo.
Průchod či absorpce záření je spektrálně
selektivní, výrazně závisí na vlnové délce
(frekvenci). A pro velmi vysoké frekvence - vysoké
energie fotonů gama a X - již klasické optické
zákonitosti mizí, dochází k diskrétním kvantovým
interakcím (viz §1.6, pasáž
"Interakce záření
gama").
Hloubková závislost absobce záření si zachovává i nadále exponenciální
charakter, avšak absobční koeficienty
již nesouvisejí s elektrodynamikou kontinua (nezávisí na permeabilitě a měrné vodivosti
materiálu), ale jsou dány účinnými
průřezy interakce záření s atomy látky (vycházejí značně složité funkční závislosti
pro různé materiály a energie záření).
Pro elektromagnetické záření X a gama je absorbce
rozebírána v §1.6, pasáž "Absorbce
záření v látkách",
obr.1.6.5.
Opacita
Schopnost látkového prostředí zeslabit záření,
které jím prochází, se nazývá opacita (lat. opacitas = zastínění, stín). Vyjadřuje míru "neprůsvitnosti" látky,
kvantitativně se vyjadřuje podílem intenzity záření
dopadajícího a záření látkou prošlého. Pro delší
vlnové délky je opacita způsobena výše zmíněnými
ohmickými ztrátami, pro krátkovlnné záření je důsledkem
absorpce elektromagnetického záření elektrony v atomech - excitace
a ionizace, či absorpcí a rozptylem volnými
elektrony.
Pozn.: I některá velmi
dobrá dielektrika (schopná tvořit
průzračné krystaly), pokud jsou heterogenní a
multikrystalická, mohou být neprůhledná (opacitní)
v důsledku mnohonásobných lomů, odrazů a rozptylů mezi
jednotlivými krystalky.
Příměsi jiných
("cizích") atomů či molekul v krystalové mřížce
vytvářejí v pravidelné mřížce místní "centra" odlišné
vazbové energie atomů, která se mohou
elektromagnetickou vlnou rozkmitávat do jiných energetických
módů a ovlivňovat tím optické vlastnosti látky. Vede to
většinou ke zvýšené absopci záření určitých vlnových
délek...
Optické vlastnosti látek
Jak bylo shora uvedeno v části "Elektromagnetické
pole a záření", světlo je
elektromagnetické vlnění o krátké vlnové délce (cca
360-750nm). Optické jevy lomu a odrazu světla jsou na
makroskopické úrovni popsány jednoduchými zákony geometrické
optiky. Tyto prosté zákonitosti jsou však na
mikroskopické úrovni důsledkem podstatně komplikovanějších
interakcí elektromagnetického vlnění s atomy a molekulami
látky. Když elektromagnetická vlna prochází materiálem, na
elektrony v atomech a molekulách působí elektrické a
magnetické síly, pod jejichž vlivem se pohybují. Reakcí na
elektrickou složku vlny je kmitavý pohyb
elektronů v materiálu, magnetické pole vyvolává kruhový
pohyb. Tyto pohyby vyvolávají periodickou polarizaci
atomů a molekul látky, což ovlivní vlastnosti vlny a její
šíření. Čím vyšší je efektivní polarizace vyvolaná
vlnou (závisí na koeficientech e,m a na rozdílu
frekvence vlny od vlastní frekvence kmitů atomů a molekul v
látce - bude diskutováno níže), tím pomaleji
se elektromagnetické vlnění šíří v daném optickém
prostředí.
Je třeba si uvědomit, že rozměry atomů látky
jsou podstatně menší (asi o 4 řády) než je vlnová délka
viditelného světla. Taková elekromagnetická vlna proto
"nevidí" jednotlivé atomy a molekuly, ale interaguje
s "kolektivní" odezvou
milionů atomů nebo molekul. Z makroskopického hlediska lze
proto odezvu materiálu na takto "dlouhé"
elektromagnetické vlny popsat dvěma standardními parametry
známými z nauky o elektřině a magnetismu :
- elektrickou permitivitou e, charakterizující
polarizační odezvu na elektrické pole;
- magnetickou permeabilitou m, která vyjadřuje
reakci obíhajících elektronů (tvořících
elementární "proudové smyčky")
na magnetické pole.
Elektromagnetické vlnění pak bude vlnovým
řešení Maxwellových rovnic, v nichž místo
vakuových hodnot elektrické permitivity eo a magnetické permeability mo budou vystupovat příslušné koeficienty e a m pro danou látku ("Elektromagnetické pole a záření"). V dielektrickém
prostředí, průzračném pro elektromagnetické vlny
příslušné vlnové délky, bude rychlost c´=
1/Öem šíření tohoto vlnění
menší než c=1/Öeomo ve vakuu *). Z
Huygensova zákona o vlnění pak plyne, že na rozhraní
dvou optických materiálů s různou rychlostí c1 a c2 šíření vln bude docházet ke změně směru
šíření - k lomu světla podle Snellova
zákona sina/sinb = c1/c2 = n, kde index lomu je
dán právě permitivou a permeabilitou n = Öem. Z téhož Huygensova zákona plyne i zákon
odrazu od prostředí, do jehož nitra nemohou
elektromagnetické vlny proniknout (což jsou především
materiály s volně se pohybujícími elektrony, jako jsou kovy,
příp. některá optická rozhraní).
*) Názorně si toto zpomalení světla
můžeme představit tak, že při průchodu látkou jsou
jednotlivé fotony opakovaně pohlceny atomy či molekulami a
následně opět vyzářeny. Tento mnohonásobný proces absorpce
a reemise způsobuje jejich časové "zdržení", což
se makroskopicky jeví jako zpomalení pohybu. V intervalech mezi
vyzářením jedním atomem a pohlcením sousedním atomem se
však pohybují základní rychlostí c ve vakuu.
Je to však jen pomocná představa,
interakce zde nenastává na úrovni individuálních fotonů s
atomy, nýbrž kolektivně s mnoha tisíci atomy. Ještě
hrubší příměr: Železniční rychlík a osobní vlak, pokud
jsou taženy stejným druhem lokomotivy, se po dráze mezi
nádražími pohybují stejně rychle. Výsledně se však
osobní vlak pohybuje pomaleji vlivem časových zdržení při
mnoha zastávkách.
V látkových optických prostředích je tedy
rychlost světla o něco nižší než ve vakuu a poněkud
závisí na vlnové délce, tj. frekvenci světla - tzv. disperze
*). Např. ve vodě rychlost světla pro červené světlo činí
(zaokrouhleně) 226 000 km/s, pro fialové 223 000 km/s; ještě
pomalejší je v krystalech a ve skle. Ze všech přírodních
materiálů má nejvyšší index lomu diamant (n=2,42),
v němž rychlost světla činí jen 123 881 km/s - vede to k
výrazným optickým efektům lomu a odrazu světla v krystalech
diamantu, z čehož pramení jeho estetická obliba jako šperku.
*) Jev disperze
je způsoben frekvenční závislostí polarizace
dielektrik v proměnném elektromagnetickém poli
procházející vlny. Nabité částice (záporné elektrony a
kladná jádra), které jsou součástí atomů a molekul, jsou
drženy v okolí svých rovnovážných poloh pružnými
(kvasielastickými) elektrickými silami. V poli těchto sil má
každý atom či molekula určitou vlastní frekvenci kmitání fo. Vlivem
dopadajícího elektromagnetického vlnění vykonávají nabité
částice v molekulách a atomech vynucené kmity s frekvencí
rovnou frekvenci dopadajícího vlnění f. Pokud je tato
frekvence daleko od frekvencí fo vlastních kmitů atomů nebo molekul, je výsledná
efektivní polarizace malá a světlo prochází prostředím s
rychlostí jen málo sníženou; zároveň je malá i absopce a
disperze. Jsou-li tyto frekvence blízké, dochází k
částečné rezonanci a rychlost světla se značně liší od
vakuové hodnoty c, neboli index lomu se výrazně liší
od jedné. Pro f<fo index lomu s frekvencí poroste a v okolí fo bude značně
vysoký, pro f>fo se index lomu bude s frekvencí snižovat
("anomální" disperze). Pro frekvence f
blízké fo
se projevuje značná rezonanční absorbce, materiál
je pro světlo této vlnové délky téměř neprůhledný. V
oblasti viditelného světla vykazuje většina materiálů
"normální" disperzi, při níž se inex lomu
s frekvencí zvyšuje. Pro jiné vlnové délky (za oblastí
rezonanční frekvence) se můžeme setkat i s anomální
disperzí.
Při zkracování
vlnové délky elektromagnetického vlnění, tj. s
růstem energie fotonů, začíná již individuální
interakce s jednotlivými atomy a molekulami
látky - postupně mizí zákonitosti geometrické optiky.
Pro oblast měkčího X-záření se uplatňují efekty difrakce
na krystalové mřížce látky, pro tvrdší záření X
a záření g se již žádné optické jevy odrazu a lomu neprojevují,
toto ionizující záření tvrdě interaguje s
jednotlivými atomy prostřednictvím fotoefektu,
Comptonova rozptylu či tvorby elektron-pozitronových párů (viz §1.6 "Ionizující
záření", pasáž "Interakce záření gama", obr.1.6.3).
Elektro-mechanické,
elektro-termické, elektro-chemické, elektro-optické jevy
Vzájemné elektromagnetické interakce atomů a molekul a jejich
interakce s vnějším elektrickým a magnetickým polem jsou
příčinou i řady dalších souvisejících jevů na pomezí
elektřiny a mechaniky, termiky, chemie, optiky, biofyziky.
Můžeme vyjmenovat např. :
¨
Piezoelektrický jev - mechanické deformace některých
krystalů (např. křemene) způsobují vznik opačných nábojů
na stěnách těchto krystalů. A naopak, přiložíme-li k
protilehlým stěnám krystalu elektrody s opačnými náboji,
krystal se v tomto směru nepatrně zdeformuje (elektrostrikce).
Obdobný elektrický účinek nastává i při ohřívání
krystalů - pyroelektrický jev.
¨
Magnetostrikce - změna délkových rozměrů a objemu
způsobená zmagnetováním feromagnrtických látek.
¨
Termoelektrický jev - vznik elektrického napětí či
proudu při zahřátí materiálů na různou teplotu. A naopak
vznik tepelných gradientů při průchodu elektrického proudu.
Příčinou těchto jevů je tepelný pohyb a difúze volných
nositelů elektrického náboje. Patří sem Thomsonův jev
ve vodiči, na němž je teplotní gradient, nebo Seebeckův
a Peltierův jev na rozhraní dvou vodičů s různou
Fermiho hladinou, kdy vzniká kontaktní potenciál.
¨
Fotoelektrický jev - emise elektronů či změna
elektrických vlastností látky při ozařování světlem. Při
dopadu elektromagnetického vlnění na látku dochází k
interakci s atomy a s elektrony ve valenčním nebo vodivostním
pásu. Při absorbci této energie slabě vázaným elektronem ve
vodivostním pásu může dojít k jeho fotoemisi - vnější
fotoelektrický jev. Pokud je zářivá energie absorbovaná
elektronem ve valenční pásu, může dojít k jeho přeskoku do
vodivostního pásu - vnitřní fotoelektrický jev,
čímž vzniknou volné nosiče elektrického náboje a nastane
(či vzroste) vodivost materiálu.
¨
Elektroluminiscence - vyzařování fotonů světla
účinkem průchodu elektrického proudu. Fotony světla
vznikají při přeskoku elektronů z vyšší energetické
hladiny vodivostního pásu do nižší hladiny valenčního
pásu (dochází k rekombinaci elektronu s dírou), popř. přes
hladinu vhodné příměsi. V tzv. LED diodách k tomuto jevu
dochází v oblasti přechodu p-n.
¨
Elektrochemické jevy - změna chemického složení
sloučenin a chemické reakce vyvolané průchodem elektrického
proudu. Je to především elektrolýza - vylučování
látek na elektrodách při průchodu elektrického proudu
roztokem disociovaných sloučenin (elektrolytem).
¨
Elektrické výboje v plynech - průchod elektrického
proudu ionizovaným plynem. Ke vzniku volných nosičů
elektrického náboje - elektronů a iontů, neboli k ionizaci,
dochází buď zahřátím na vysokou teplotu, nebo absorcí
elektromagnetického či korpuskulárního záření dostatečné
energie kvant. Ionizaci mohou způsobovat a udržovat i elektrony
a ionty urychlené elektrickým polem mezi elektrodami při
vlastním výboji.
Plasma - 4.skupenství látky
Za vysokých teplot, v elektrickém výboji či působením
ionizujícího záření, jsou z atomů plynu vyráženy
elektrony a samotné atomy se stávají kladnými ionty.
Takovýto částečně nebo plně ionizovaný plyn
se nazývá plasma (řec. plasma
= tvárný materiál; elektrický výboj kopíruje tvar
trubice a jeho tvar je snadno ovlivnitelný elektrickým a
magnetickým polem). Plasma se někdy
označuje za 4.skupenství hmoty (1.pevná
látka, 2.kapalina, 3.plyn, 4.plasma). Abychom odlišili tuto
ionizovanou látku od jiných situací s elektricky nabitými
částicemi, ve fyzikální definici plasmy požadujeme dvě
další vlastnosti :
- Elektrickou neutralitu v
makroskopickém měřítku (v průměru stejný počet elektronů
a kladných iontů) - nepovažujeme tedy za plasmu svazky
nabitých částic;
- Kolektivní chování způsobené
dlouhodosahovou interakcí dostatečně blízkých nabitých
částic - není tedy plasmou velmi zředěný či slabě
ionizovaný plyn.
Obecná fyzikální definice plasmy tedy zní: "Plasma
je soubor částic s volnými nosiči nábojů, který je
globálně neutrální a vykazuje kolektivní chování".
Tato definice zahrnuje i exotické formy látky, jako je kvark-gluonová
plasma (§1.5, pasáž "kvark-gluonová plasma - "5.skupenství
hmoty"").
Plasma vykazuje výrazné elektrické vlastnosti:
je elektricky vodivá, reaguje na magnetické pole, sama může
generovat elektrické a magnetické pole, probíhají v ní
složité elektro- a magneto-dynamické procesy. Právě tyto
jevy jsou velmi důležité v astrofyzikálních dějích v
horkých ionizovaných plynech ve vesmíru.
V běžné pozemské přírodě se plasma vyskytuje jen
poměrně zřídka v atmosférických výbojích, blescích. Z
globálního hlediska je však plasma velmi důležitá
forma hmoty - většina pozorované látky ve vesmíru
je v plasmatickém skupenství. Plasma má velký význam pro
dosažení termonukleární fúze - §1.3, část "Slučování atomových jader".
Atomové
jádro
Nahlédněme nyní hluboko do
nitra atomu - přímo do samotného atomového jádra.
Než se budeme zabývat stavbou atomového jádra, stojí za
povšimnutí jeho velikost v porovnání s
velikostí atomu. "Průměr" atomu je řádově »10-8 cm (je tedy hluboko
pod rozlišovací schopností optického mikroskopu - atom je
mnohem menší než vlnová délka světla; ani elektronovým
mikroskopem nejsou atomy přímo pozorovatelné). Jádro je však
ještě 100 000 - krát menší! - jeho "průměr"
činí jen »10-13cm. Přitom je v jádře soustředěna
téměř veškerá hmotnost (více než 99,9%) atomu. Hustota, s
jakou je hmota "namačkána" v atomovém jádře, je
tedy nepředstavitelně vysoká - r »1014g/cm3!
Představit si tak obrovskou hustotu není
snadné: kdyby např. krabička od zápalek byla naplněna
jadernou hmotou, vážila by asi miliardu tun (!) - prorazila by
stůl, půdu i horninu a propadla by se do středu Země. Kromě
atomových jader se nikde v okolní přírodě s tak vysokou
hustotou nesetkáváme. Avšak ve vesmíru byla objevena
podivuhodná tělesa zvaná neutronové hvězdy.
Jsou to hvězdy na konci svého života s vyčerpaným jaderným
"palivem", gravitačně zhroucené do rozměrů pouze
desítek kilometrů, jsou složeny z neutronů s hustotou právě
»1014g/cm3. Rychle rotují a
při interakci nabitých částic se silným magnetickým polem
vzniká elektromagnetické záření, které při rotaci hvězdy
"zametá" okolní prostor podobně jako světlo
rotujícího majáku - pozorujeme je jako pulsary.
Podrobnosti můžeme nalézt v kap.4 "Černé díry" knihy "Gravitace, černé díry a fyzika
prostoročasu".
Ze samotného faktu tak malých
rozměrů a fantastických hustot v atomovém jádře plyne - a
to i bez znalosti konkrétní struktury jádra, že v atomových
jádrech budou působit veliké síly a budou
zde "ve hře" vysoké energie (tím se
budeme zabývat v §1.3, část "").
Poznámka: Z
těchto skutečností je zároveň naprosto jasné, že alchymisté
snažící se uskutečnit transmutaci prvků (např. olovo
přeměnit ve zlato) neměli nejmenší naději na úspěch!
Metodami, které měli k dispozici (mletí, roztloukání,
žíhání, hoření, chemické slučování) pouze
"škrábali" atomy po jejich nejsvrchnějších
(valenčních) slupkách. Pokud by chtěli změnit prvek, museli
by proniknout stotisíckrát hlouběji do nitra atomu, změnit
jádro a tím teprve by dosáhli transmutace. K tomu samozřejmě
neměli prostředky, energii ani znalosti. Nyní to jaderná
fyzika již v zásadě umí, a to metodami
"ostřelování" jader elementárními částicemi
urychlenými na vysoké energie (takto se však dá připravit
jen mizivě malém množství transmutovaných prvků).
Struktura atomového
jádra
Existenci kladně nabitého, velmi
malého a hutného atomového jádra přesvědčivě dokazovaly
shora zmíněné rozptylové experimenty E.Rutheforda a spol. z
r.1911 (obr.1.1.4),
avšak o vlastní povaze a stavbě atomového jádra se z těchto
experimentů nedalo nic usuzovat. Podobný klíčový význam,
jaký měl pro odhalení stavby atomů objev elektronu, sehrál
pro vyjasnění stavby atomových jader objev protonu,
kladně nabité těžké částice, učiněný rovněž
Ruthefordem při sledování stop částic a ve Wilsonově mlžné
komoře.
Při nárazu částic a na jádra dusíku docházelo k reakci 4a2 + 14N7 ® 17O8
+ 1p1. Z místa srážky
vycházely dvě stopy, z nichž jedna odpovídala jádru
kyslíku, druhá pak kladné částici totožné s jádrem
vodíku - tato částice byla nazvána proton.
Proton jako elementární částice se značí "p",
nebo alternativně, podle chemické terminologie, "H"
či 1H1 jakožto jádro
vodíku. Skutečnost jeho kladného elementárného náboje se
někdy vyznačuje indexem "+", tj. p+. Dalšími měřeními byly postupně stanoveny
vlastnosti a fyzikální charakteristiky protonu, viz §1.5
"Elementární částice".
Okamžitě se nabízela představa, že
jádra atomů jsou složena z protonů.
Podporovala jej i pozoruhodná pravidelnost v hmotnostech atomů
- že hmotnosti všech atomů jsou téměř přesně
celočíselnými násobky hmotnosti atomu vodíku. Model jádra
složeného jen ze samotných protonů však narážel na dva
problémy:
Především to bylo elektrické Coulombovské odpuzování
souhlasně nabitých protonů, které by na tak malých
vzdálenostech bylo nesmírně silné a tehdy nebyly známé
žádné jiné síly, které by mu mohly čelit a udržet stabilitu
jádra. Dále, hmotnosti všech atomů kromě vodíku vycházely
zhruba poloviční, než bylo ve skutečnosti
pozorováno.
Proto byly dočasně navrhovány modely, v nichž se v jádře kombinovaly
protony a elektrony: jádro prvku s atomovým číslem Z
by se skládalo z 2.Z-protonů (tedy dvojnásobku protonů) a
Z-elektronů, jejichž záporný náboj by kompensoval
nadbytečný kladný náboj. Proton-elektronový model dával
přibližně správné hodnoty hmotnosti pro lehká jádra,
nikoli však pro těžká jádra. Radioaktivita b, při níž
dochází k emisi elektronů z jader, zdánlivě podporovala
tento model s "jadernými elektrony". Další
vlastnosti jader však již nebyly s tímto modelem v souladu
(např. magnetický moment jader by vycházel podstatně
vyšší).
Chybějící článek k objasnění stavby atomového jádra
byl doplněn až objevem neutronu, učiněný
J.Chadwickem r.1932 při experimentech s ostřelováním jader
berylia částicemi a. Ukázalo se, že tyto neutrony, částice zhruba
stejně těžké jako protony ale bez elektrického náboje, jsou
zřejmě onou záhadnou chybějící složkou, která je spolu s
protony v atomových jádrech. Složení jader z protonů a
neutronů zároveň přirozeně vysvětlilo existenci isotopů:
isotopy jednoho prvku obsahují stejný počet protonů (proto
mají stejné chemické chování), ale různý počet neutronů,
takže se liší jen hmotností.
Ve Wilsonově mlžné komoře byla po srážce částice a s jádrem Be
pozorována jen jedna stopa, která náležela jádru uhlíku C.
Když Chadwick provedl podrobnou analýzu stop částic a a C z
hlediska zákonů zachování energie a hybnosti, dospěl k
závěru, že při srážce kromě jádra uhlíku musí vznikat
ještě jedna poměrně těžká a energetická částice, která
nenese elektrický náboj a proto nevytváří ionizační stopu
v mlžné komoře. Dochází tedy k reakci 4a2 + 9Be4 ® 12C6
+ 1n0; nově objevená
neutrální částice (o hmotnosti o maličko větší než
protonu) byla nazvána neutron, označuje se
"n". Elektrická neutralita neutronu se někdy
vyznačuje indexem nula "o", tj. no. Dalšími experimenty byly postupně stanoveny
ostatní vlastnosti a fyzikální charakteristiky neutronu, viz
opět §1.5 "Elementární částice".
Bylo tedy zjištěno, že atomová jádra se
skládají ze dvou druhů těžkých částic (nukleonů): protonů
a neutronů, přičemž tyto protony a neutrony
jsou v jádře drženy novým, do té doby neznámým, typem sil
- tzv. jadernými silami (viz níže).
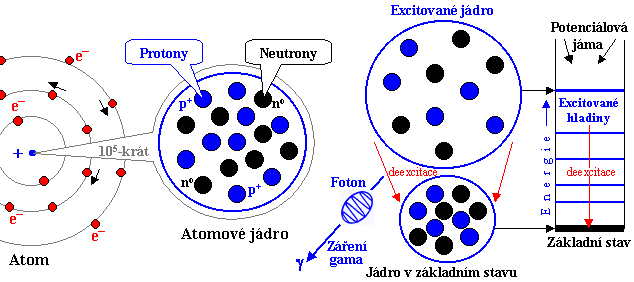 |
| Obr.1.1.9. Schématické znázornění stavby atomového jádra. V pravé části jsou znázorněny energetické hladiny jádra, excitované jádro a jeho deexcitace za emise fotonu záření gama. |
Na obr.1.1.9 je atomové jádro pomyslně
"zvětšeno" celkově asi 1014-krát a je zde schématicky znázorněna jeho
struktura. Jádro se skládá z částic dvou druhů souhrnně
nazývaných nukleony: kladně nabité protony
p+ a neutrony no bez elektrického náboje. Počet protonů v jádře,
zvaný protonové číslo Z, jednoznačně
určuje zároveň i konfiguraci elektronů na
jednotlivých slupkách atomového obalu (každé jádro si
"přibere" tolik elektronů, aby bylo elektricky
neutrální) a tím tedy chemickou povahu atomu
- protonové číslo Z je zároveň pořadovým číslem v
Mendělejevově periodické tabulce chemických prvků. Číslo Z
se proto někdy nazývá atomové číslo. Celkový
počet nukleonů, zvaný nukleonové číslo N,
určuje hmotnost atomového jádra v násobcích hmotnosti
protonu či neutronu; nukleonové číslo N se též někdy
nazývá hmotnostní číslo a značí se A.
Jádra se stejným počtem protonů, které mají různý počet
neutronů, se nazývají isotopy - chemické
vlastnosti příslušných atomů jsou stejné, liší se jen
hmotností (viz níže pasáž "Fyzikální
a chemické vlastnosti isotopů"). Jádra značíme písmeny chemického označení podle
Mendělejevovy tabulky prvků (zde obecně označíme X),
přičemž jako horní index připojujeme nukleonové číslo a
jako dolní index číslo protonové: NXZ - např. vodík 1H1,
héluim 4He2, uhlík 12C6, uran 238U92. Vzhledem k tomu,
že protonové číslo je jednoznačně určeno názvem prvku v
Mendělejevově tabulce, dolní index se často vypouští
(např. místo 12C6
se zkráceně píše jen 12C).
Velikosti (průměry) atomových
jader (z hlediska silné interakce) se pohybují v rozmezí od cca 1,6 fm (tj. 1,6.10-13cm) pro atom vodíku - průměr 1 protonu, do cca 15
fm (tj. 1,5.10-12cm) pro nejtěžší atomy z
oblasti uranu a blízkých transuranů (o
velikosti částic v mikrosvětě viz též §1.5, pasáž "Velikost,
rozměry a tvar částic?").
Fyzikální a
chemické vlastnosti isotopů
Různý počet neutronů v jádrech isotopů má přirozeně vliv
na jejich fyzikální a částečně, v daleko menší míře, i
na chemické vlastnosti. Fyzikální vlastnosti
isotopů můžeme rozdělit na jaderné a atomové.
Odlišné jaderné vlastnosti různých isotopů
téhož prvku spočívají ve třech aspektech :
-
Různé průběhy (druh, účinný průřez) interakcí a
jaderných reakcí při ostřelování jader různých
isotopů částicemi nebo při jejich vzájemných srážkách (to je podrobně rozebíráno v §1.3 "Jaderné reakce a jaderná energie").
- Na
počtu neutronů, vzhledem k počtu protonů, závisí stabilita
či nestabilita - příp. radioaktivita,
jader s různým počtem neutronů (§1.2
"Radioaktivita", zvláště část "Stabilita
a nestabilita jader"). Často stačí jen o jeden neutron v jádře víc nebo
míň a již je příslušný isotop radioaktivní (vlastnosti radioaktivních isotopů jsou podrobně
studovány v §1.4 "Radionuklidy").
-
Dále jsou to různé hodnoty magnetického momentu
jader, podle počtu spárovaných a nespárovaných protonů a
neutronů - může být důležité v analytické metodě nukleární
magnetická rezonance (viz §3.4,
část "Nukleární magnetická rezonance").
Poněkud
odlišné atomové vlastnosti různých isotopů
jsou způsobeny rozdíly v hmotnostech atomů,
daných různým počtem neutronů v jádrech téhož prvku.
Výrazněji se to projevuje především u lehkých prvků s
nízkým protonovým číslem. Atom vodíku 2H1 - deuteria D,
je 2-krát těžší než atom obyčejného vodíku 1H1. A jeho sloučenina
s kyslíkem, "těžká voda" D2O,
má asi o 10% vyšší hustotu než obyčejná "lehká"
voda H2O. Teplota tuhnutí těžké vody je (místo 0°C u obyčejné vody)
3,8°C, teplota varu 101,4°C.
Chemické vlastnosti atomů -
způsoby jejich vazby a reakcí s jinými atomy - jsou dány
konfigurací elektronů v atomových obalech, což závisí na
počtu protonů v jádře, nikoli na počtu neutronů. Různé
isotopy téhož prvku mají tedy stejné chemické
vlastnosti. To je velmi důležité v jaderné chemii a
v aplikacích radionuklidů v laboratorních metodách (§3.5 "Radioisotopové
stopovací metody"), biologii a medicíně (zvláště
v nukleární medicíně - kap.4 "Radioisotopová scintigrafie"). Jediné, v čem se může
chemie různých isotopů stejného prvku poněkud lišit,
je rychlost chemických reakcí. Větší počet
neutronů v jádře znamená, že atomy takového vyššího
isotopu jsou těžší a tím jsou v reakční
směsi o něco pomaleji pohyblivé než lehčí
isotopy. Chemické reakce s těžšími isotopy budou proto za
jinak stejných podmínek probíhat poněkud pomaleji
- kinetický isotopový efekt. Nejvýrazněji se to
projevuje u deuteria, kde to dokonce vede k biologické
toxicitě tohoto isotopu jinak biogenního vodíku.
Nahrazení běžného vodíku jeho těžším isotopem deuteriem
výrazně zpomaluje rychlost biochemických reakcí -
působí jako "brzda" na řadu životních procesů v
buňkách. To má negativní účinky zejména u vyšších
organismů, kde vyšší obsah deuteria (nad
cca 30%) může způsobit smrt.
Silné
jaderné interakce
Podíváme-li se na tento model jádra z hlediska zákonitostí
elektřiny, hned vyvstává zásadní námitka či otázka: Jak
je možné, že jádro drží pohromadě?
Stejnojmenně nabité protony se podle Coulombova zákona budou
odpuzovat, takže by se okamžitě "rozprskly" do
okolního prostoru, žádná jádra a atomy (kromě vodíku) by
nemohly existovat. Ve skutečnosti se však (naštěstí) nic
takového neděje, jádra nám většinou drží hezky
"pohromadě". Kromě elektrických odpudivých sil zde
proto musí působit ještě jiné síly, které jsou
přitažlivé a jsou silnější než elektrické - tyto síly
pak překonávají elektrické odpudivé síly a udržují jádro
pohromadě. Nazývají se silné jaderné interakce;
jejich podstata bude stručně diskutována níže. Jsou asi
100-krát silnější než síly elektrické, ale vykazují jednu
specifickou zvláštnost - mají krátký dosah.
Působí efektivně jen do vzdálenosti r »10-13cm, zatímco pro větší vzdálenosti jsou již
zanedbatelně slabé - se vzdáleností r rychle
exponenciálně klesají. Potenciál těchto sil se často
modeluje tzv. Yukawovým potenciálem
U(r) = g . e-d .
r / r ,
kde g je konstanta vyjadřující sílu interakce a parametr d =
1,6.10-13cm charakterizuje dosah
jaderných sil.
Pozn.: Charakteristická
délka 10-13cm, důležitá v jaderné fyzice, se někdy nazývá 1
Fermi; je to zároveň 1 femtometr [fm].
Každý nukleon může
interagovat bezprostředně pouze s určitým omezeným počtem
sousedních nukleonů - jaderné síly vykazují nasycení.
To je hlavním důvodem snížené stability těžkých jader,
jak bude níže ukázáno (§1.2, §1.3). Jelikož
elektrostatické (Coulombovské) odpuzování protonů je
dlouhého dosahu a působí znatelně v celé oblasti jádra, je
určitá hranice schopnosti silné interakce mezi nukleony
zabraňovat rozpadu velkých jader. Na této hranici je jádro
vizmutu 209Bi83, které je nejtěžším stabilním jádrem *);
všechna těžší jádra se Z>83 a N>209 se již
samovolně přeměňují na lehčí jádra (především
radioaktivita a) - viz §1.2 "Radioaktivita".
*) Donedávna byl bismut-209 skutečně považován za
nejtěžší stabilní nuklid. V r.2003 byla však v jaderných
laboratořích v Orsay prokázána jeho slabá radioaktivní
přeměna alfa-rozpadem s velmi dlouhým poločasem 2.1019let na 205Tl. Při tak
dlouhém poločasu je radioaktivní přeměna prakticky
nepozorovatelná a isotop 209Bi se jeví jako stabilní. Za nejtěžší skutečně
stabilní isotop je nyní považováno olovo 209Pb.
Jaderné síly nezávisí na
typu nukleonů, jsou nábojově nezávislé.
Silné jaderné interakce tedy působí jak mezi protony a
protony, tak mezi protony a neutrony či mezi neutrony navzájem
- protony a neutrony patří do skupiny částic zvané hadrony
(viz níže §1.5 o elementárních
částicích). Detailnější rozbor
ukázal, že jaderné síly jsou spinově závislé
(interakce mezi nukleony závisí na
úhlu mezi spinem a spojnicí obou částic) -
interakce mezi dvěma nukleony s paralelními spiny se poněkud
liší od interakce nukleonů s antiparalelními spiny.
Vliv slabých
interakcí na stavbu jader
Kdyby v mikrosvětě existovala jen silná
interakce (a elektromagnetická), mohly by existovat i "mononukleonová"
jádra složená jen z protonů nebo jen z neutronů (mononeutronová jádra by neměla elektronový obal). Mohly by vznikat i jaderná "monstra"
složená i z tisíců neutronů. Nic takového však v
přírodě nepozorujeme, neexistují stabilní jádra ani ze dvou
samotných protonů nebo ze dvou neutronů; i samotný neutron je
nestabilní. V přírodě totiž působí další druh sil - slabá
interakce, která radioaktivitou beta (- nebo
+) nemilosrdně přemění každé jádro, u
něhož je porušen určitý poměr mezi počtem protonů a
neutronů. Mechanismy těchto procesů jsou rozebírány v §1.2,
část "Radioaktivita
beta".
Podstata silných
interakcí mezi nukleony
Podle starší koncepce, kterou v r.1935 navrhl H.Yukawa, jsou
jaderné síly způsobeny výměnou p-mezonů
mezi nukleony. Tato představa se sice zdála poměrně dobře
vysvětlovat některé tehdy známé vlastnosti jaderných sil,
avšak při dalších výzkumech se ukázalo, že skutečnou
příčinu jaderných sil (a silných
interakcí mezi hadrony obecně) je třeba
hledat na hlubší úrovni - ve vnitřní struktuře
protonů, neutronů, p-mezonů a dalších hadronů. Podle dnešní koncepce
primární příčinou "silných interakcí" mezi
hadrony jsou gluony zprostředkované
silné interakce mezi kvarky uvnitř hadronů.
Pozorované "silné" interakce mezi hadrony, a tedy i
jaderné síly, jsou jakýmsi "zbytkovým projevem"
těchto primárních interakcí mezi kvarky. Zjednodušeně si to
můžeme představit tak, že gluony částečně "prosakují"
zevnitř do blízkého okolí protonů či neutronů a
způsobují tam přitažlivé jaderné síly.
Je pozoruhodné, že u vlastních silných interakcí mezi kvarky
se předpokládá dlouhý dosah, přičemž
pozorovaný krátký dosah výsledných interakcí mezi hadrony
(a tedy i jaderných sil) je důsledkem mechanismu
"zbytkového projevu" těchto sil
(další diskuse viz §1.5 "Elementární částice",
část "Interakce elementárních částic", "Kvarková struktura hadronů" a "Čtyři
typy interakcí ").
Pozn.: Je
zajímavé, že s podobným mechanismem se setkáváme i u
interakcí a chemického slučování atomů:
krátkodosahové "chemické" síly mezi atomy jsou zbytkovým
projevem dlouhodosahových elektrických sil od protonů
v jádře a elektronů v obalu, které se vektorově sčítají:
ve větších vzdálenostech se ruší, v krátkých
vzdálenostech zůstává nenulový "zbytek" - viz
výše "Interakce atomů".
V běžně užívaném názvu "silné jaderné
interakce" je slovo "jaderné" vsunuto proto, že
se většinou zabýváme vlastnostmi atomového jádra, v nichž
se tyto interakce uplatňují nejpodstatněji. V částicové
fyzice stačí jen název "silné interakce",
neboť toto jsou fundamentální síly působící obecně mezi interagujícími
hadrony - jako zmíněný důsledek silné interakce
mezi kvarky tvořícími hadrony. Jaderné síly jsou jen
speciálním projevem těchto silných interakcí.
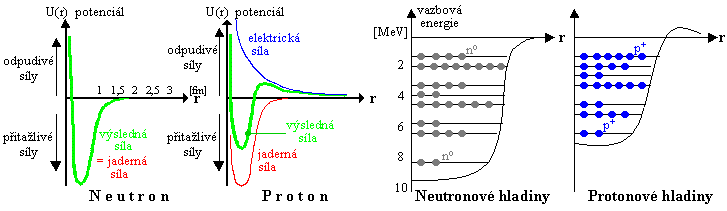
Obr.1.1.10. Grafické znázornění
potenciálů jaderných sil pro neutron a proton v závislosti na
vzdálenosti. V pravé části obrázku jsou znázorněny
diskrétní (kvantové) energetické hladiny nukleonů v
potenciálové jámě jádra.
Na obr.1.1.10 je graficky znázorněno, jak
potenciály sil působících mezi jádrem a nukleonem závisejí
na vzdálenosti. Představme si v myšleném pokuse, že nukleon
pomalu přibližujeme k atomovému jádru. Pro neutron no (vlevo) bez
elektrického náboje působí pouze pole silné interakce,
takže ve větších vzdálenostech je síla zanedbatelná a ve
vzdálenostech řádově 10-13cm působí přitažlivá síla, která
sváže neutron s jádrem. Pro kladně nabitý proton p+ bude ve větších
vzdálenostech působit elektrická odpudivá síla
podle Coulombova zákona (modrá křivka na obr.1.1.10), a teprve
když ji překonáme (říkáme, že jsme
překonali Coulombovskou bariéru) a proton
se přiblíží k jádru na vzdálenost blízkou 10-13cm (1 fm), začne
působit přitažlivá jaderná síla (červená
křivka), která překoná elektrickou odpudivou sílu a
"přiváže" proton k jádru. Křivka potenciálu
výsledné síly je v obou případech na obrázku vyznačena
zeleně. V ještě menších vzdálenostech (desetiny fm) uvnitř
jádra je pak přitažlivá síla v obou případech efektivně
vystřídána odpudivou silou *), zabraňující
úplnému smrštění jádra; její původ souvisí s kvantovým
principem neurčitosti a s vylučovacím principem fermionů.
*) Jaderné
interakce na subnukleárních vzdálenostech
Na krátkých vzdálenostech řádově desetiny fm mají jaderné
interakce odpudivý charakter. Toto
"odpuzování" nukleonů při jejich vzájemném
přiblížení na vzdálenost <<1 fm není nějakou
specifickou vlastností jaderné silné interakce (která je
zbytkovým projevem silné interakce mezi kvarky uvnitř
nukleonů), či "nestlačitelnosti" nukleonů, ale je
jen "efektivní silou", která je důsledkem kvantových
relací neurčitosti a fermionového charakteru
nukleonů (Pauliho vylučovací princip). Menší vzdálenost,
neboli nižší energetickou hladinu v poli jaderných sil než
je ta nejnižší základní, nemohou nukleony nabývat;
kdybychom se je pokusili "natlačit" ještě blíže k
sobě, "bránily" by se intenzívní odpudivou silou -
nukleony jako by se svou vlnovou povahou "nevešly" do
tak malého prostoru.
Tento efekt vede k tzv. Fermiho tlaku degenerovaného
fermionového plynu v konečných stádiích evoluce hvězd,
který může zastavit gravitační kolaps a vyvážit mohutné
gravitační síly (§4.2 "Konečné fáze hvězdné
evoluce. Gravitační kolaps"
v monografii "Gravitace, černé díry a fyzika
prostoročasu"). Avšak jen tehdy, pokud hmotnost hvězdy
není příliš velká - v tom případě nastupuje silná
gravitace podle obecné teorie relativity za vzniku horizontu
událostí, která "přemůže" i tento kvantový
protitlak a úplný katastrofální gravitační kolaps
zvítězí a utvoří černou díru.
Průběh interakčního potenciálu nukleonů pro
vzdálenosti desetiny fm je do značné míry spekulativní,
v jádrech se nerealizuje a nelze jej experimentálně ověřit.
Nemůžeme dva protony "vzít do ruky", tlačit je
blízko k sobě a měřit síly, kterými se přihují či
odpuzují. Lze to uskutečnit jen srážkovými
experimenty za vysokých kinetických energií. Při
středních energiích (jednotky až desítky MeV) se v
rozptylových experimentech naměří závislost podle
obr.1.1.10, avšak jen s částí odpudivé složky. Pro větší
interakční "přiblížení" nukleonů je potřeba
použít větší srážkové energie stovky MeV. Zde se však
asi od 300MeV projevuje nový jev: produkce p-mesonů
(pionů). Narážíme zde již na skutečnost, že
krátkodosahové jaderné síly jsou zbytkovým projevem
dlouhodosahové silné interakce mezi kvarky uvnitř
nukleonů, zprostředkovaných gluony. Při snaze o co
nejbližší přiblížení nukleonů již nedostáváme žádný
reálný interakční potenciál, neboť se nám nukleony
"roztaví" do kvark-gluonové plasmy,
přestanou "individuálně" existovat a my pozorujeme
vznik množství sekundárních částic odrážejících
vlastnosti nového stavu hadronové látky (§1.5, "Kvarková
struktura hadronů"). Nukleony
při vyšších energiích nejsou nestlačitelné,
ale mění se na nové stavy a částice.
Experimentální měření
(s rozptylem vysokoenergetických elektronů) ukazují, že pro poloměr
jader platí přibližný vztah R = d . N1/3, kde N je
nukleonové číslo jádra a parametr d má hodnotu d =
1,3x10-13 cm - je to dosah silné interakce.
Z tohoto vztahu plyne, že objem jádra je přímo úměrný
nukleonovému číslu N a tedy každý nukleon zaujímá v
jádře zhruba stejný objem. Jádro lze tedy považovat za
soustavu nukleonů s přibližně konstantní hustotou jaderné
hmoty.
Neutrony bez elektrického náboje vykazují pouze
přitažlivé jaderné síly - pomáhají
"stabilizovat" jádro. Pro každé jádro existuje
určitý poměr počtu protonů a neutronů, pro který je jádro
nejstabilnější (tento poměr je pro lehká jádra blízký
1:1, pro těžká jádra se pohybuje až kolem 1:1,5 ve prospěch
neutronů). Pokud jádru se stabilní konfigurací protonů a
neutronů nějaké neutrony přidáme či odebereme, zpravidla
takové jádro již nebude stabilní, ale bude se samovolně
rozpadat (resp. přeměňovat) - bude radioaktivní
(příslušné mechanismy budou
analyzovány v §1.2 "Radioaktivita").
Spinová
závislost jaderných sil
Shora uvedený Yukawův potenciál a grafy potenciálů a
vazbových energií jaderných sil na obr.4.1.10 ukazují jen
základní vlastnosti silné jaderné interakce mezi nukleony v
jádře. Podrobnější analýza ukázala, že kromě
vzdálenosti závisí jaderná síla mezi nukleony i na orientaci
jejich spinu, resp. na spin-orbitální
interakci mezi nukleony. Pro správné rozložení a
obsazení slupek protony nebo neutrony v potenciálové jámě
jádra bylo třeba zavést přídavný potenciál odpovídající
spin-orbitální vazbě, tj. závislosti
jaderné interakce na vzájemné orientaci spinu a orbitálního
momentu nukleonu. Bylo změřeno, že jaderná přitažlivá
síla mezi dvěma nukleony je silnější pokud mají souhlasně
orientovaný spin a slabší když mají spin opačně
orientovaný. Tento fenomén je způsoben odlišným skládáním
interakcí mezi kvarky ve složitém zbytkovém projevu silné
interakce, vytvářejícím jaderné síly. Detaily těchto
mechanismů zatím nejsou náležitě prozkoumány.
Jedním z důsledků spin-orbitálních interakcí
mezi nukleony je zvýšená stabilita jader s nukleonovým
číslem 2, 8, 20, 8, 50, 82 a 126 - "magická čísla"
( viz níže "Modely atomového jádra",
pasáž "Slupkový model jádra"). A naopak
snížená síla jaderné interakce u částic s opačným
spinem, která je příliš slabá na to, aby je svázala - viz
níže "Různorodost atomových jader",
pasáž "Neexistence diprotonů a dineutronů".
Excitované stavy jádra
Nukleony se v jádře nacházejí a pohybují v poli
jaderných sil (silné interakce), v němž mohou mít
různou (vazbovou) energii - pohybují se v jakési "potenciálové
jámě". Podle zákonitostí kvantové fyziky
přitom nukleony nemohou mít plynule proměnnou energii v tomto
poli, ale jen určité kvantované hodnoty
energie. Tedy podobně jako elektrony v atomovém obalu, i v
jádře se nukleony nacházejí na diskrétních
energetických hladinách (obr.1.1.9 a 1.1.10, oba
vpravo). Protonové a neutronové hladiny se vlivem elektrické
interakce poněkud liší a jsou obsazovány nezávisle,
přičemž Pauliho vylučovací princip omezuje obsazení každé
takové hladiny max. dvěma protony a dvěma neutrony s
opačnými spiny. Nejnižší energetická hladina jádra
odpovídá základnímu stavu, ale jádro se
může (dodáním energie - excitací) dostat i do
vyššího energetického stavu - na tzv. vzbuzené
neboli excitované energetické hladiny - jako
kdyby jádro bylo "nafouknuté", nukleony jsou
"dále od sebe" (obr.1.1.9), obsazují vyšší
hladiny. Takto energeticky vzbuzené jádro zpravidla velmi
rychle "splaskne" - hladiny se deexcitují,
přičemž příslušný rozdíl energií se vyzáří
ve formě fotonu elektromagnetického záření
- záření g (viz §1.2,
část "Záření gama").
Vedle základního stavu mají atomová jádra (kromě vodíku) řadu
excitovaných stavů (energetických hladin), z nichž
jen část se uplatňuje při radioaktivních přeměnách. Ty
ostatní excitované stavy vznikají při ostřelování jader
energetickými částicemi z urychlovačů.
Metastabilní
hladiny a jaderná izomerie
Doba života excitovaných jaderných hladin je většinou velmi
krátká ( »10-15-10-6 sec.), existují však situace, kdy doba života
excitované hladiny je řádově sekundy, minuty a dokonce i
několik hodin, dní i roků! - takové hladiny se nazývají metastabilní
a mluvíme o izomerním stavu jádra. Takový
jaderný izomer se často považuje sa samostatný nuklid
a označuje se horním indexem "m" u
nukleonového čísla např. 99mTc. Tento jev nastává tehdy, když v blízkosti
základního stavu jádra existuje energetická hladina, která
se od základního stavu značně liší svým momentem
hybnosti - spinem (aspoň o 3h, tj. DI ł 3), viz níže slupkový model
jádra. Potom záření g, vyslané při přechodu z takové hladiny do
základního stavu, musí mít vyšší multipolaritu (E3, M3
nebo vyšší) - přechody mezi takovými hladinami jsou málo
pravděpodobné, jsou "zakázané", takže
odpovídající doby života mohou nabývat velkých hodnot.
Izomerie a metastabilní stavy se nevyskytují u lehkých jader
(kde neexistují vzbuzené hladiny s DI ł 3), ale až u jader s nukleonovým číslem od 40;
podrobnosti vysvětluje slupkový model jádra. Důležitým
příkladem je metastabilní technecium 99mTc, které deexcituje s poločasem 6 hodin, viz
následující §1.2 "Radioaktivita", část "Záření gama".
Některé jaderné izomery však mají natolik
odlišné kvantové vlastnosti od základního stavu
(především hodnotu spinu), že nedochází k přechodu do
základního stavu emisí fotonů g-záření, ale k
radioaktivní přeměně beta-, beta+ či elektronovému záchytu, na jiné sousední jádro
(§1.2, pasáž "Jaderná izomerie a metastabilita").
Vazbová
energie atomových jader
Jak již bylo řečeno, protony a neutrony jsou v
jádře vázány přitažlivou silnou interakcí. S touto
vazbovou silou nukleonů je spojena určitá potenciální
energie zvaná vazbová energie nukleonu či
celého jádra. Pod celkovou vazbovou energií jádra
Ev se
rozumí energie potřebná k úplnému rozložení jádra na
jednotlivé volné nukleony *). Tato vazbová energie je
zároveň rovna energii, která by se uvolnila při vzniku jádra
z jednotlivých nukleonů.
*) Necháváme zde zatím stranou mechanismy, jakými lze takové
rozložení či složení jader uskutečnit; budeme se tím
zabývat v §1.3 "Jaderné reakce a
jaderná energie".
Podle relativistické koncepce ekvivalence
hmotnosti a energie je vlivem vazbové energie celková hmotnost
jádra m(Z,N) vždy poněkud menší než
součet hmotností jeho volných protonů Z.mp a neutronů (N-Z).mn. Rozdíl mezi
výslednou klidovou hmotností jádra a celkovou klidovou
hmotností volných nukleonů, z nichž je jádro složeno,
Dm =
Z.mp +
(N-Z).mn -
m(Z,N) ,
se nazývá hmotnostní úbytek či defekt.
Podle Einsteinova vztahu ekvivalence mezi hmotností a energií
souvisí hmotnostní úbytek s celkovou vazbovou energií jádra
vztahem Ev
ş DE = Dm . c2. Jestliže vydělíme
celkovou vazbovou energii jádra Ev počtem nukleonů N, dostaneme průměrnou vazbovou
energii na jeden nukleon `Ev = Ev/N.
Hmotnostní úbytek se vyjadřuje buď v gramech nebo v
atomových jednotkách hmotnosti (1/12 hmotnosti atomu uhlíku 12C), vazbová energie
se v jaderné fyzice většinou vyjadřuje v megaelektronvoltech
[MeV]. Např. jádro hélia 4He2 má hmotnostní
úbytek Dm = 0,5061.10-25g, vazbovou energii Ev ş DE = 28 MeV, na jeden nukleon připadá vazbová energie
7 MeV.
Někdy se míra hmotnostního úbytku vyjadřuje pomocí tzv. koeficientu
stěsnání d = (Dm/m), někdy násobený 10000.
Vazbová energie na jeden nukleon (či
koeficient stěsnání) s protonovým číslem zpočátku rychle
roste, největší je pro jádra kolem železa, pak zase mírně
klesá - viz obr.1.3.3 v §1.3 "Jaderné reakce a jaderná energie". Tato závislost je též rozhodující pro
možnosti získávání jaderné energie.
Obr.1.3.3 si pro názornost uvedeme i zde :
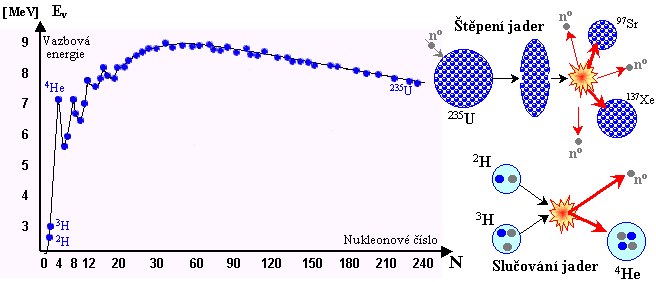
Obr.1.3.3. Závislost střední vazbové
energie Ev
jednoho nukleonu na nukleonovém čísle jádra. V počáteční
části grafu je měřítko na vodorovné ose poněkud
roztaženo, aby byly lépe vidět rozdíly vazbové energie u
nejlehčích jader. Pravá část obrázku se týká dvou
způsobů uvolnění vazbové jaderné energie, které budou
podrobně rozebírané v §1.3 "Jaderné reakce a jaderná energie"
Vazbová energie a
stabilita atomových jader
Podobně jako u jiných vázaných systémů, lze očekávat, že
vazbová energie atomových jader bude úzce souviset s jejich stabilitou.
Souvisí jednak se stabilitou "vnější" při
dodání energie jádru zvenčí (většinou rozptylem nějakých
částic ostřelujících jádro), jednak s "vnitřní"
stabilitou či nestabilitou působením vnitřních mechanismů v
nukleonech a jejich vazbách. V následujícím §1.2 "Radioaktivita" se seznámíme s procesy a mechanismy, kterými
mohou jádra přecházet z konfigurací s vyšší energií na
konfigurace s nižší energií při radioaktivních
přeměnách. Pro uskutečnění každého jaderného
procesu (a ostatně každého fyzikálního proces vůbec) musí
být splněny dvě základní podmínky: energetická
bilance a existence příslušného mechanismu,
jakým proces probíhá. O stabilitě lehčích a středně
těžkých jader rozhoduje poměr počtu protonů a
neutronů. Podle obr.1.1.10 jsou tím dány kvantové energetické
hladiny protonů a neutronů v poli jaderných sil,
které se obsazují nezávisle. Pokud v těchto hladinách
nastane situace, kdy energie jiné konfigurace protonů a
neutronů je energeticky dostatečně nižší,
"zapracuje" mechanismus slabé interakce,
která je schopna vzájemně přeměňovat protony a neutrony -
dojde k radioaktivní přeměně beta (beta- nebo
beta+
podle toho, zda je přebytek neutronů nebo protonů). Pro
těžká jádra v oblasti uranů a transuranů pak nastává radioaktivita
alfa v důsledku neschopnosti silné interakce, díky
krátkému dosahu, udržet pohromadě tak velký počet
nukleonů. Všechny tyto procesy si v §1.2
"Radioaktivita" rozebereme z hlediska mechanismů i
energetické bilance na 3-rozměrné tabulce nuklidů, mapující
i vazbové energie nukleonů v jádrech - část "Stabilita a nestabilita atomových jader", obr.1.2.8 a 1.2.9 v §1.2.
Modely atomového jádra
Vzhledem ke své velikosti »10-13cm a kvantovému charakteru jsou atomová jádra zcela
mimo možnosti jakéhokoli přímého pozorování. Pro
pochopení různých dějů s atomovými jádry je třeba si
vytvořit určité aspoň přibližné představy o jádrech a
jejich vnitřním uspořádání. Modely
atomových jader jsou určitá schématická znázornění,
fiktivní konstrukce a analogie, které s menším či větším
úspěchem vysvětlují určité vlastnosti nebo procesy u
lehkých a těžkých atomových jader. Existuje několik
modelů, z nichž každý zpravidla dobře vysvětluje jen
některé konkrétní jaderné procesy, pro něž byl vytvořen
(výjimku tvoří slupkový model, který je obecnější). Zde
se jen stručně zmíníme o někerých častěji používaných
modelech :
Různorodost atomových jader
V současné době je známo více asi 2600 druhů různých
jader, lišících se od sebe počtem protonů nebo neutronů. Z
toho stabilních jader je si 270, ostatní
jádra jsou radioaktivní. V pozemské
přírodě se vyskytuje 340 nuklidů - 270 stabilních a 70
radioaktivních. Vyjmenujme si některá důležitá konkrétní
jádra prvků.
Nejlehčím a nejjednodušším prvkem je vodík
1H1 (hydrogenium), jehož
jádro sestává jen z jediného protonu p+, kolem něhož obíhá jediný elektron e-.
Přidáním jednoho neutronu no vzniká jádro těžkého vodíku 2H1
- deuteria. Nejtěžším isotopem vodíku v přírodě
je tritium 3H1,
obsahující proton a 2 neutrony; dva neutrony na jeden proton
jsou zde však "trochu moc", rovnovážná konfigurace
je porušena a tritium 3H1
se již radioaktivně rozpadá (rozpadem b- s
poločasem 12,6 let na hélium 3). Dalším
důležitým lehkým jádrem je hélium 4He2 obsahující dva
protony a dva neutrony (v přírodě se vyskytuje i nepatrné
množství 3He).
Neexistence
stailního diprotonu a dineutronu
Nejjednodušším jádrem hélia by teoreticky měly být dva
protony (bez neutronů), svázané silnou interakcí - tzv. diproton
2He2. Diproton však v
naší přírodě neexistuje, je velice
nestabilní. Nestabilita a faktická neexistence
diprotonu má tři příčiny: 1.
Odpudívá elektrická síla
dvou stejnojmenně nabitých protonů. To však není hlavní
příčina, neboť elektromagnetická interakce je na
měřítcích 10-13cm mnohonásobně slabší než silná jaderná
interakce. 2. Kvantové relace neurčitosti vedoucí k
Pauliho vylučovacímu principu, podle nichž dvě stejné
částice nemohou být ve stejném kvantovém stavu, v tomto
případě se musí lišit opačnou orientací spinu. 3. Spinová
závislost silné jaderné interakce mezi nukleony (viz
výše pasáž "Spinová
závislost silné jaderné interakce"), která je zbytkovým projevem silné interakce
mezi kvarky uvnitř. Jaderná interakce je nejsilnější tehdy,
když jsou spiny obou nukleonů souhlasně orientovány. A to zde
není. Takže silná jaderná interakce
není schopna dostatečně přitáhnout a spojit do
stabilní konfigurace dva protony.
Podobně neexistuje ani stabilní vázaný stav
dvou neutroů - dineutron. Elektrická odpudivá
síla zde sice není, ale spinová závislost zmíněná výše v
bodu 2. a 3. se zde rovněž
uplatňuje. Přitažlivost silné interakce je zde proto též
menší a (hraničně)
nestačí ke svázání dvou neutronů k sobě. I kdyby se
hypoteticky podařilo navázat diproton či dineutron, byly by
nestabilní v důsledku slabé interakce - radioakktivity beta+ a
beta- ........
Vzájemné termojaderné reakce
dvou protonů však v obrovském rozsahu probíhají ve hvězdách,
kde jsou prvním krokem v proton-protonovém řetězci,
který je základním procesem tvorby energie ve hvězdách (je
podrobněji rozebíráno v §4.1, "Gravitace a
evoluce hvězd", část "Evoluce
hvězd" monografie "Gravitace,
černé díry a fyzika prostoročasu".
Odhaduje se, že ve středně velkých hvězdách hlavní
posloupnosti se v každém okamžiku vyskytuje cca 1038 jaderně
interagujících diprotonů!
Z dalších význačných
jader můžeme jmenovat uhlík 12C6,
dusík 14N7, kyslík 16O8, sodík 13Na11, síru 33S16, ....., železo 56Fe26, ...., zlato 197Au79 atd. Čím těžší
jádro, tím více má různých isotopů, z nichž jen některé
jsou stabilní, ale většina je radioaktivních. Posledními
stabilními jádry jsou olovo 208Pb82 a vizmut 209Bi83; všechna těžší jádra jsou již radioaktivní -
dostáváme se postupně do oblasti jader uranových (235,238U92 a další isotopy) a
transuranových (plutonium, americium, kalifornium, einsteinium,
fermium, mendělejevium ...). Nejtěžší známá jádra (jako
je 258Lw103 a vyšší) se již
rozpadají natolik rychle po jejich umělém vyrobení, že je
obtížné jejich existenci vůbec prokázat. O přípravě a
vlastnostech transuranů se podrobněji zmiňujeme v §1.3
"Jaderné reakce", část "Transurany". Vlastnosti všech důležitých jader jsou
podrobně rozebírány v §1.4 "Radionuklidy".
Stabilita atomových jader
Časová stabilita či nestabilita atomových jader je dána
složitou souhrou silných, elektromagnetických
a slabých interakcí mezi nukleony (a dokonce i
uvnitř nukleonů). V zásadě jsou jádra držena pohromadě ve
stabilní konfiguraci převahou silné přitažlivé jaderné
interakce nukleonů nad slabší odpudivou silou elektrickou mezi
protony. U příliš velkých jader silná jaderná interakce,
vzhledem ke svému krátkému dosahu, nestačí dostatečně
silně vázat jádro, což může vést k emisi nukleonů (radioaktivita
alfa), nebo dokonce k rozštěpení jádra. Uvnitř
samotných nukleonů pak působí silné a slabé interakce mezi
kvarky; ty slabé interakce mohou vést k transmutacím kvarků
uvnitř nukleonů a tím i k vzájemné přeměně mezi protony a
neutrony - to vyústí v nestabilitu jádra, v jeho přeměnu na
jiné jádro (radioaktivita beta). Mechanismy různých
druhů radioaktivity se budeme zabývat v §1.2 "Radioaktivita".
Silné, elektromagnetické a slabé interakce determinují energetické
poměry v jádře podle počtu protonů a neutronů,
jejich vzájemného poměru a uspořádání. Z energetického
hlediska si příčiny nestability jader budeme analyzovat v
§1.2, části "Stabilita a
nestabilita atomových jader".
Vznik
atomových jader a původ prvků
- jsme potomky hvězd !
Kosmická
alchymie
D.I.Mendělejev a jeho
následovníci provedli systemizaci jednotlivých prvků
známých v přírodě do periodické tabulky. Chemikové velmi
podrobně prozkoumali vlastnosti všech těchto prvků a jejich
sloučenin, které jsou původci pestrosti a různorodosti
světa.
Položme si však zvědavou otázku: Kde se tady
vzaly jednotlivé prvky? Jak vznikla jejich atomová
jádra? Sestrojil je, metaforicky řečeno, Bůh
"svýma rukama" již při stvoření světa - tj. vznikly
všechny prvky již při vzniku vesmíru? Nebo vznikly
až v průběhu další evoluce vesmíru?
Současná astrofyzika a kosmologie se jednoznačně přiklání
k druhé možnosti - vypracovala úchvatný "scénář"
chemického vývoje vesmíru - kosmické
nukleogeneze.
Podle standardního kosmologického modelu
se Vesmír zrodil před zhruba 13-15 miliardami let ve velmi
žhavém a hustém stavu - při tzv. "velkém
třesku" (Big Bang).
Vlastní akt vzniku vesmíru (velký
třesk) má v rámci klasické obecné teorie relativity
charakter bodové tzv. singularity s nulovým
objemem, nekonečnou křivostí prostoročasu, nekonečnou
hustotou energie. Podle kvantové teorie gravitace však
prostoročas v mikroměřítcích tzv. Planckovy-Wheelerovy
délky »10-33cm vykazuje natolik velké kvantové fluktuace geometrie
(metriky), že fluktuuje i topologie prostoročasu -
prostoročas má "pěnovitou" neustále spontánně
fluktuující mikrostrukturu. Podle koncepcí kvantové
kosmologie se vesmír zrodil z kvantové prostoročasové
pěny; ba co víc - spolu s naším Vesmírem se takto
se mohlo zrodit více vesmírů! (srov. "Antropický
princip aneb kosmický Bůh").
Jednotlivé fáze vývoje vesmíru po "velkém
třesku", doprovázené rychlým rozpínáním
a chladnutím vesmíru, se rozdělují na 4
význačné etapy lišící se dominantními fyzikálními
interakcemi a procesy, které v tu dobu probíhaly (podrobně je popsáno v §5.4 "Standardní
kosmologický model. Velký třesk." knihy "Gravitace, černé díry a fyzika
prostoročasu") :
Když to zrekapitulujeme, po skončení
leptonové éry se veškerá látka vesmíru skládala pouze z vodíku
(75%) a hélia (25%). Tato situace trvala zhruba
300 000 let po celou éru záření, kdy vesmír
expandoval a teplota se snižovala. Až teplota poklesla pod cca
3000°K, udržely již atomy vodílu a hélia své elektrony -
vznikl plynný vodík a hélium, nastoupila éra látky
trvající dosud. Obaka plynu byla velice řídká, ale měla
nehomogenní strukturu. Místní zhuštěniny se vlastní
gravitací začaly smršťovat, čímž vznikly zárodky kup
galaxií a galaxií. Tam gravitační smršťování a
zhušťování plynů pokračovalo, přičemž rostl tlak a
teplota (adiabatické stlačování).
Až teplota v nitru některých zhušťujících
se oblaků dosáhla cca 107 stupňů, kinetická energie jader začala překonávat
odpudivé elektrické síly mezi kladně nabitými jádry -
došlo k zapálení termonukleárních reakcí. Termonukleární
reakce je slučování atomových jader za vysokých
teplot, přičemž z lehčích jader vznikají jádra těžší
(§1.3). Vysoká teplota je potřeba k tomu, aby kladně nabitá
jádra svou kinetickou energií překonala elektrické
(Coulombovské) odpudivé síly a mohla se vzájemně
přiblížit na vzdálenost »10-13cm, kde díky přitažlivým silným interakcím mohou
obě jádra splynout a sloučit se za uvolnění značně velké
vazbové energie. Tato uvolněná energie je pak zdrojem světla
a tepla hvězdy a další smršťování se zastaví -
gravitační síly jsou vyváženy tlakem záření a tepelným
pohybem ionizovaného plynu v důsledku uvolňované jaderné
energie.
Termonukleární reakce a
nukleosyntéza ve hvězdách
(podrobnější analýza je v §4.1 "Gravitace a
evoluce hvězd", část "Evoluce
hvězd"-
"Termonukleární reakce v nitru hvězd" monografie
"Gravitace, černé díry a fyzika prostoročasu")
Po
většinu života hvězdy probíhá termojaderné
slučování vodíku na hélium, které je energeticky
nejvydatnější. Po spotřebování vodíku v nitru hvězdy na
nějakou dobu převáží gravitace, hvězda se dále smrští a
tlak a teplota stoupne natolik, že se jádra hélia začnou
slučovat na uhlík (4He
+ 4He ® 8Be + g ,8Be + 4He ® 12C + g , reakce 3a(=4He )® 12C+g ). Po vyčerpání hélia
nastává další smršťování nitra hvězdy a za stále
rostoucích teplot nastupují další termonukleární reakce
doprovázené spalováním uhlíku (např. 12C + a ® 16O + g, 16O + a ® 20Ne + g, 20Ne + a ® 24Mg +
g, 12C + 12C ® 24Mg, etc . ..) a při vyšších teplotách i kyslíku (16O + 16O ® 24Si+ a, resp. ® 31P + p, resp. ® 32S + g). Jádra křemíku a dalších prvků v horké
termonukleární plasmě zachycují neutrony, protony a a-částice, čímž
vznikají další těžší prvky. Množstvím podobných
jaderných reakcí vzniká kromě uhlíku postupně kyslík,
dusík, ..., hořčík, ..., ...křemík, ... vápník, ...
chrom, ... a nakonec železo.
Pozn.: K tomu, aby hvězda mohla
syntetizovat těžší prvky, musí mít dostatečnou hmotnost,
aby gravitace vyvolala v jejím nitru dostatečně vysoké tlaky
a teploty. Malé hvězdy dokáží vytvořit z vodíku jen
hélium, hmotnější hvězdy jako naše Slunce vytvoří jádra
až po hořčík, u podstatně větších hvězd pak proběhne
celá posloupnost termonukleárních reakcí.
Jak se termonukleárně vytvořené
těžší prvky dostanou z hvězd ven ?
Kdyby ve hvězdách neprobíhaly žádné jiné procesy kromě
termonukleární nukleosyntézy, všechny takto
"uvařené" těžší prvky by silnou gravitací
zůstaly navždy uvězněné v nitru hvězd a
nijak by nepřispěly k chemickému vývoji vesmíru, nemohl
by vzniknout ani život. Jsou naštěstí dva procesy,
které syntetizované těžší prvky uvolňují z gravitačního
sevření hvězd a obohacují nimi okolní mezihvězdný prostor
:
--> Termoemise plynů z
horních vrstev "atmosféry" hvězd - hvězdný
vítr (viz pasáž "Hvězdný
vítr"),
který průběžně odnáší do okolního prostoru malé
množství plynu hvězdy, s příměsí syntetizovaných
těžkých prvků.
--> Výbuch supernovy, který
do okolního vesmíru vyvrhne podstatné množství materiálu
hvězdy, včetně velkého množství termonuleárně
syntetizovaných prvků. A během vlatního výbuchu vytvoří i
mnoho dalších ještě těžších prvků (viz část "Výbuch supernovy. Neutronová
hvězda. Pulsary." v
§4.2).
U jader železa posloupnost termonukleárních
reakcí končí, protože prvky kolem železa mají nejvyšší
vazbovou energii, takže jaderná syntéza těžších prvků
již není exotermickou reakcí (energie se musí naopak dodat).
Všechny jaderné reakce uvolňující energii ustanou, doba
aktivního života hvězdy končí - nastává konečná
fáze hvězdné evoluce.
Co se stane dál? To záleží na zbylé hmotnosti hvězdy.
Pokud tato hmotnost není vyšší než asi 1,25 hmotností
Slunce, zůstává hvězda (stlačená gravitací z původních
několika set tisíc kilometrů do průměru několika tisíc
kilometrů a hustoty řádu tisíců kilogramů na cm3) v rovnovážném
stavu, kdy gravitační síly jsou vyváženy tzv. Fermiho
tlakem degenerovaného elektronového plynu v plně
ionizované látce. Hvězda v tomto stavu se nazývá bílý
trpaslík (dokud září rozžhavena zbylým teplem;
posléze se stává černým trpaslíkem); pro chemický
vývoj vesmíru nemá taková hvězda valný význam - těžší
prvky syntetizované během její evoluce zůstávají
gravitačně "uvězněné" v nitru bílého trpaslíka
a do okolního vesmíru se nedostanou.
Pokud má hvězda zbylou hmotnost vyšší než asi 1,25
hmotností Slunce (tzv. Chandrasekharova mez), není
již tlak elektronového plynu schopen vyvážit tak obrovské
gravitační síly, gravitace zvítězí a smršťování bude
pokračovat. Elektrony jsou "vtlačovány" do jader a
jimi pohlcovány (dochází k masívnímu
elektronovému záchytu); slučují se tam s protony za vzniku neutronů
a vylétajících neutrin: e- + p+ ® no + n
(inverzní b-rozpad). Tím se obsah elektronů ve hvězdě zmenšuje
a jejich Fermiho tlak klesá, čímž se látka hvězdy stává
snadněji stlačitelnou - dochází k dalšímu smršťování a
pohlcování elektronů. Proces pokračuje s lavinovitě
narůstající rychlostí: během zlomku sekundy dojde k
prudkému smrštění (jakési "implozi") hvězdy, při
němž se téměř všechny protony a elektrony sloučí na
neutrony (atomová jádra se rozplynou a přestanou existovat). V
tomto stádiu pak může (ale nemusí!) opět nastat rovnováha -
vznikne neutronová hvězda, která má průměr
jen několik desítek kilometrů a je složena z neutronové
"látky" s hustotou »1014g/cm3 stejného řádu jako je hustota v atomových jádrech.
Gigantické gravitační síly jsou
vyváženy Fermiho tlakem degenerovaného neutronového
"plynu". Rychle rotující neutronové hvězdy jsou ve
vesmíru pozorovány jako tzv. pulzary - vysílají
totiž při své rotaci kužel směrovaného elektromagnetického
záření, které podobně jako u majáku pozorujeme jako velmi
pravidelné rychlé záblesky záření.
Při implozi vedoucí ke vzniku neutronové hvězdy dochází
k náhlému uvolnění velkého množství energie, které se
částečně vyzáří neutriny a elektromagnetickým zářením
(nejen infračerveným a viditelným světlem, ale hlavně
tvrdým rtg a gama zářením), přičemž vnější vrstvy
hvězdy se prudce rozpínají do prostoru a vytvářejí posléze
zářící mlhovinu: vznik neutronové hvězdy je doprovázen výbuchem
supernovy, při níž je vyzářeno obrovské množství
energie a vnější vrstvy hvězdy jsou "rozmetány" do
okolního prostoru.
Pokud má vyhořelá hvězda zbylou
hmotnost více jak dvojnásobnou než je hmotnost Slunce, jsou
gravitační síly již tak velké, že překonají i Fermiho
síly mezi neutrony, katastrofální gravitační kolaps se
nezastaví ve stádiu neutronové hvězdy a pokračuje dál, až
se hvězda podle obecné teorie relativity dostane pod svůj
gravitační poloměr, překročí horizont a vznikne černá
díra (podrobnosti v kapitole 4 "Černé díry" knihy "Gravitace, černé díry a fyzika
prostoročasu").
Výbuch supernovy má pro chemický vývoj vesmíru zásadní význam, a to ve dvou směrech :
Takové hvězdy jako je naše Slunce a
celá sluneční soustava vznikly z oblaků plynů
"přetavených a převařených" dřívějšími
pokoleními hvězd *); tato oblaka byla již obohacena o těžké
prvky.
*) Hvězdy první generace, které vznikaly v období cca 300-700
tisíc let po velkém třesku z vodíku a hélia (jiné prvky
tehdy ještě ve vesmíru nebyly), měly pravděpodobně značně
velké hmotnosti cca 100-300 M¤. Podle zákonitostí hvězdné evoluce se
tedy vyvíjely velice rychle - po zhruba 3-5 milionech let
vybuchovaly jako supernovy a vnesly do mezihvězdné hmoty
těžší prvky, které v nich termonukleární syntézou
vznikly. Další generace hvězd, které vznikaly z této látky
obohacené o těžší prvky, již nedosahovaly takových
hmotností a jejich doba života byla stamiliony let až několik
miliard let. Naše Slunce vzniklo patrně až jako hvězda 3.generace z materiálu, obohaceného po výbuchu
hvězd 2.generace (a předtím 1.generace).
Hvězdy lze označit za jakési "alchymistické kotle" vesmíru, v nichž se z lehčích prvků
termonukleární synthézou vytvářejí těžší prvky.
Alchymisté, kteří se často po nocích s nábožnou úctou
dívali na hvězdy (zabývali se též astrologii), vzývali je a prosili o pomoc, naprosto netušili, že
tyto hvězdy již miliardy let před nimi dělaly (a stále
dělají) v obrovských měřítcích to, oč se oni v malých
měřítcích neúspěšně snažili - transmutace
- přeměny prvků. S trochou nadsázky lze tedy hrdě
prohlásit, že "všichni
jsme potomky hvězd!" -
každý atom uhlíku, kyslíku, dusíku, síry atd. v našem
těle vznikl kdysi dávno před miliardami let v "ohnivé
nukleární peci" nitra staré hvězdy, nyní již dávno
zaniklé. Všechny prvky na Zemi, kromě vodíku který je
prvotní a hélia, pocházejí z "prachu" hvězd
vyhořelých dávno před vznikem naší Sluneční soustavy.
Jsme "popelem" - jakýmsi "recyklovaným
odpadem" termojaderné fúze dávných hvězd...
Určitou výjimkou jsou lehké prvky deuterium, litium,
berilium a bór, které nejsou přímým produktem
termonukleárních reakcí ve hvězdách (při těchto reakcích
jsou naopak "spalovány"), ale vznikly interakcí
kosmického záření s ostatními jádry, především uhlíku,
dusíku a kyslíku, které jsou vysokoenergetickým kosmickým
zářením tříštěny na lehčí jádra.
Splynutí
neutronových hvězd
Další způsob vytváření těžších prvků ve vesmíru
nastává při těsném oběhu dvou neutronových hvězd
a jejich sloučení - splynutí, "srážka". Při tomto
procesu je vyvrženo velké množství neutronové hmoty,
která okamžitě "nukleonizuje"
za vzniku atomových jader (§4.8, pasáž "Srážky a splynutí
neutronových hvězd")
. Přitom vzniká velké množství jader, s relativně vyšším
zastoupením těžkých prvků. Vzhledem k
obrovskému množství neutronů intenzívně probíhá r-proces
rychlého opakovaného neutronového záchytu
lehčími jádry, při němž. účinně vznikají i velmi
těžká jádra - z oblasti kolem iridia, platiny, zlata, až ke
skupině uranů.
Evoluce hvězd z hlediska relativistické astrofyziky je podrobněji popsána v knize "Gravitace, černé díry a fyzika prostoročasu", §4.1 "Úloha gravitace při vzniku a evoluci hvězd"; kosmická nukleosynthéza z hlediska jaderné (astro)fyziky je nastíněna v práci "Kosmická alchymie", syntetický pohled na vývoj vesmíru pak v práci "Antropický princip aneb kosmický Bůh".
Jaderná
astrofyzika ® atomová astrochemie
Lehká atomová jádra tedy vznikala podle zákonitostí
jaderné astrofyziky na počátku vesmíru primordiální
kosmologickou nukleosyntézou, těžší jádra pak
termonukleární syntézou v nitru hvězd. Tato jádra jsou
původně "holá", bez elektronových obalů -
záření gama a prudké srážky za vysokých teplot neumožní
vznik trvalého elektronového obalu, elektrony jsou z atomového
obalu okamžitě vyráženy, dochází k úplné ionizaci
atomů. K žádným chemickým reakcím a tvorbě sloučenin zde
nemůže docházet. Ve vyvrhnutých oblacích se tato jádra
dostanou do chladného mezihvězdného prostoru, kde si jádra
svou elektrickou přitažlivostí zachytí volné elektrony,
kterými zaplní elektronové orbity a vzniknou tak úplné
atomy prvků. Mezi nimi již může docházet k
chenickým reakcím.
Pravděpodobnost srážky a sloučení dvou či více atomů
v řídkém plynném skupenství chladných mezihvězdných
oblaků je velmi malá. Existují však dva důležité
mechanismy chemických reakcí ve vesmíru:
¨ "Studená"
astrochemie
Pro vznik molekul z atomů ve vesmíru jsou velmi důležité
pevné prachové částice, zkondenzované ve vyvržené
mlhovině. Tam jsou atomy navzájem blízko a mohou si
vyměňovat elektrony - chemické reakce a syntéza
molekul z atomů v mezihvězdném prostoru probíhají
na zrnkách prachu. Mohou být stimulovány i
zářením z okolních hvězd a kosmickým zářením. Z
neutrálních atomů se interakcí se zářením stávají ionty,
které díky přitažlivým elektrickým silám jsou schopny
uskutečnit reakce a vazby do molekul i za velmi nízkých teplot
(při nichž běžné chemické reakce neprobíhají).
¨ "Horká"
astrochemie
Jako "vesmírné chemické laboratoře" mohou fungovat plynné
obálky kolem některých hvězd, především kolem
červených obrů, bohatých na uhlík a kyslík. Jsou zde velké
rozdíly teplot a tlaků v jednotlivých oblastech obálky a je
zde přítomno intenzívní záření. Kinetická energie
tepelného pohybu atomů překonává odpudivé elektrické síly
a atomy se mohou přiblížit tak, že dochází ke sdílení
valenčních elektronů a jejich slučování do molekul. Ve
vnitřní části jsou vyšší teploty a mohou zde vznikat
sloučeniny křemíku, hořčíku, hliníku, sodíku atd. Ve
vnějších částech s nižší teplotou mohou vznikat
sloučeniny s delšími uhlíkovými řetězci.
K intenzívním chemickým reakcím pak dochází v protoplanetárních
discích a z nich zformovaných planetách
kolem hvězd, kde je dostatečná hustota a často i příznivá
teplota.
Pomocí radioastronomické spektrometrie bylo v
mezihvězdných oblacích objeveno velké množství molekul
nejen anorganických (vody, oxidu uhličitého, amoniaku, ...),
ale i více jak 100 různých druhů molekul
"organických" složených z vodíku, uhlíku,
kyslíku, dusíku. Některé jsou složeny z více jak 10 atomů,
vedle metanu se vyskytují i polycyklické aromatické
uhlovodíky, aldehydy, alkoholy a pod.
Pro naši Zemi a Sluneční soustavu byl
důležitý jeden hvězdný veleobr (či několik těchto hvězd)
na vnitřní straně jednoho ze spirálních ramen Mléčné
dráhy, který před asi 7 miliardami let vybuchl jako supernova
a z jím vyvrženého oblaku, obohaceného o těžší a
biogenní prvky, pak zkondenzovala zárodečná mlhovina pro
Slunce a celou naši sluneční soustavu. Nevíme, kde se
nachází pozůstatek této předchozí hvězdy, skončil patrně
jako černá díra.
Zastoupení
prvků v přírodě
Shora nastíněná kosmická
nukleosyntéza - primordiální kosmologická a
stelární - vedla k nynějšímu průměrnému zastoupení
jednotlivých prvků ve vesmíru podle obr.1.1.12 nahoře. Daleko
nejhojnějšími prvky ve vesmíru jsou vodík a hélium. V
zásadě lze říci, že prvek se vyskytuje ve vesmíru tím
hojněji, čím menší má protonové (atomové) číslo, tedy
čím méně protonů v jádře obsahuje, čím je jednodušší
- tím snadněji vzniká v jaderných reakcích. Výjimkou jsou
lehké prvky lithium (Li), berylium (Be) a bór (B), jejichž
výrazně menší výskyt je způsoben tím, že se v nitru
hvězd "spalují" na hélium ještě předtím, než
nastupuje hlavní přeměna vodíku v hélium. Opačnou výjimkou
je skupina velmi stabilních prvků (s vysokou vazbovou energií
jader, takže snáze "přežívají" závěrečná
stádia hvězdného vývoje) kolem železa (Fe), jejichž obsah
je zvýšený. Velmi nepatrný výskyt prvků, které nemají
stabilní izotopy - technecia (Tc), promethia (Pm) a aktinidů
jako je polonium (Po) až paladium (Pa), je dán jejich
radioaktivitou s ne příliš dlouhým poločasem rozpadu; tyto
prvky mohou ve stopových množstvích vznikat záchytem
neutronů. Thorium (Th) a uran (U) jsou sice rovněž nestabilní
(radioaktivní), ale s velmi dlouhými poločasy rozpadu (řádu
108-1010let), takže se po
svém vzniku v supernovách stačí dlouhodobě zachovávat v
mezihvězdných oblacích, ve hvězdách a planetách.
Pravidelné
"oscilace" v zastoupení mezi sousedními prvky, které
jsou na grafu vidět (zvláště v oblastech mezi Z=8-20, 30-40,
45-60 a 62-75), souvisejí s poněkud vyšší vazbovou energií
jader se sudým protonovým číslem, než jader s lichým
počtem protonů. Tato sudá jádra jsou proto poněkud
stabilnější - snadněji vznikají v jaderných reakcích a
jsou "odolnější" vůči destrukci při bouřlivých
závěrečných stádiích hvězdného vývoje. Proto se
vyskytují o něco hojněji ve srovnání se svými
"lichými" sousedy.
Pozn.: Chemický vývoj vesmíru stále
pokračuje, takže nynější zastoupení prvků
se bude ve vzdálené budoucnost měnit; bude docházet
především k ubývání lehkých prvků, které budou fúzovat
na prvky těžší. Viz též §5.6 "Budoucnost
vesmíru. Šipka času. Skrytá hmota." zmíněné monografie "Gravitace, černé
díry ...".
 |
| Obr.1.1.12. Relativní zastoupení
prvků v přírodě v závislosti na jejich protonovém
(atomovém) čísle Z, vztažené k vodíku Z=1. Nahoře: Nynější průměrné zastoupení prvků ve vesmíru. Dole: Výskyt prvků na Zemi (v zemské kůře) a terestrických planetách. Vzhledem k velkému rozpětí hodnot je relativní zastoupení prvků (vztažené k vodíku Z=1) na svislé ose vyneseno v logaritmickém měřítku; to ale může zvláště na horním grafu opticky zkreslit velký rozdíl v zastoupení vodíku a hélia oproti těžším prvkům.. |
Zastoupení
prvků v přírodě - výběrové mechanismy
Základní zastoupení
jednotlivých prvků v globální "vesmírné"
přírodě je tedy dáno především primordiální
kosmologickou nukleosyntézou (viz
§5.4 "Standardní kosmologický model. Velký třesk.
Formování struktury vesmíru.",
pasáž "Prvotní nukleosyntéza") - 98% lehkých prvků vodíku a hélia
(se stopovým množstvím litia) a jen 2% těžších
prvků vytvořených nukleosyntézou v
předchozích generacích hvězd (je popsáno§4.1 " "Úloha
gravitace při vzniku a evoluci hvězd""
pasáž "Termonukleární reakce v nitru hvězd"), které v závěrečných fázích svého života tyto
hvězdy vyvrhovaly do mezihvězdného prostoru (§4.2 "Konečné fáze hvězdné evoluce.
Gravitační kolaps", část
"Výbuch supernovy, neutronové hvězdy, pulsary"). Takové je přibližné zastoupení prvků ve
stávajících hvězdách, mezihvězdné látce, mlhovinách,
plyno-prachových oblacích.
Avšak detailněji, v různých místech ve Vesmíru a v
různých časech, se může chemické složení hmoty výrazně
lišit, dochází k diferenciaci chemického složení
- uplatňují se výběrové mechanismy
"zvýhodňující" některé prvky a jiné
potlačující :
Časový výběrový
faktor
je dán mírou stability či nestability (radioaktivity) prvků.
Při výbuchu supernovy jsou vyvrženy a vznikají v zásadě všechny
isotopy všech prvků. Těsně po této grandiózní
události bychom tedy v okolí supernovy mohli nalézt nejen
stabilní prvky, ale i řadu prvků radioaktivních. Z hlediska
astronomických vzdáleností a časových měřítek se pro
další vývoj však zachovají pouze stabilní jádra
a z radioaktivních jen ty, jejichž poločas radioaktivního
rozpadu je dostatečně dlouhý, větší než
cca 108let.
Nestabilní jádra s kratším poločasem se za miliardy let po
výbuchu supernovy rozpadnou (přemění na
jiná, stabilní jádra), takže je v látce již nenajdeme.
Gravitační
výběrový faktor
způsobuje prostorovou selekci lehčích a těžších prvků - gravitační
diferenciaci hustoty, především v planetárních
soustavách kolem hvězd. Těžší prvky (jako je železo a
nikl) sesedají směrem ke středu a soustřeďují se v jádrech
planet, lehčí látky (jako jsou křemičitany) naopak
vyplouvají k povrchu - dochází k planetární diferenciaci
hustoty. Gravitace v koprodukci s tlakem záření a jeho
tepelnými účinky funguje jako "hmotnostní
separátor", oddělující lehké prvky a
molekuly od těžších v protoplanetárních discích
kolem vznikajících hvězd (§4.1 "Úloha
gravitace při vzniku a evoluci hvězd"
zmíněné monografie, část "Planety"). Ve vnitřních částech planetárních
soustav (jako je naše Sluneční soustava) proto vznikají
menší planety s vyšším obsahem těžších prvků - terestrické
planety, zatímco ve vzdálenějších oblastech
vznikají velké planety složené především z lehkých plynů
- plynní obři. Relativní
zastoupení prvků na Zemi a dalších terestrických planetách
je proto diametrálně odlišné od průměrného zastoupení
prvků ve vesmíru - viz. obr.1.1.12 dole. Hlavním rozdílem je
podstatně vyšší zastoupení těžších prvků
(vzhledem k vodíku) a praktická absence hélia (viz níže "Hélium - prvek boha Slunce").
Chemický výběrový
faktor
souvisí s různou reaktivitou prvků a s vlastnostmi
vznikajících sloučenin. Je dán především rozdílem mezi
hustými a těžko tavitelnými sloučeninami křemíku a řady
kovů, oproti těkavým sloučeninám vodíku, uhlíku a
dalších prvků. Jakož i inertními vlastnostmi hélia a
dalších "vzácných" plynů.
Vzácné
a exotické prvky v přírodě
Jak již bylo výše uvedeno, při termonukleárních reakcích v
nitru hvězd a pak při výbuchu supernovy vznikají jádra
prakticky všech prvků Mendělejevovovy
tabulky, včetně těžkých jáder až po transurany. Vznikají
přitom různé isotopy všech těchto prvků,
včetně radioaktivních. Pro další vývoj se ovšem zachovají
pouze stabilní jádra a z radioaktivních pak
ty, jejichž poločas radioaktivního rozpadu je dostatečně
dlouhý, delší než cca 108let.
Zaniklé radionuklidy
Nestabilní jádra s kratším poločasem se za miliardy let po
výbuchu naší "mateřské" supernovy již stačily rozpadnout
(přeměnit na jiná, stabilní jádra). Tyto zaniklé
radionuklidy - "vyhořelé" či
"vymřelé" - se v naší pozemské přírodě již
nevyskytují (nebo se vyskytují velmi
vzácně, pokud kontinuálně vznikají přírodními procesy
jako je kosmické záření nebo rozpadové řetězce
dlouhodobých radionuklidů - §1.4 "Radionuklidy"). Jejich dřívější existenci můžeme vyvodit z
analýzy zastoupení jejich stabilních rozpadových produktů
(dceřinných nuklidů). Příkladem je jód 129I, který se s
poločasem 15,7.106 let rozpadá na stabilní xenon 129Xe; ten byl ve zvýšené koncentraci nalezen ve
vzorcích jódu v meteoritech. Dále hliník 26Al, který se
rozpadá na hořčík 26Mg; nebo železo 60Fe .......
Z
radioaktivních jader se zachovaly tzv. primární
radionuklidy (jako je 40K, 232Th, 235,238U), i když jejich množství je nižší než na
počátku - viz §1.4 "Radionuklidy". Nezachovaly se žádné transurany, stejně jako
radioaktivní isotopy jiných prvků s poločasy kratšími než
cca 108let.
V následujícím §1.2 "Radioaktivita" budou podrobně rozebírány zákonitosti
radioaktivních přeměn. Prakticky všechny lehké a středně
těžké prvky až po vizmut (tj. s protonovým číslem menším
než 84) mají své stabilní isotopy,
zastoupené v přírodě.
Pozoruhodnou výjimkou je technecium Tc43,
které nemá stabilní izotop (nejstabilnější
je 98Tc s
poločasem 4,2 milionu let, ...); je známo asi 30 isotopů
technecia. V pozemské přírodě se proto prakticky nevyskytuje
a jeho místo v Mendělejevově periodické tabulce zůstávalo
dlouho prázdné. Uměle připravené technecium bylo poprve
nalezeno v r.1937 chemiky C.Perrierem a E.Segrém ve vzorku
molybdenu, který předtím jaderný fyzik T.Lawrence ozařoval
urychlenými jádry deuteria (docházelo přitom k reakcím 96Mo+2H®97Tc+n, resp. 98Mo+2H®97Tc+2n). Později (v
r.1962) bylo stopové množství technecia nalezeno v uranové
rudě (cca 1mg Tc na 1kg U), kde vzniká jako jeden ze
štěpných produktů při spontánním štěpení 235U. Poměrně
značné množství technecia vzniká v jaderných reaktorech
při štěpení uranu - v palivových článcích vzniká cca 27
mg Tc na každý gram rozštěpeného 235U. Vzhledem k dlouhému poločasu rozpadu patří
technecium k obtížným složkám jaderného odpadu. Je dále zajímavé, že tento
exotický a v přírodě prakticky neznámý prvek se díky
svému metastabilnímu isotopu 99mTc, který je čistým g-zářičem,
stal velmi důležitým radionuklidem, na němž je založena
většina metod tzv. radiosotopové scintigrafie
v nukleární medicíně - viz kap.4 "Scintigrafie".
Dalším takovým prvkem ze středu Mendělejevovy
periodické tabulky, který nemá stabilní isotop a proto se
vyskytuje jen v nepatrném zastoupení, je promethium
(Pm). A samozžejmě všechny prvky těžší než vizmut - aktinidy
jako je polonium, radium, radon, transurany. Thorium a uran
rovněž nemají stabilní isotopy, ale thorium-232 a
uran-238,235 se běžně vyskytují v přírodě díky svým
velmi dlouhým poločasům rozpadu (jak bylo zmíněno výše).
Hélium -
prvek boha Slunce
Za zajímavost stojí i pozemský příběh druhého
nejhojnějšího prvku ve vesmíru - hélia 4He2. V pozemské
přírodě je hélium natolik vzácné, že dlouho nebylo známé
a bylo poprvé objeveno kupodivu nikoli na Zemi, nýbrž na
Slunci! Stalo se tak r.1868, kdy francouzský astronom
Pierre Janssen podrobně zkoumal spektrum slunečního záření
a všiml si, že kromě spektrálních čar vodíku, uhlíku,
kyslíku a dalších známých prvků, jsou přítomny i
spektrální čáry dosud neznámého "slunečního"
prvku, který byl nazván hélium (Hélios =
starořecký bůh Slunce). Teprve později bylo hélium
nalezeno i na Zemi, a to nejprve v uranových rudách (r.1895
W.Ramsay, P.T.Cleve a N.A.Langley), dále
pak v zemním plynu, z něhož se nyní těží.
Proč je všeobecně hojně ve vesmíru
rozšířené hélium na Zemi tak vzácné? Je to proto, že
hélium je příliš lehký a inertní
plyn, který se s ničím neslučuje (valenční
elektrony He zcela zaplňují valenční orbital 1s a
znemožňují tak chemickou reakci s jinými prvky).
Zemská gravitace si jej neudrží, při
pozemské teplotě hélium v atmosféře stoupá vzhůru a z
horních vrstev atmosféry uniká do vesmírného prostoru.
Stejným způsobem se sice chová i plynný vodík, avšak ten
díky své vysoké reaktivitě se sloučil s kyslíkem na
těžší molekuly vody (které zemská gravitace udrží) a byl
tak na Zemi zachován ve velkém množství.
Pozn.: Pouze velké hmotné planety (jako je Jupiter) si
díky silnější gravitaci udrží v atmosféře větší
množství hélia.
Hélium tedy zůstalo na Zemi zachováno pouze v uzavřených
podzemních prostorech, odkud nemohlo uniknout do
atmosféry. Všechno toto hélium na Zemi patrně pochází z radioaktivního
a-rozpadu přírodních radioaktivních
látek, uranu a thoria - samotná a-částice je
totiž jádrem hélia, viz následující §1.2
"Radioaktivita", část "Radioaktivita alfa". Odhaduje se, že tímto způsobem v nitru Země
vzniká cca 3000 tun hélia za rok. Většina takto vzniklého
hélia zůstává nasorbována v krystalové mřížce uvnitř
hornin, část se uvolňuje v plynné fázi do dutin v zemské
kůře. Tyto uzavřené podzemní prostory jsou zároveň
zásobárnou zemního plynu, z něhož se hélium izoluje
frakční destilací a zkapalňováním (v
zemním plynu se hélium vyskytuje v koncentraci až 7%). Nejčastější použití kapalného hélia je jako chladícího
média, neboť má ze všech látek nejnižší bod varu
4,22°K = -268,9°C. Varem kapalného hélia lze dosáhnout velmi
nízkých teplot, při nichž řada vodičů vykazuje supravodivost
(§1.5
"Elementární částice", pasáž "Fermiony v úloze bosonů; Supravodivost").
Kapalné hélium se proto používá pro chlazení supravodivých
elektromagnetů (§1.5, pasáž "Elektromagnety v urychlovačích") v nukleární magnetické
rezonanci, urychlovačích, tokamacích (§1.3
"Jaderné reakce", část "Tokamak").
| Zpět: Jaderná fyzika a fyzika ionizujícího záření | |||
| Jaderná a radiační fyzika | Detekce a spektrometrie záření | Aplikace záření | |
| S c i n t i g r a f i e | Počítačové vyhodnocování scintigrafie | Radiační ochrana | |
| Gravitace, černé díry a fyzika prostoročasu | Antropický princip aneb kosmický Bůh | |||
| AstroNuklFyzika ® Jaderná fyzika - Astrofyzika - Kosmologie - Filosofie | |||